Comment effectuer un test de Breusch-Pagan dans SAS

Un test de Breusch-Pagan est utilisé pour déterminer si l’hétéroscédasticité est présente dans une analyse de régression.

Ce didacticiel explique comment effectuer un test de Breusch-Pagan dans SAS.

Exemple : test de Breusch-Pagan dans SAS

Supposons que nous souhaitions adapter un modèle de régression linéaire multiple qui utilise le nombre d’heures passées à étudier et le nombre d’examens préparatoires passés pour prédire la note finale des étudiants à l’examen :

Score de l’examen = β ₀ + β ₁ (heures) + β ₂ (examens préparatoires)

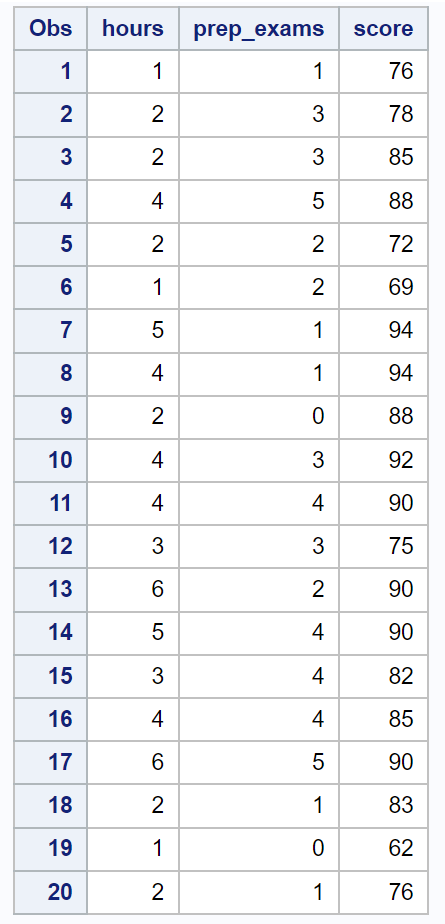
Tout d’abord, nous allons utiliser le code suivant pour créer un ensemble de données contenant ces informations pour 20 étudiants :

/*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run;

/*view dataset*/
proc print data=exam_data;

Ensuite, nous utiliserons le modèle proc pour ajuster ce modèle de régression linéaire multiple ainsi que la déclaration païenne pour effectuer le test de Breusch-Pagan pour l’hétéroscédasticité :

/*fit regression model and perform Breusch Pagan test*/
proc model data=exam_data;
    parms a1 b1 b2;
    score = a1 + b1*hours + b2*prep_exams;
    fit score / pagan=(1 hours prep_exams)
    out=resid1 outresid;
run;
quit;

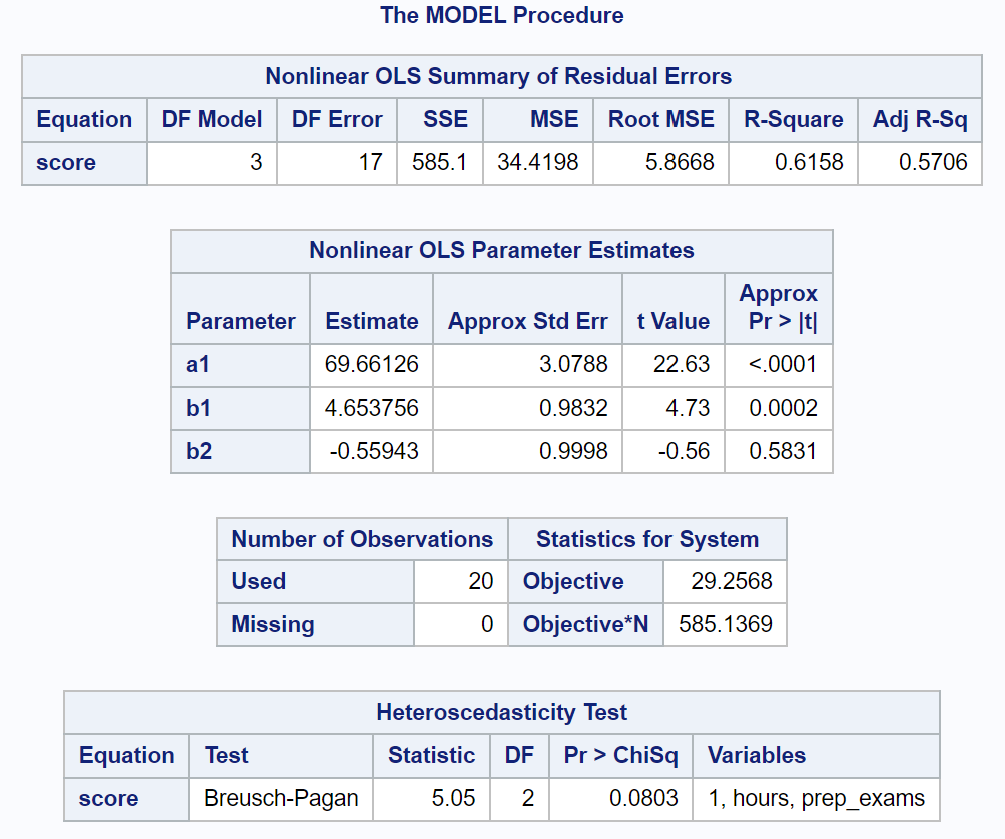
Le dernier tableau du résultat montre les résultats du test de Breusch-Pagan.

À partir de ce tableau, nous pouvons voir que la statistique du test est de 5,05 et la valeur p correspondante est de 0,0803 .

Puisque la valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.

Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer que l’hétéroscédasticité est présente dans le modèle de régression.

Il est donc possible d’interpréter en toute sécurité les erreurs types des estimations des coefficients dans le tableau récapitulatif de régression.

Que faire ensuite

Si vous ne parvenez pas à rejeter l’hypothèse nulle du test de Breusch-Pagan, alors l’hétéroscédasticité n’est pas présente et vous pouvez procéder à l’interprétation du résultat de la régression originale.

Cependant, si vous rejetez l’hypothèse nulle, cela signifie qu’une hétéroscédasticité est présente dans les données. Dans ce cas, les erreurs types affichées dans le tableau de sortie de la régression peuvent ne pas être fiables.

Il existe plusieurs manières courantes de résoudre ce problème, notamment :

1. Transformez la variable de réponse. Vous pouvez essayer d’effectuer une transformation sur la variable de réponse.

Par exemple, vous pouvez utiliser le journal de la variable de réponse au lieu de la variable de réponse d’origine.

Généralement , prendre le log de la variable de réponse est un moyen efficace de faire disparaître l’hétéroscédasticité.

Une autre transformation courante consiste à utiliser la racine carrée de la variable de réponse.

2. Utilisez la régression pondérée. Ce type de régression attribue un poids à chaque point de données en fonction de la variance de sa valeur ajustée.

Cela donne de petits poids aux points de données qui ont des variances plus élevées, ce qui réduit leurs carrés résiduels.

Lorsque les pondérations appropriées sont utilisées, cela peut éliminer le problème de l’hétéroscédasticité.