Comment effectuer un test Breusch-Pagan dans Stata

La régression linéaire multiple est une méthode que nous pouvons utiliser pour comprendre la relation entre plusieurs variables explicatives et une variable de réponse.

Malheureusement, un problème qui se produit souvent en régression est connu sous le nom d’ hétéroscédasticité , dans lequel il y a un changement systématique dans la variance des résidus sur une plage de valeurs mesurées.

Un test que nous pouvons utiliser pour déterminer si une hétéroscédasticité est présente est le test de Breusch-Pagan . Ce test produit une statistique de test du Chi carré et une valeur p correspondante.

Si la valeur p est inférieure à un certain seuil (les choix courants sont 0,01, 0,05 et 0,10), il existe alors suffisamment de preuves pour affirmer qu’une hétéroscédasticité est présente.

Ce tutoriel explique comment effectuer un test de Breusch-Pagan dans Stata.

Exemple : test de Breusch-Pagan dans Stata

Nous utiliserons l’ensemble de données Stata intégré automatiquement pour illustrer comment effectuer le test de Breusch-Pagan.

Étape 1 : Chargez et affichez les données.

Tout d’abord, utilisez la commande suivante pour charger les données :

utilisation automatique du système

Ensuite, affichez les données brutes à l’aide de la commande suivante :

br

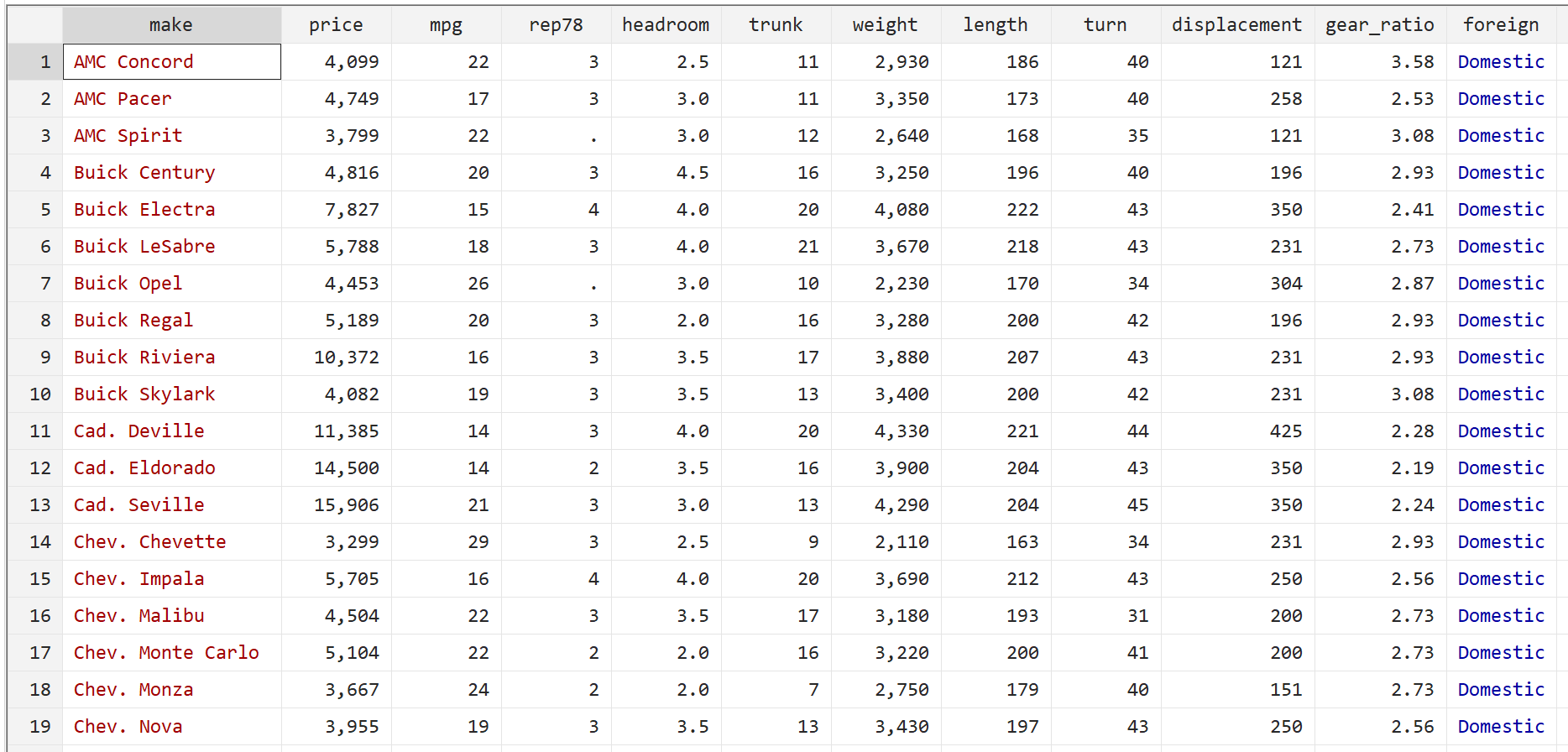
Étape 2 : Effectuez une régression linéaire multiple.

Ensuite, nous saisirons la commande suivante pour effectuer une régression linéaire multiple en utilisant le prix comme variable de réponse et le mpg et le poids comme variables explicatives :

régression prix mpg poids

Étape 3 : Effectuez le test de Breusch-Pagan.

Une fois que nous avons ajusté le modèle de régression, nous pouvons alors effectuer le test de Breusch-Pagan en utilisant la commande hettest , qui est l’abréviation de « test d’hétéroscédasticité » :

le plus chaud

Voici comment interpréter le résultat :

Ho : Il s’agit de l’hypothèse nulle du test, qui stipule qu’il existe une variance constante entre les résidus.

Variables : Cela nous indique la variable de réponse qui a été utilisée dans le modèle de régression. Dans ce cas, il s’agissait du prix variable.

chi2(1) : Il s’agit de la statistique du test du chi carré du test. Dans ce cas, il s’agit de 14h78.

Prob > chi2 : Il s’agit de la valeur p qui correspond à la statistique du test du chi carré. Dans ce cas, il s’agit de 0,0001. Cette valeur étant inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle et conclure à la présence d’hétéroscédasticité dans les données.

Que faire ensuite

Si vous ne parvenez pas à rejeter l’hypothèse nulle du test de Breusch-Pagan, alors l’hétéroscédasticité n’est pas présente et vous pouvez procéder à l’interprétation du résultat de la régression originale.

Cependant, si vous rejetez l’hypothèse nulle du test de Breusch-Pagan, cela signifie qu’une hétéroscédasticité est présente dans les données. Dans ce cas, les erreurs types affichées dans le tableau de sortie de la régression ne sont pas fiables. Il existe plusieurs façons de résoudre ce problème, notamment :

1. Transformez la variable de réponse. Vous pouvez essayer d’effectuer une transformation sur la variable de réponse. Par exemple, vous pouvez utiliser log(price) au lieu de price comme variable de réponse. Généralement, prendre le log de la variable de réponse est un moyen efficace de faire disparaître l’hétéroscédasticité. Une autre transformation courante consiste à utiliser la racine carrée de la variable de réponse.

2. Utilisez la régression pondérée. Ce type de régression attribue un poids à chaque point de données en fonction de la variance de sa valeur ajustée. Essentiellement, cela donne de faibles poids aux points de données qui ont des variances plus élevées, ce qui réduit leurs carrés résiduels. Lorsque les pondérations appropriées sont utilisées, cela peut éliminer le problème de l’hétéroscédasticité.

3. Utilisez des erreurs standard robustes. Les erreurs types robustes sont plus « robustes » au problème de l’hétéroscédasticité et tendent à fournir une mesure plus précise de la véritable erreur type d’un coefficient de régression. Consultez ce didacticiel pour savoir comment utiliser des erreurs standard robustes en régression dans Stata.