Test d’ajustement du chi carré sur une calculatrice TI-84
Un test d’ajustement du chi carré est utilisé pour déterminer si une variable catégorielle suit ou non une distribution hypothétique.
Ce didacticiel explique comment effectuer un test d’ajustement du chi carré sur une calculatrice TI-84.
Exemple : test d’ajustement du chi carré sur une calculatrice TI-84
Un propriétaire de magasin affirme qu’un nombre égal de clients viennent dans son magasin chaque jour de la semaine. Pour tester cette hypothèse, un chercheur indépendant enregistre le nombre de clients qui viennent dans le magasin au cours d’une semaine donnée et constate ce qui suit :
- Lundi : 50 clients
- Mardi : 60 clients
- Mercredi : 40 clients
- Jeudi : 47 clients
- Vendredi : 53 clients
Nous utiliserons les étapes suivantes pour effectuer un test d’ajustement du chi carré afin de déterminer si les données sont cohérentes avec l’affirmation du propriétaire du magasin.
Étape 1 : Saisissez les données.
Tout d’abord, nous saisirons les valeurs des données pour le nombre attendu de clients chaque jour et le nombre observé de clients chaque jour. Appuyez sur Stat puis appuyez sur EDIT . Saisissez les valeurs suivantes pour le nombre de clients observé dans la colonne L1 et les valeurs pour le nombre attendu de clients dans la colonne L2 :
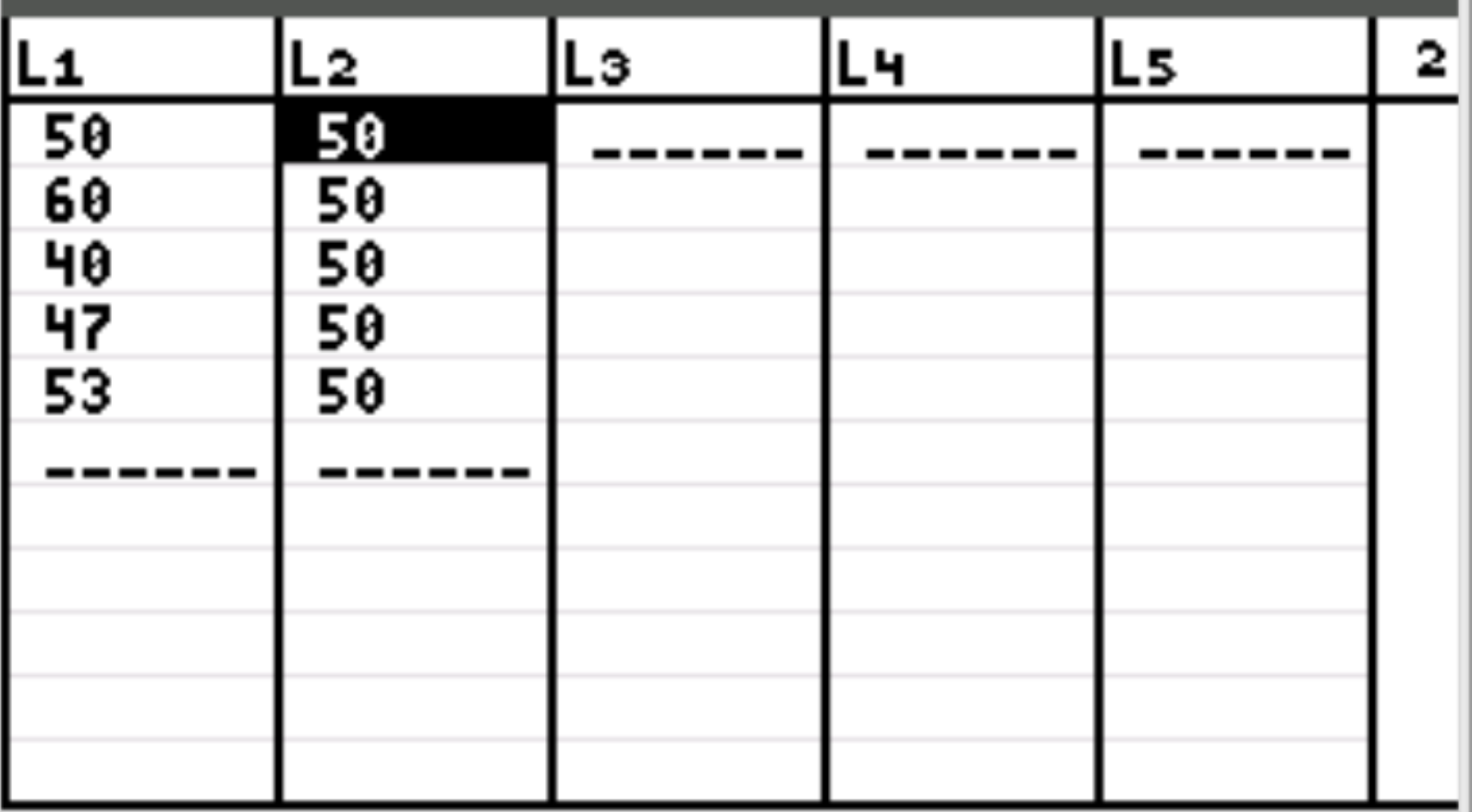
Remarque : Il y avait 250 clients au total. Ainsi, si le propriétaire du magasin s’attend à ce qu’un nombre égal de clients entre dans le magasin chaque jour, cela représenterait 50 clients par jour.
Étape 2 : Effectuez le test d’ajustement du chi carré.
Ensuite, nous effectuerons le test d’ajustement du chi carré. Appuyez sur Stat puis faites défiler jusqu’à TESTS . Faites ensuite défiler jusqu’à X 2 GOF-Test et appuyez sur Entrée .
Pour Observed , choisissez la liste L1. Pour Expected , choisissez la liste L2. Pour df (degrés de liberté), entrez # catégories – 1. Dans notre cas, nous avons 5-1 = 4. Mettez ensuite en surbrillance Calculer et appuyez sur Entrée .
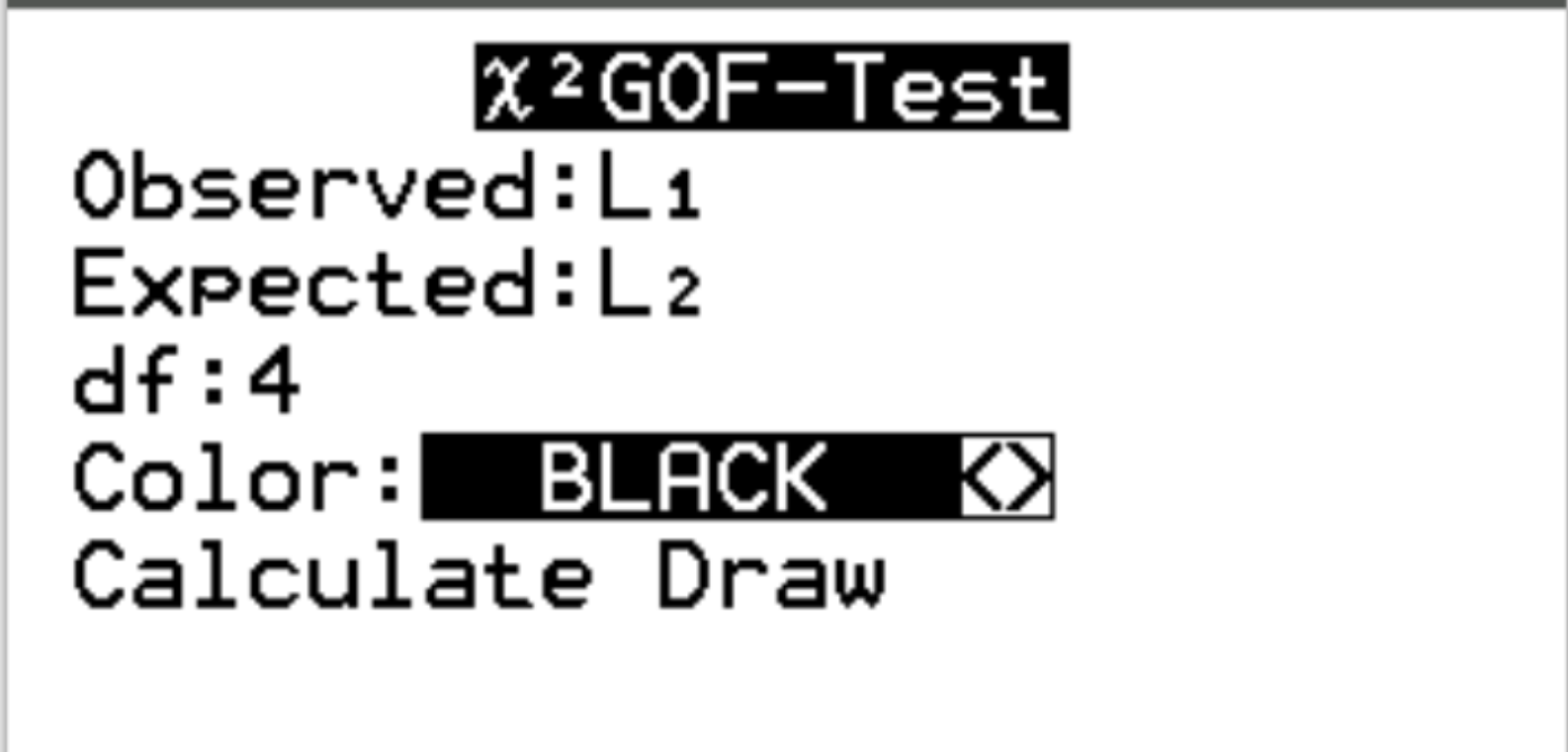
La sortie suivante apparaîtra automatiquement :
Étape 3 : Interprétez les résultats.
La statistique du test X 2 pour le test est de 4,36 et la valeur p correspondante est de 0,3595 . Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Cela signifie que nous n’avons pas suffisamment de preuves pour affirmer que la véritable répartition des clients est différente de celle déclarée par le propriétaire du magasin.
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus