Comment effectuer une régression linéaire sur une calculatrice TI-84
La régression linéaire est une méthode que nous pouvons utiliser pour comprendre la relation entre une variable explicative, x, et une variable de réponse, y.
Ce didacticiel explique comment effectuer une régression linéaire sur une calculatrice TI-84.
Exemple : régression linéaire sur une calculatrice TI-84
Supposons que nous souhaitions comprendre la relation entre le nombre d’heures qu’un étudiant étudie pour un examen et la note qu’il obtient à l’examen.
Pour explorer cette relation, nous pouvons effectuer les étapes suivantes sur une calculatrice TI-84 pour effectuer une régression linéaire simple en utilisant les heures étudiées comme variable explicative et la note d’examen comme variable de réponse.
Étape 1 : Saisissez les données.
Tout d’abord, nous saisirons les valeurs des données pour la variable explicative et la variable de réponse. Appuyez sur Stat puis appuyez sur EDIT . Entrez les valeurs suivantes pour la variable explicative (heures étudiées) dans la colonne L1 et les valeurs pour la variable de réponse (score à l’examen) dans la colonne L2 :
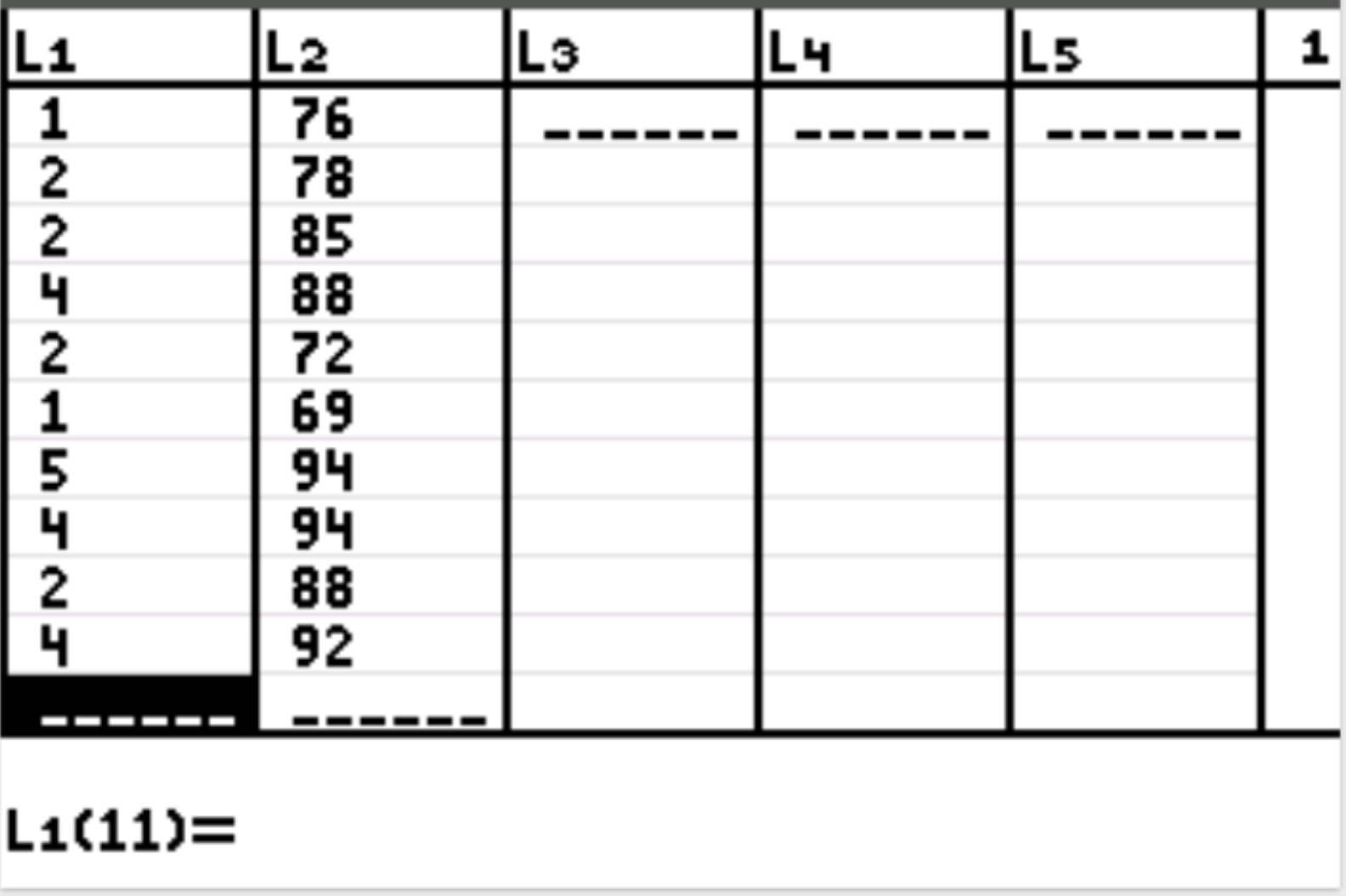
Étape 2 : Effectuez une régression linéaire.
Ensuite, nous effectuerons une régression linéaire. Appuyez sur Stat puis faites défiler jusqu’à CALC . Faites ensuite défiler jusqu’à 8 : Linreg(a+bx) et appuyez sur Enter .
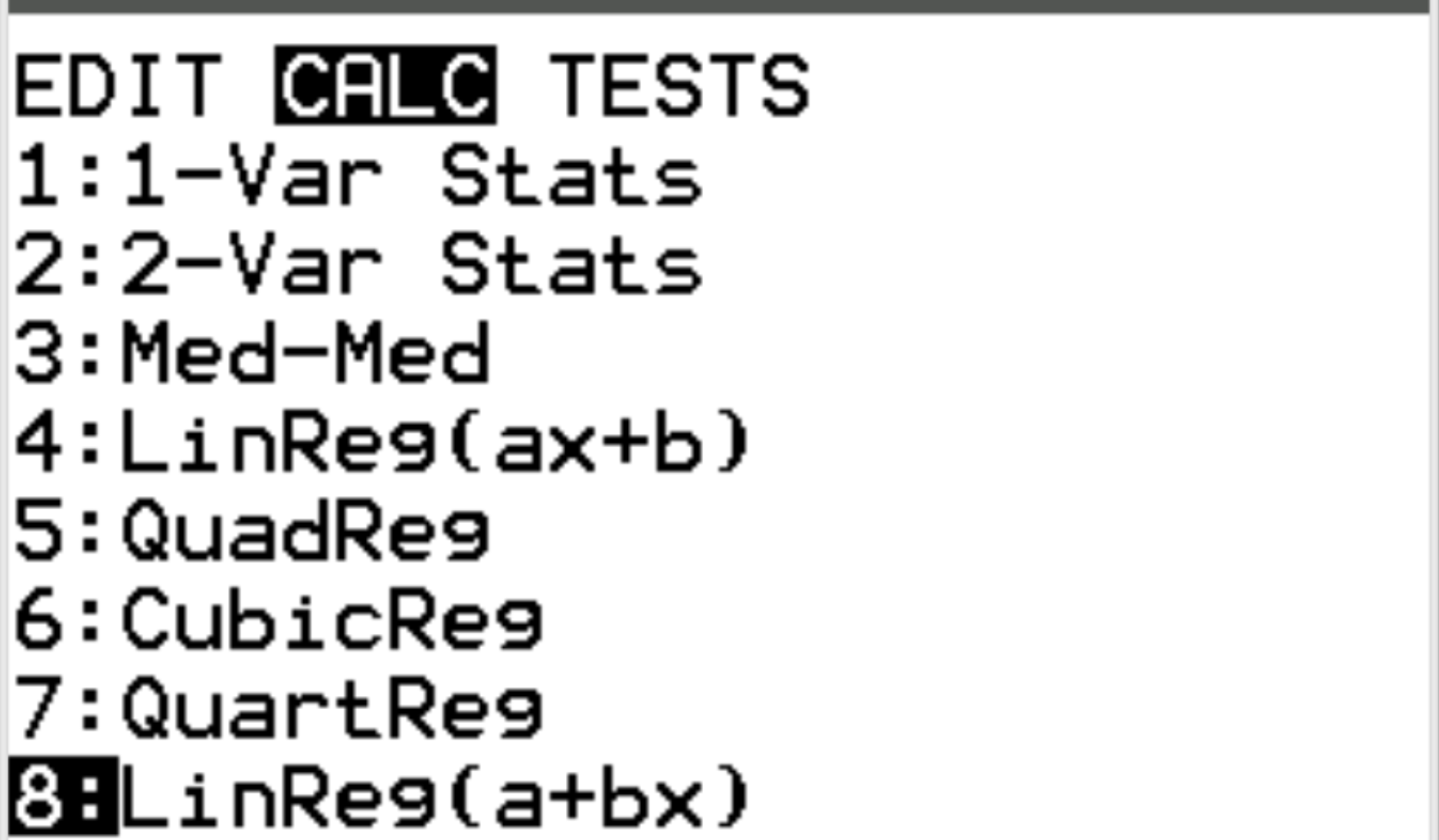
Pour Xlist et Ylist, assurez-vous que L1 et L2 sont sélectionnés car ce sont les colonnes que nous avons utilisées pour saisir nos données. Laissez FreqList vide. Faites défiler jusqu’à Calculer et appuyez sur Entrée . La sortie suivante apparaîtra automatiquement :
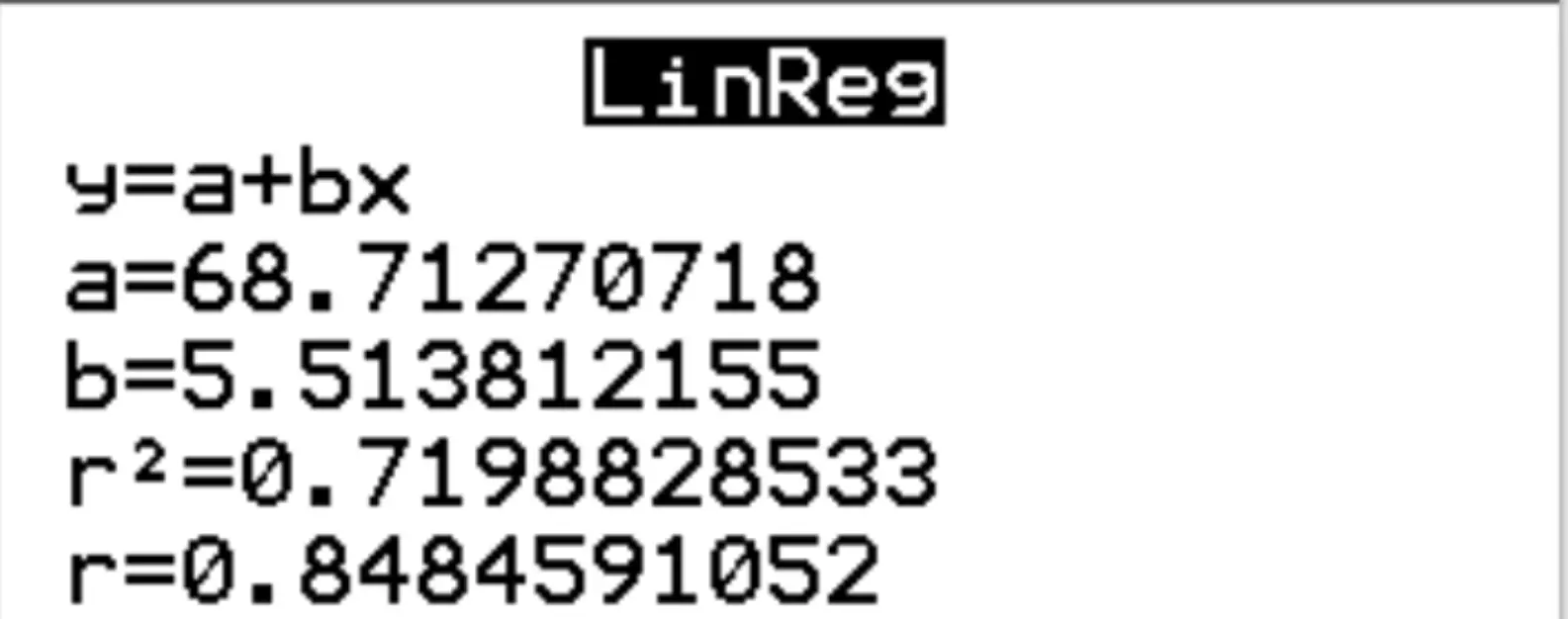
Étape 3 : Interprétez les résultats.
D’après les résultats, nous pouvons voir que l’équation de régression estimée est la suivante :
score à l’examen = 68,7127 + 5,5138*(heures)
Nous interprétons le coefficient des heures comme signifiant que pour chaque heure supplémentaire étudiée, la note à l’examen devrait augmenter de 5,5138 en moyenne. Nous interprétons le coefficient de l’interception comme signifiant que la note attendue à l’examen pour un étudiant qui étudie zéro heure est de 68,7127 .
Nous pouvons utiliser cette équation de régression estimée pour calculer la note attendue à l’examen pour un étudiant, en fonction du nombre d’heures d’études.
Par exemple, un étudiant qui étudie pendant trois heures devrait obtenir une note à l’examen de 85,25 :
score à l’examen = 68,7127 + 5,5138*(3) = 85,25
Nous pouvons également voir que le r au carré pour le modèle de régression est r 2 = 0,7199 .
Cette valeur est connue sous le nom de coefficient de détermination. C’est la proportion de la variance de la variable de réponse qui peut être expliquée par la variable explicative. Dans cet exemple, 71,99 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées.
Ressources additionnelles
Comment créer un tracé résiduel sur une calculatrice TI-84
Comment effectuer une régression quadratique sur une calculatrice TI-84
Comment effectuer une régression exponentielle sur une calculatrice TI-84
Comment effectuer une régression logarithmique sur une calculatrice TI-84
