Comment calculer les valeurs P dans Excel (3 exemples)

En statistiques, nous utilisons des tests d’hypothèse pour déterminer si une affirmation concernant un paramètre de population est vraie ou non.

Lorsque nous effectuons un test d’hypothèse, nous recevons souvent une statistique de test de score T.

Une fois que nous avons trouvé cette statistique du test t-score, nous pouvons alors trouver la valeur p qui lui est associée.

Si cette valeur p est inférieure à une certaine valeur (par exemple 0,10, 0,05, 0,01), alors nous rejetons l’hypothèse nulle du test et concluons que nos résultats sont statistiquement significatifs.

Les exemples suivants montrent comment calculer une valeur p pour une statistique de test dans Excel dans trois scénarios différents.

Exemple 1 : Calculer la valeur P pour un test bilatéral

Supposons qu’un botaniste veuille savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces.

Dans un échantillon aléatoire de 12 plantes, elle constate que la hauteur moyenne de l’échantillon est de 14,33 pouces et que l’écart type de l’échantillon est de 1,37 pouces.

Elle effectue un test d’hypothèse en utilisant les hypothèses nulles et alternatives suivantes :

H ₀ (hypothèse nulle) : μ= 15 pouces

H _A (hypothèse alternative) : μ ≠ 15 pouces

La statistique du test est calculée comme suit :

• t = ( X – µ) / (s/√ n )
• t = (14,33-15) / (1,37/√ 12 )
• t = -1,694

Les degrés de liberté associés à cette statistique de test sont n-1 = 12-1 = 11 .

Pour trouver la valeur p pour cette statistique de test, nous utiliserons la formule suivante dans Excel :

=T.DIST.2T(ABS(-1.694), 11)

La capture d’écran suivante montre comment utiliser cette formule dans la pratique.

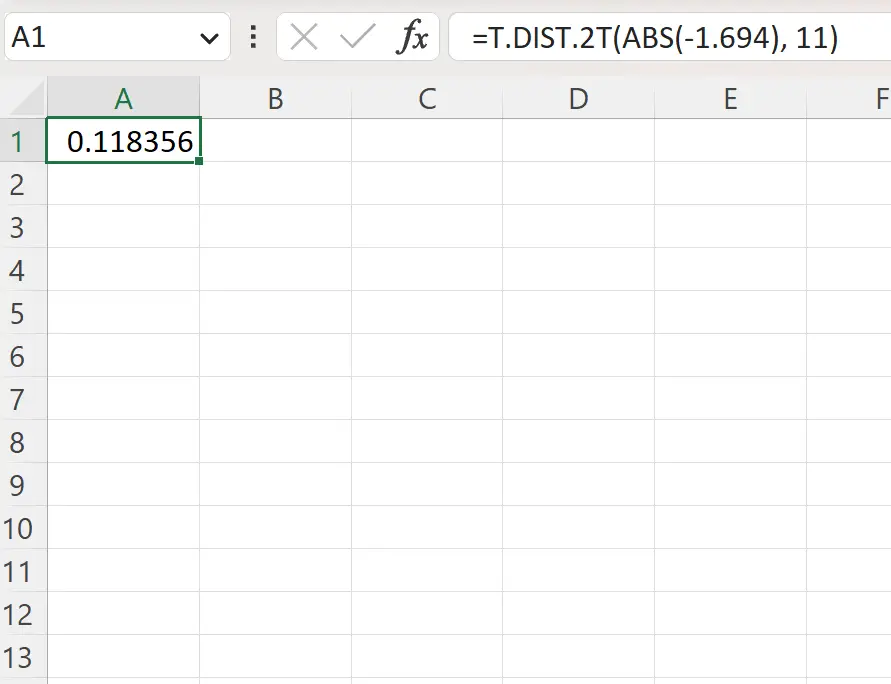
La valeur p bilatérale est de 0,1184 .

Puisque cette valeur n’est pas inférieur à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous n’avons pas suffisamment de preuves pour affirmer que la hauteur moyenne des plantes est différente de 15 pouces.

Exemple 2 : Calculer la valeur P pour le test à gauche

Supposons que l’on suppose que le poids moyen d’un certain gadget produit dans une usine est de 20 grammes. Cependant, un inspecteur estime que le poids moyen réel est inférieur à 20 grammes.

Pour tester cela, il pèse un échantillon aléatoire simple de 20 widgets et obtient les informations suivantes :

• n = 20 widgets
• x = 19,8 grammes
• s = 3,1 grammes

Il effectue ensuite un test d’hypothèse en utilisant les hypothèses nulles et alternatives suivantes :

H ₀ (hypothèse nulle) : μ ≥ 20 grammes

H _A (hypothèse alternative) : μ < 20 grammes

La statistique du test est calculée comme suit :

• t = ( X – µ) / (s/√ n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -.2885

Les degrés de liberté associés à cette statistique de test sont n-1 = 20-1 = 19 .

Pour trouver la valeur p pour cette statistique de test, nous utiliserons la formule suivante dans Excel :

=T.DIST(-.2885, 19, TRUE)

La capture d’écran suivante montre comment utiliser cette formule dans la pratique.

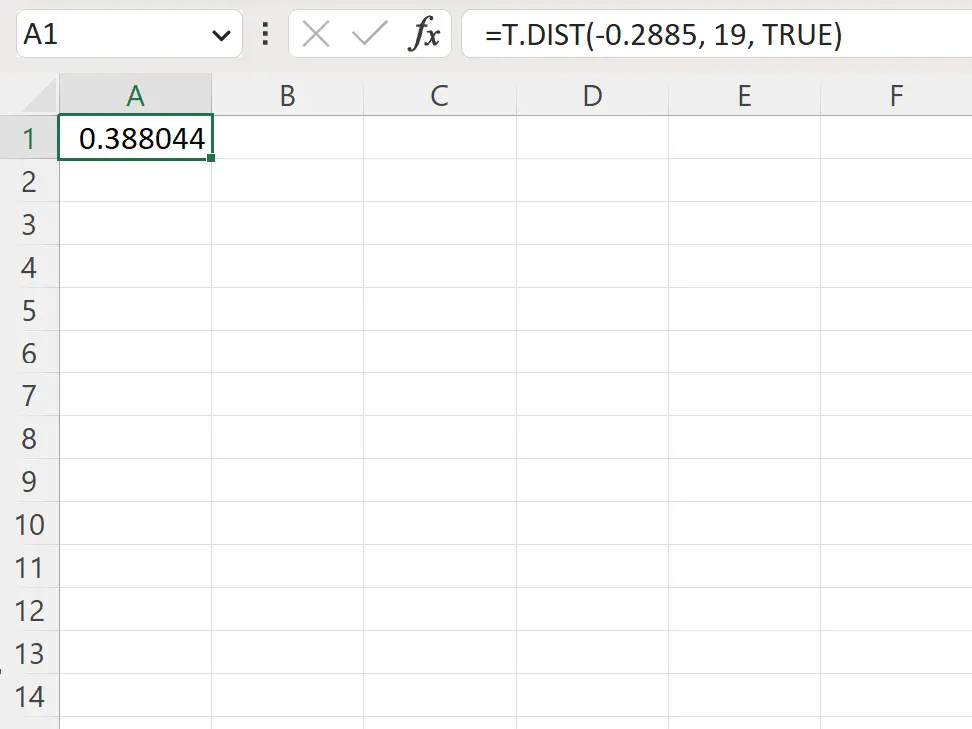
La valeur p à gauche est 0,388044 .

Puisque cette valeur n’est pas inférieur à 0,05, l’inspecteur ne parvient pas à rejeter l’hypothèse nulle. Il ne dispose pas de preuves suffisantes pour affirmer que le poids moyen réel des widgets produits dans cette usine est inférieur à 20 grammes.

Remarque : Nous avons utilisé l’argument TRUE pour spécifier que la fonction de distribution cumulative doit être utilisée lors du calcul de la valeur p.

Exemple 3 : Calculer la valeur P pour le test à queue droite

Supposons que l’on suppose que la hauteur moyenne d’une certaine espèce de plante est de 10 pouces. Cependant, un botaniste affirme que la véritable hauteur moyenne est supérieure à 10 pouces.

Pour tester cette affirmation, elle mesure la hauteur d’un échantillon aléatoire simple de 15 plantes et obtient les informations suivantes :

• n = 15 plantes
• x = 11,4 pouces
• s = 2,5 pouces

Elle effectue ensuite un test d’hypothèse en utilisant les hypothèses nulles et alternatives suivantes :

H ₀ (hypothèse nulle) : μ ≤ 10 pouces

H _A (hypothèse alternative) : μ > 10 pouces

La statistique du test est calculée comme suit :

• t = ( X – µ) / (s/√ n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

Les degrés de liberté associés à cette statistique de test sont n-1 = 15-1 = 14 .

Pour trouver la valeur p pour cette statistique de test, nous utiliserons la formule suivante dans Excel :

=T.DIST.RT(2.1689, 14)

La capture d’écran suivante montre comment utiliser cette formule dans la pratique.

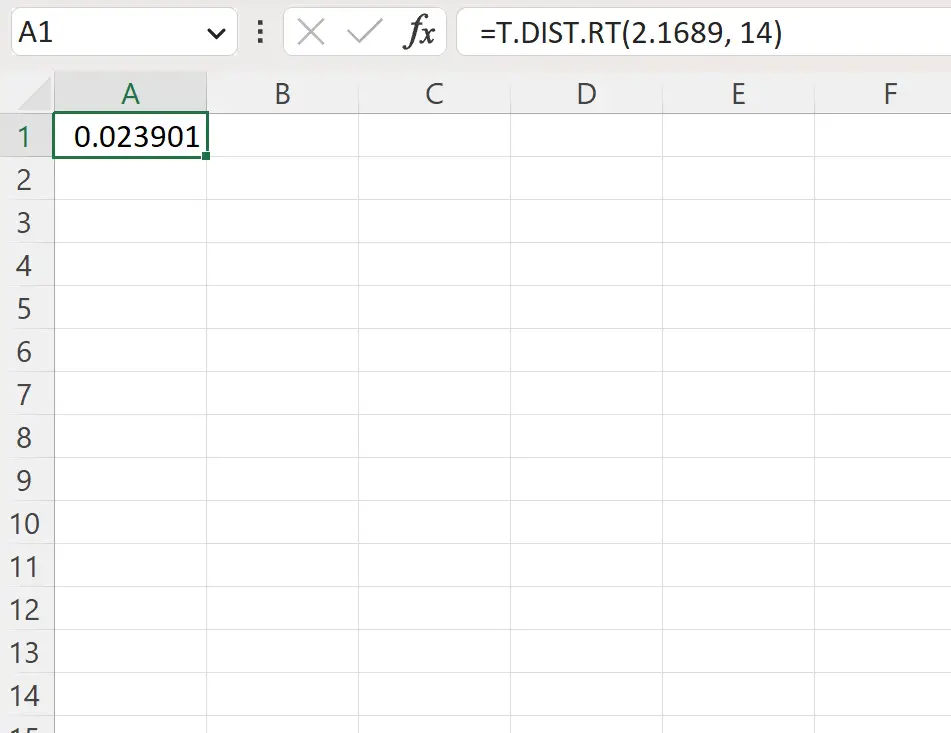
La valeur p à droite est 0,023901 .

Cette valeur étant inférieure à 0,05, le botaniste peut rejeter l’hypothèse nulle. Elle dispose de suffisamment de preuves pour affirmer que la véritable hauteur moyenne de cette espèce de plante est supérieure à 10 pouces.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans Excel :

Comment trouver une valeur P à partir d’un score Z dans Excel
Comment trouver la valeur P d’une statistique F dans Excel
Comment trouver la valeur P d’une statistique du chi carré dans Excel