Comment calculer R-carré à la main
En statistique, R au carré (R 2 ) mesure la proportion de la variance de la variable de réponse qui peut être expliquée par la variable prédictive dans un modèle de régression.
Nous utilisons la formule suivante pour calculer le R au carré :
R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
L’exemple suivant, étape par étape, montre comment calculer manuellement le R au carré pour un modèle de régression donné.
Étape 1 : Créer un ensemble de données
Tout d’abord, créons un ensemble de données :
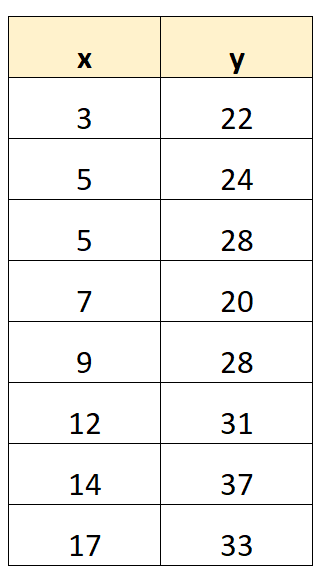
Étape 2 : Calculer les métriques nécessaires
Ensuite, calculons chaque métrique que nous devons utiliser dans la formule R 2 :
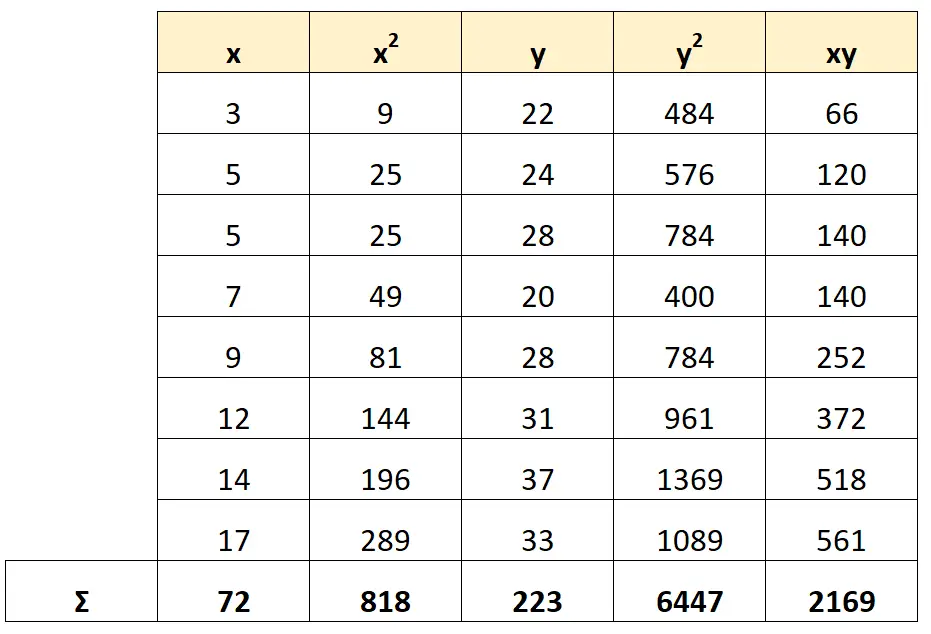
Étape 3 : Calculer le R au carré
Enfin, nous intégrerons chaque métrique dans la formule pour R 2 :
- R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
- R 2 = [ (8*(2169) – (72)(223)) / (√ 8*(818)-(72) 2 * √ 8*(6447)-(223) 2 ) ] 2
- R2 = 0,6686
Remarque : Le n dans la formule représente le nombre d’observations dans l’ensemble de données et s’avère être n = 8 observations dans cet exemple.
En supposant que x est la variable prédictive et y est la variable de réponse dans ce modèle de régression, le R au carré du modèle est de 0,6686 .
Cela nous indique que 66,86 % de la variation de la variable y peut être expliquée par la variable x .
Ressources additionnelles
Introduction à la régression linéaire simple
Introduction à la régression linéaire multiple
R vs R-Carré : quelle est la différence ?
Qu’est-ce qu’une bonne valeur R au carré ?
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus