Moyenne quadratique

Nous expliquons ici ce qu’est la moyenne quadratique et comment elle est calculée. De plus, vous y découvrirez les avantages et les inconvénients de l’utilisation de la moyenne et un exercice résolu étape par étape. Enfin, vous pourrez calculer la moyenne quadratique de n’importe quel ensemble de données avec la calculatrice à la fin de l’article.

Quel est le carré moyen ?

La moyenne quadratique est une mesure de la position centrale des statistiques descriptives. La moyenne quadratique est égale à la racine carrée de la moyenne arithmétique des carrés des données.

La racine carrée moyenne est également appelée racine carrée moyenne , ou RMS .

La formule de la moyenne quadratique est donc la suivante :

La moyenne carrée est particulièrement utile lorsque la variable statistique prend des valeurs positives et négatives, car en mettant chaque donnée au carré, toutes les valeurs deviennent positives. Par conséquent, le carré moyen est utilisé pour analyser les variables dans lesquelles le signe n’est pas important, mais sa valeur absolue.

Par exemple, le carré moyen est utilisé pour étudier les erreurs de mesure, car dans ces cas, nous ne cherchons pas à savoir si l’erreur est positive ou négative, mais plutôt à analyser l’ampleur de l’erreur lors de la mesure.

De plus, les carrés des grands nombres ont des valeurs beaucoup plus élevées que les carrés des petits nombres, donc dans le carré moyen les grands nombres sont plus importants que les petits nombres.

La moyenne carrée est un type de moyenne statistique avec la moyenne arithmétique, la moyenne pondérée, la moyenne géométrique et la moyenne harmonique.

Avantages et inconvénients de la moyenne quadratique

La moyenne quadratique présente des avantages et des inconvénients par rapport aux autres types de moyennes.

Le principal avantage de la moyenne quadratique est qu’elle permet d’obtenir une très bonne approximation de la valeur moyenne d’une variable discrète. En revanche, le grand inconvénient de la moyenne carrée est que son calcul est assez compliqué, puisqu’il faut effectuer plusieurs opérations.

En revanche, la moyenne quadratique est très utile pour analyser les mesures d’erreur. Elle donne également beaucoup plus d’importance aux valeurs élevées, même si cette propriété implique qu’une mauvaise mesure altèrera considérablement le résultat de la valeur efficace.

Comment calculer la moyenne quadratique

Pour calculer la moyenne quadratique, les étapes suivantes doivent être effectuées :

1. Calculez le carré de chaque donnée statistique.
2. Additionnez tous les carrés calculés à l’étape précédente.
3. Divisez le résultat par le nombre de données dans l’échantillon.
4. Trouvez la racine carrée de la valeur précédente.
5. Le résultat obtenu est la moyenne carrée de l’échantillon statistique.

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la moyenne quadratique de n’importe quel ensemble de données.

Exemple du carré moyen

Une fois que nous savons comment obtenir la moyenne quadratique, nous allons déterminer la moyenne quadratique d’un ensemble de données à titre d’exemple.

• Dans un cours de laboratoire universitaire, le professeur demande à ses étudiants de faire une expérience avec des produits chimiques. L’objectif de l’expérience chimique est d’obtenir une solution de 3 litres au total. Les groupes d’étudiants ont obtenu les données suivantes :

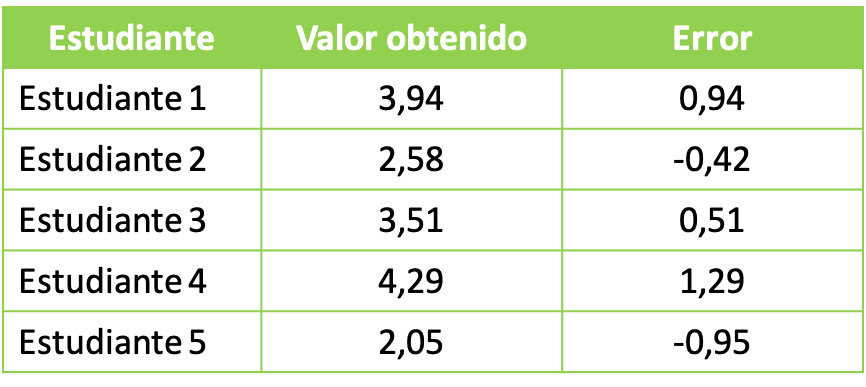
Afin d’étudier les données statistiques obtenues, nous procédons au calcul de la valeur de la moyenne carrée avec l’erreur obtenue par chaque groupe. Nous appliquons donc la formule de la moyenne quadratique :

Et nous substituons les données dans la formule et calculons la moyenne quadratique :

Ainsi, l’erreur moyenne obtenue dans l’expérience, selon la moyenne quadratique, est de 0,88 litre.

Calculateur du carré moyen

Entrez les données de n’importe quel échantillon statistique dans la calculatrice suivante pour calculer sa moyenne quadratique. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.