Comment trouver le centre et la propagation d’un tracé de points

Un tracé de points est un type de tracé qui affiche les fréquences des valeurs dans un ensemble de données à l’aide de points empilés.

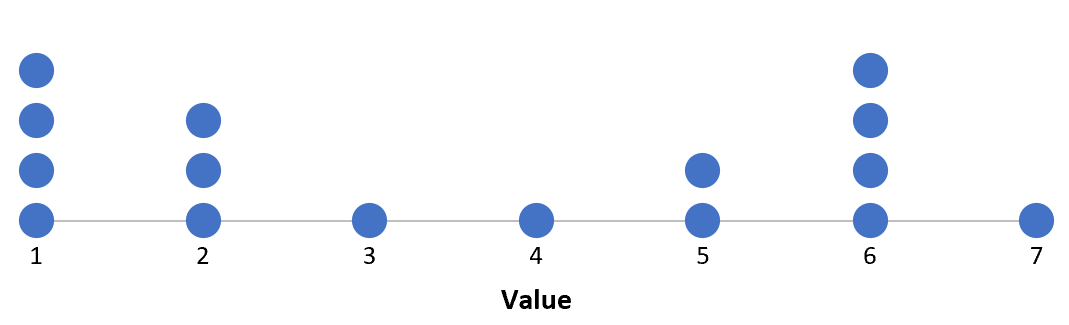
Souvent, lorsque nous créons un diagramme de points, nous souhaitons quantifier le centre et la répartition :

• Centre : Le point central de l’ensemble de données. Nous utilisons souvent la médiane pour mesurer cela.
• Spread : la répartition des valeurs dans l’ensemble de données. Nous utilisons souvent la plage pour mesurer cela.

En connaissant uniquement ces deux valeurs, nous pouvons avoir une bonne idée de la façon dont les valeurs sont distribuées dans un ensemble de données donné.

Les exemples suivants montrent comment trouver le centre et l’étendue d’un tracé de points dans la pratique.

Exemple 1 : Diagramme de points des fautes commises

Le diagramme de points suivant montre le nombre de fautes commises dans un certain match par des joueurs de basket-ball :

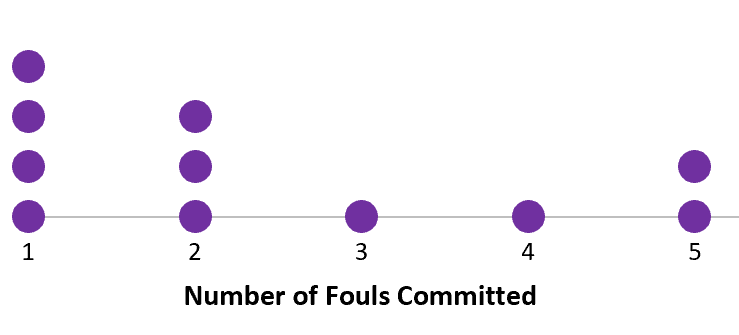
Voici comment trouver le centre et la répartition des valeurs dans cet ensemble de données :

Centre : Nous pouvons utiliser la médiane pour mesurer le « centre » de l’ensemble de données. La médiane représente la valeur médiane de l’ensemble de données. Pour trouver la médiane pour cet ensemble de données particulier, nous pouvons répertorier chaque valeur et identifier la valeur médiane :

Valeurs des données : 1, 1, 1, 1, 2, 2 , 2, 3, 4, 5, 5

La valeur médiane dans cet ensemble de données est 2 .

Spread : Nous pouvons utiliser la plage pour mesurer la « propagation » des valeurs dans l’ensemble de données. La plage représente la différence entre la valeur la plus grande et la plus petite.

Dans cet ensemble de données, nous pouvons voir que la plus grande valeur est 5 et la plus petite valeur est 1, la plage peut donc être calculée comme suit : 5 – 1 = 4 .

Exemple 2 : diagramme de points des résultats des tests

Le diagramme de points suivant montre les résultats des tests des élèves d’une classe particulière :

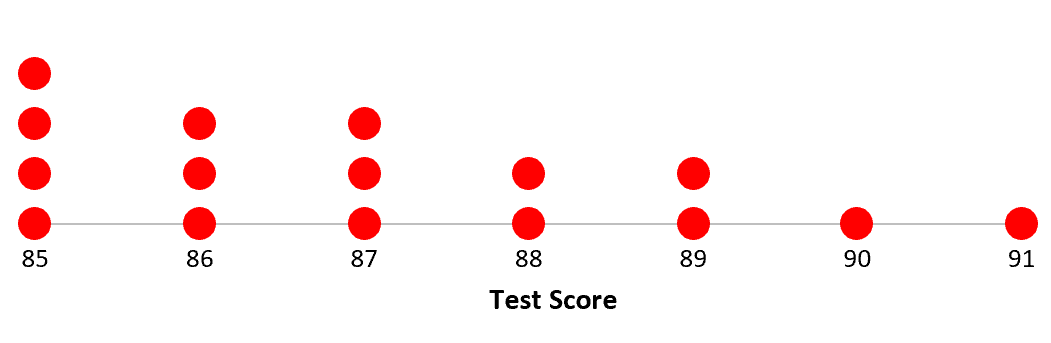
Voici comment trouver le centre et la répartition des valeurs dans cet ensemble de données :

Centre : Nous pouvons utiliser la médiane pour mesurer le « centre » de l’ensemble de données. Pour trouver la médiane pour cet ensemble de données particulier, nous pouvons répertorier chaque valeur et identifier la valeur médiane :

Valeurs des données : 85, 85, 85, 85, 86, 86, 86 , 87 , 87, 87, 88, 88, 89, 89, 90, 91

Cet ensemble de données comporte un nombre pair de valeurs, la médiane sera donc la moyenne des deux valeurs du milieu. La médiane s’avère être de 87 .

Spread : Nous pouvons utiliser la plage pour mesurer la « propagation » des valeurs dans l’ensemble de données, qui représente la différence entre la plus grande et la plus petite valeur.

Dans cet ensemble de données, nous pouvons voir que la plus grande valeur est 91 et la plus petite est 85, la plage peut donc être calculée comme suit : 91 – 85 = 6 .

Ressources additionnelles

Les didacticiels suivants expliquent comment créer des tracés de points dans différents logiciels statistiques :

Comment créer un tracé de points dans Excel
Comment créer un tracé de points dans R