Centile, quartile et quantile : quelle est la différence ?

Trois termes que les élèves confondent souvent dans les statistiques sont les centiles, les quartiles et les quantiles.

Voici une définition simple de chacun :

Percentiles : plage de 0 à 100.

Quartiles : intervalle de 0 à 4.

Quantiles : vont de n’importe quelle valeur à n’importe quelle autre valeur.

Notez que les centiles et les quartiles sont simplement des types de quantiles.

Certains types de quantiles ont même des noms spécifiques, notamment :

• Les 4 quantiles sont appelés quartiles .
• Les 5 quantiles sont appelés quintiles .
• Les 8 quantiles sont appelés octiles .
• Les 10 quantiles sont appelés déciles .
• Les 100 quantiles sont appelés centiles .

Notez que les percentiles et les quartiles partagent la relation suivante :

• 0 centile = 0 quartile (également appelé minimum)
• 25e centile = 1er quartile
• 50e centile = 2e quartile (également appelé médiane)
• 75e centile = 3e quartile
• 100e centile = 4e quartile (également appelé maximum)

Exemple : Rechercher des centiles et des quartiles

Supposons que nous ayons l’ensemble de données suivant avec 20 valeurs :

À l’aide de logiciels statistiques (comme Excel, R, Python, etc.), nous pouvons trouver les centiles et quartiles suivants pour cet ensemble de données :

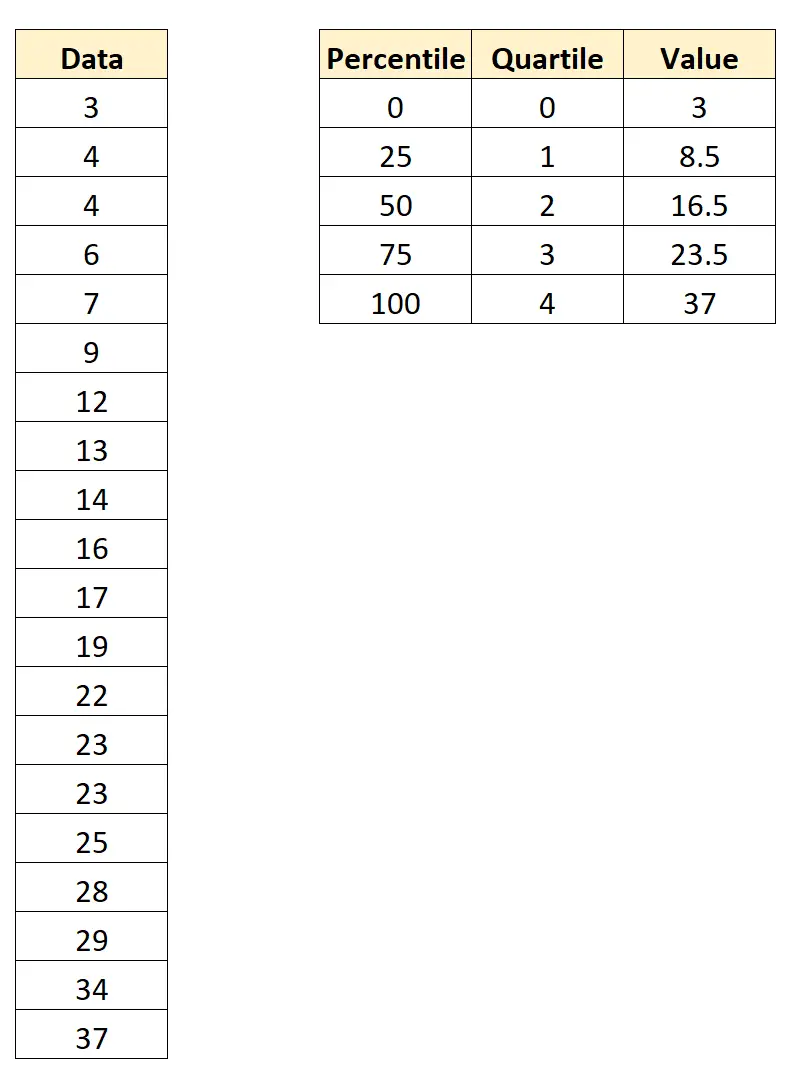
Voici comment interpréter ces valeurs :

• Le centile 0 et le quartile 0 sont 3 .
• Le 25e centile et 1er quartile est de 8,5 .
• Le 50e centile et 2e quartile est de 16,5 .
• Le 75e centile et 3e quartile est de 23,5 .
• Le 100e centile et le 4e quartile sont 37 .

Quand utiliser les centiles par rapport aux quartiles

Les percentiles peuvent être utilisés pour répondre à des questions telles que :

Quel score un étudiant doit-il obtenir à un test particulier pour figurer dans les 10 % des meilleurs scores ?

Pour répondre à cette question, nous trouverions le 90e percentile de tous les scores, qui est la valeur qui sépare les 90 % des valeurs inférieures des 10 % supérieures.

Quelles hauteurs englobent les 40 % des hauteurs moyennes des élèves d’une école particulière ?

Pour répondre à cette question, nous trouverions le 70e percentile des hauteurs et le 30e percentile des hauteurs, qui sont les deux valeurs qui déterminent les limites supérieure et inférieure pour les 40 % moyens des hauteurs.

Les quartiles peuvent être utilisés pour répondre à des questions telles que :

Quel score un élève doit-il obtenir à un test pour figurer dans le quart supérieur des scores ?

Pour répondre à cette question, nous trouverions le 3e quartile de tous les scores, qui est la valeur qui sépare les 75 % des valeurs inférieures des 25 % supérieures.

Quelle est l’étendue interquartile d’un ensemble de données donné ?

L’intervalle interquartile (IQR) est l’intervalle des 50 % moyens des valeurs des données. Pour trouver l’IQR pour un ensemble de données donné, nous pouvons calculer le 3ème quartile – le 1er quartile.

Ressources additionnelles

Comment calculer les centiles en R
Comment calculer les quartiles dans R
Comment calculer l’intervalle interquartile dans Excel
Comment calculer l’intervalle interquartile sur une calculatrice TI-84