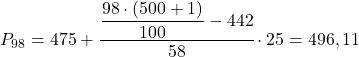Percentiles (statistiques)

Cet article explique ce qu’est un centile et comment il est calculé. Vous trouverez des exercices de percentiles résolus et, en outre, vous pourrez calculer n’importe quel percentile de votre échantillon de données avec un calculateur en ligne.

Que sont les centiles ?

En statistiques, les centiles sont les valeurs qui divisent un ensemble de données ordonnées en cent parties égales. Ainsi, un percentile indique la valeur en dessous de laquelle se situe un pourcentage de l’ensemble de données.

Par exemple, la valeur du 35e centile est supérieure à 35 % des données observées, mais inférieure au reste des données.

Les centiles sont représentés par la lettre majuscule P et l’indice du centile, c’est-à-dire que le 1er centile est P ₁ , le 40e centile est P ₄₀ , le 79e centile est P ₇₉ , et ainsi de suite.

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer les percentiles de n’importe quel ensemble de données.

De même, les centiles sont une mesure de la position non centrale avec les quartiles, les quintiles et les déciles. Vous pouvez vérifier la signification de chacun de ces types de quantiles sur notre site Web.

Il convient de noter que le terme percentiles est également utilisé pour comparer le poids et la taille d’un bébé avec les valeurs standard d’autres bébés, car il existe des tables de croissance avec des valeurs enregistrées qui permettent de déterminer si le bébé grandit correctement ou non. . .

Comment calculer les centiles

Pour calculer la position d’un centile d’une série de données statistiques, vous devez multiplier le nombre de centile par la somme du nombre total de points de données plus un et diviser le résultat par cent.

La formule du percentile est donc :

Attention : cette formule nous indique la position du centile, mais pas sa valeur. Le percentile sera la donnée située à la position obtenue par la formule.

Cependant, parfois le résultat de cette formule nous donnera un nombre décimal, il faut donc distinguer deux cas selon que le résultat est un nombre décimal ou non :

• Si le résultat de la formule est un nombre sans partie décimale , le centile correspond aux données qui se trouvent dans la position fournie par la formule ci-dessus.
• Si le résultat de la formule est un nombre avec une partie décimale , la valeur exacte du percentile est calculée à l’aide de la formule suivante :

Où x _i et x _i+1 sont les nombres des positions entre lesquelles se trouve le nombre obtenu par la première formule, et d est la partie décimale du nombre obtenu par la première formule.

Vous pensez peut-être maintenant qu’il est compliqué de trouver les percentiles d’un échantillon statistique ou d’une population car la méthode comporte de nombreuses étapes, mais c’est en réalité facile. Lisez les deux exemples concrets suivants et je suis sûr que vous le comprendrez beaucoup mieux.

Remarque : la communauté scientifique n’est pas encore totalement d’accord sur le calcul des centiles, vous trouverez donc peut-être un livre de statistiques qui l’explique un peu différemment.

Exemples de calcul de percentile

Comme vous l’avez vu ci-dessus dans l’explication de la façon de trouver les centiles d’un échantillon, le calcul varie selon que le résultat de la première formule est décimal ou non. C’est pourquoi vous trouverez ci-dessous deux exemples résolus, un pour chaque cas.

Exemple 1

• À partir des données présentées dans le tableau suivant, calculez les 1er, 43e et 89e centiles.

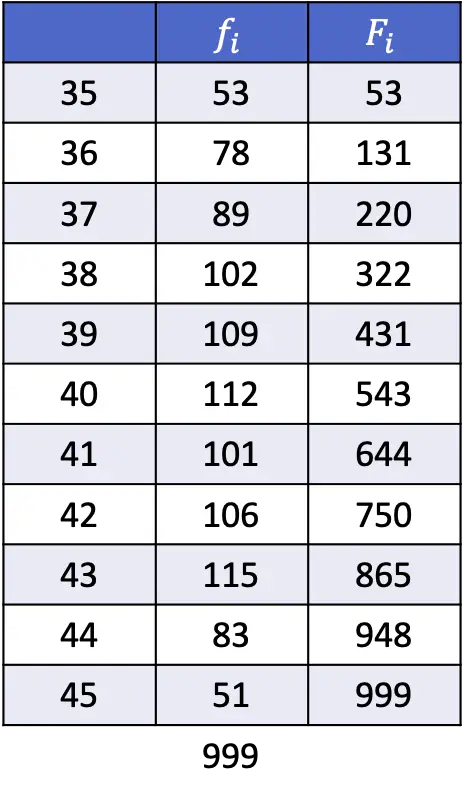
Comme expliqué dans la section précédente, la formule qui permet de trouver la position d’un percentile est :

Dans ce cas, la taille de l’échantillon pour cet exercice est de 999 données statistiques, donc pour calculer la position du premier centile, nous devons substituer 999 à n et 1 à k :

Ainsi le 1er centile sera celui dont la fréquence absolue cumulée est immédiatement supérieure à 10, qui dans ce cas est 35 puisqu’elle a une fréquence absolue cumulée de 53.

Pour déterminer le 43ème percentile il faut utiliser la même formule mais, évidemment, cette fois on remplace le k par 43.

La fréquence cumulée absolue immédiatement au-dessus de 430 est 431 des données 39, donc le 43e percentile est égal à 39.

Finalement, on applique la même formule pour obtenir le 89ème percentile :

La fréquence absolue cumulée de la valeur 44 est de 948, ce qui est immédiatement supérieur à 890. Par conséquent, le 89e percentile est de 44.

Exemple 2

• Trouvez les 35e et 67e centiles de la série de données suivante :

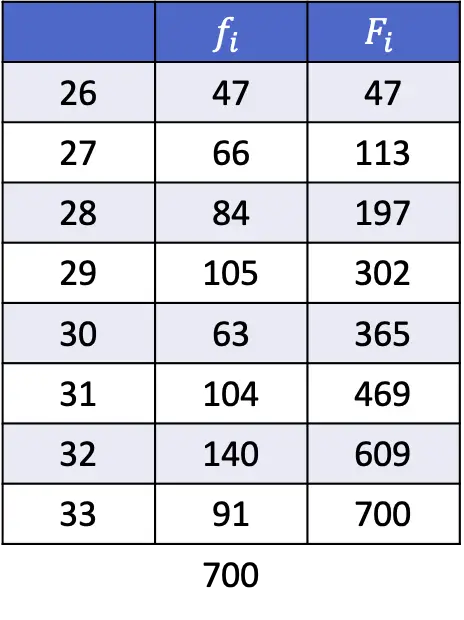
Même si dans cet exercice nous devrons faire plus de calculs, le principe est toujours le même : il faut calculer la position du percentile avec l’expression suivante.

Ainsi, pour calculer le 35ème percentile on remplace le k par 35 et le n par le nombre total de données, soit 700 :

Mais cette fois, nous avons obtenu un nombre décimal à partir de la formule, nous devons donc appliquer l’expression algébrique suivante pour calculer la valeur centile exacte :

Le nombre donné par la première formule est 245,35, donc le 35ème centile se situe entre les positions 245 et 246, qui correspondent respectivement aux valeurs 29 et 29. Par conséquent, x _i vaut 29, x _i+1 vaut 29 et d vaut la partie décimale du nombre obtenu, soit 0,35.

Pour trouver le 67e centile, nous devons utiliser la même méthode. Nous calculons d’abord la position centile :

Le nombre obtenu 469,67 indique que le centile sera entre les positions 469 et 470, dont les valeurs sont 31 et 32. Par conséquent, nous utilisons la deuxième formule dans le processus pour trouver la valeur exacte du centile :

calculateur de centile

Entrez un ensemble de données statistiques et le nombre centile que vous souhaitez calculer dans la calculatrice suivante. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Percentiles dans les données groupées

Pour calculer les centiles lorsque les données sont regroupées dans des groupes , nous devons d’abord trouver le groupe ou la classe dans laquelle se situe le centile à l’aide de la formule suivante :

Le centile sera donc dans l’intervalle dont la fréquence absolue est immédiatement supérieure au nombre obtenu dans l’expression précédente.

Et une fois que l’on connaît déjà l’intervalle auquel appartient le percentile, il faut appliquer la formule suivante pour trouver la valeur exacte du percentile :

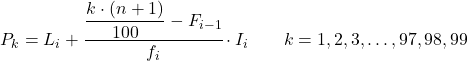
Où:

• L _i est la limite inférieure de l’intervalle dans lequel se trouve le centile.
• n est le nombre total d’observations.
• F _i-1 est la fréquence absolue cumulée de l’intervalle précédent.
• f _i est la fréquence absolue de l’intervalle dans lequel se situe le centile.
• I _i est la largeur de l’intervalle centile.

Vous trouverez ci-dessous un exercice étape par étape expliquant comment obtenir les centiles lorsque les données sont exprimées en intervalles. Plus précisément, les 29e, 52e et 98e percentiles sont calculés.

Les données de cet échantillon sont regroupées sous forme d’intervalles, nous devons donc effectuer deux étapes pour déterminer les centiles : nous devons d’abord trouver l’intervalle dans lequel se situe le centile, puis appliquer la formule pour calculer la valeur exacte du centile.

Ainsi, on retrouve la position du 29ème centile avec l’expression suivante :

L’intervalle percentile sera celui dont la fréquence absolue cumulée est immédiatement supérieure à 145,29, qui dans ce cas est l’intervalle [350,375) dont la fréquence absolue cumulée est 175. Et une fois que l’on connaît l’intervalle percentile, on applique la formule suivante pour calculer son valeur exacte:

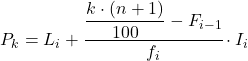
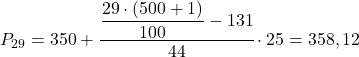
Maintenant, nous répétons la même procédure pour calculer le 52e percentile. Nous calculons d’abord son intervalle :

L’intervalle du 52e percentile est [400,425) puisque sa fréquence absolue cumulée (298) est celle immédiatement supérieure à 260,52. La valeur exacte du centile sera donc :

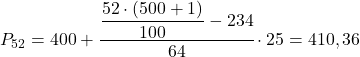
Enfin, nous allons trouver le 98ème centile. Comme toujours, nous calculons d’abord l’intervalle où il se trouve :

Et une fois que nous connaissons l’intervalle où se trouve le centile, nous calculons sa valeur exacte avec la formule suivante :