Comment effectuer un test d’indépendance du chi carré dans Stata

Un test d’indépendance du chi carré est utilisé pour déterminer s’il existe ou non une association significative entre deux variables catégorielles.

Ce didacticiel explique comment effectuer un test d’indépendance du chi carré dans Stata.

Exemple : test du chi carré d’indépendance dans Stata

Pour cet exemple, nous utiliserons un ensemble de données appelé auto , qui contient des informations sur 74 automobiles différentes de 1978.

Suivez les étapes suivantes pour effectuer un test d’indépendance du chi carré afin de déterminer s’il existe une association significative entre les deux variables suivantes :

• rep78 : le nombre de fois où la voiture a été réparée en 1978 (varie de 1 à 5)
• étranger : si le type de voiture est étranger ou non (0 = non, 1 = oui)

Étape 1 : Chargez et affichez les données brutes.

Tout d’abord, nous allons charger les données en tapant la commande suivante :

utilisation automatique du système

Nous pouvons visualiser les données brutes en tapant la commande suivante :

br

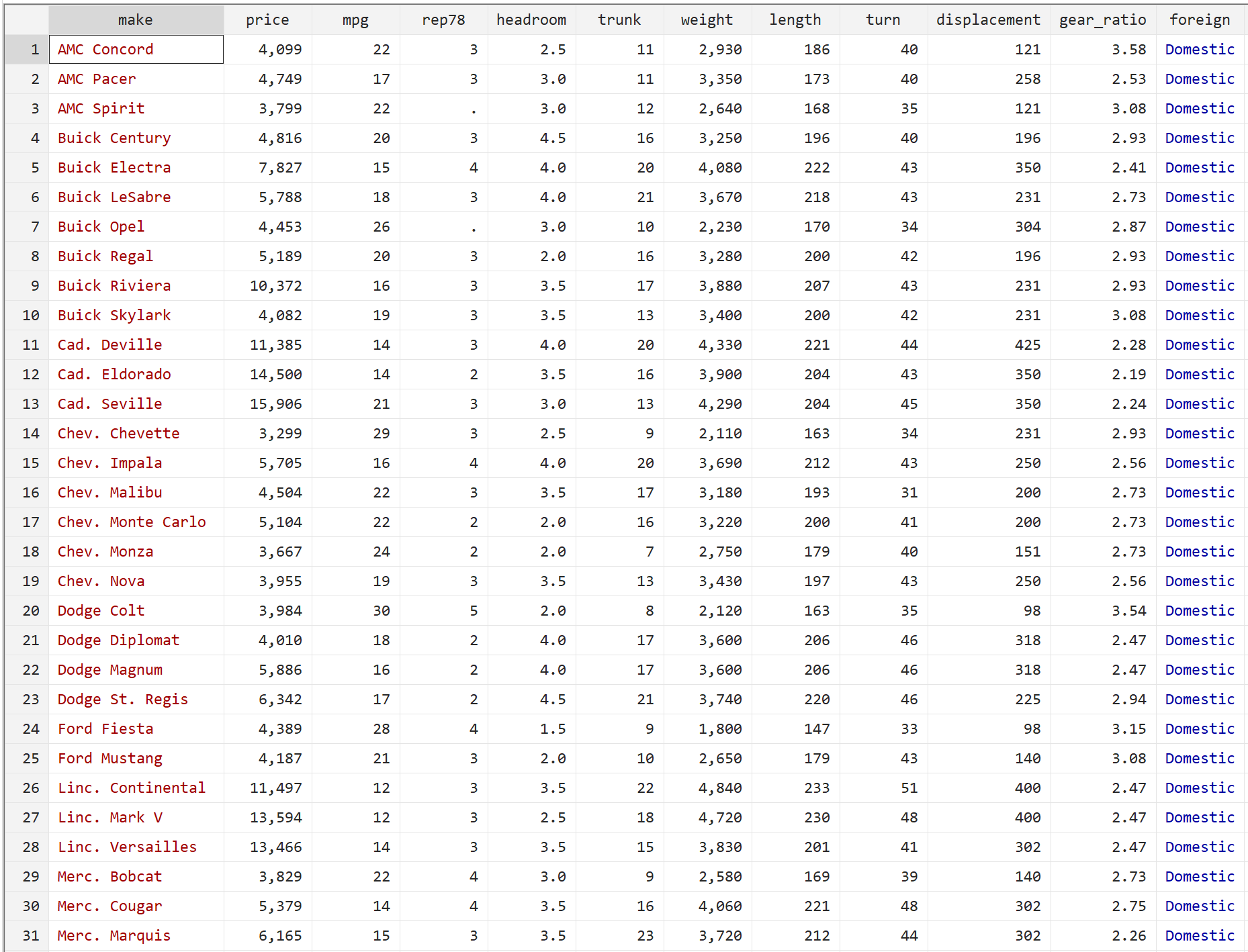
Chaque ligne affiche des informations sur une voiture individuelle, notamment le prix, le mpg, le poids, la longueur et diverses autres variables. Les deux seules variables qui nous intéressent sont rep78 et Foreign .

Étape 3 : Effectuez le test d’indépendance du chi carré.

Nous utiliserons la syntaxe suivante pour effectuer le test :

onglet première_variable seconde_variable, chi2

Voici la syntaxe exacte que nous utiliserons dans notre cas :

onglet rep78 étranger, chi2

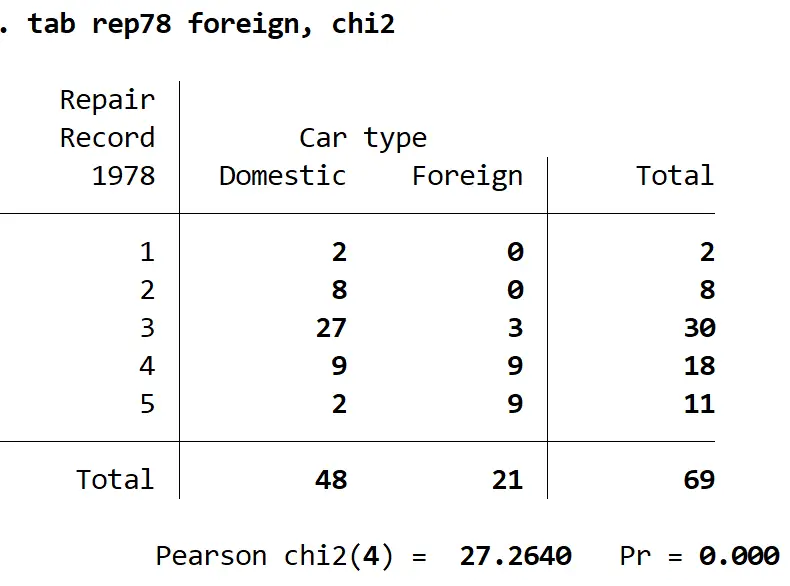
Voici comment interpréter le résultat :

Tableau récapitulatif : Ce tableau montre le nombre total de chaque combinaison de rep78 et étranger . Par exemple

• Il y avait 2 voitures domestiques et 1 réparation en 1978.
• Il y avait 8 voitures domestiques et ont reçu 2 réparations en 1978.
• Il y avait 27 voitures domestiques qui ont reçu 3 réparations en 1978.

Et ainsi de suite.

Pearson chisq(4) : il s’agit de la statistique du test du chi carré pour le test. Il s’avère que c’est 27,2640.

Pr : Il s’agit de la valeur p associée à la statistique du test du Chi carré. Il s’avère que c’est 0,000. Comme cette valeur est inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle selon laquelle les deux variables sont indépendantes. Nous disposons de suffisamment de preuves pour conclure qu’il existe une association statistiquement significative entre le fait qu’une voiture soit étrangère ou non et le nombre total de réparations qu’elle a subies.