Comment effectuer un test Chow dans R
Un test de Chow est utilisé pour tester si les coefficients de deux modèles de régression différents sur des ensembles de données différents sont égaux.
Ce test est généralement utilisé dans le domaine de l’économétrie avec des données de séries chronologiques pour déterminer s’il existe une rupture structurelle dans les données à un moment donné.
Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer un test Chow dans R.
Étape 1 : Créer les données
Tout d’abord, nous allons créer de fausses données :
#create data data <- data.frame(x = c(1, 1, 2, 3, 4, 4, 5, 5, 6, 7, 7, 8, 8, 9, 10, 10, 11, 12, 12, 13, 14, 15, 15, 16, 17, 18, 18, 19, 20, 20), y = c(3, 5, 6, 10, 13, 15, 17, 14, 20, 23, 25, 27, 30, 30, 31, 33, 32, 32, 30, 32, 34, 34, 37, 35, 34, 36, 34, 37, 38, 36)) #view first six rows of data head(data) x y 1 1 3 2 1 5 3 2 6 4 3 10 5 4 13 6 4 15
Étape 2 : Visualisez les données
Ensuite, nous allons créer un nuage de points simple pour visualiser les données :
#load ggplot2 visualization package library(ggplot2) #create scatterplot ggplot(data, aes(x = x, y = y)) + geom_point(col='steelblue', size=3)
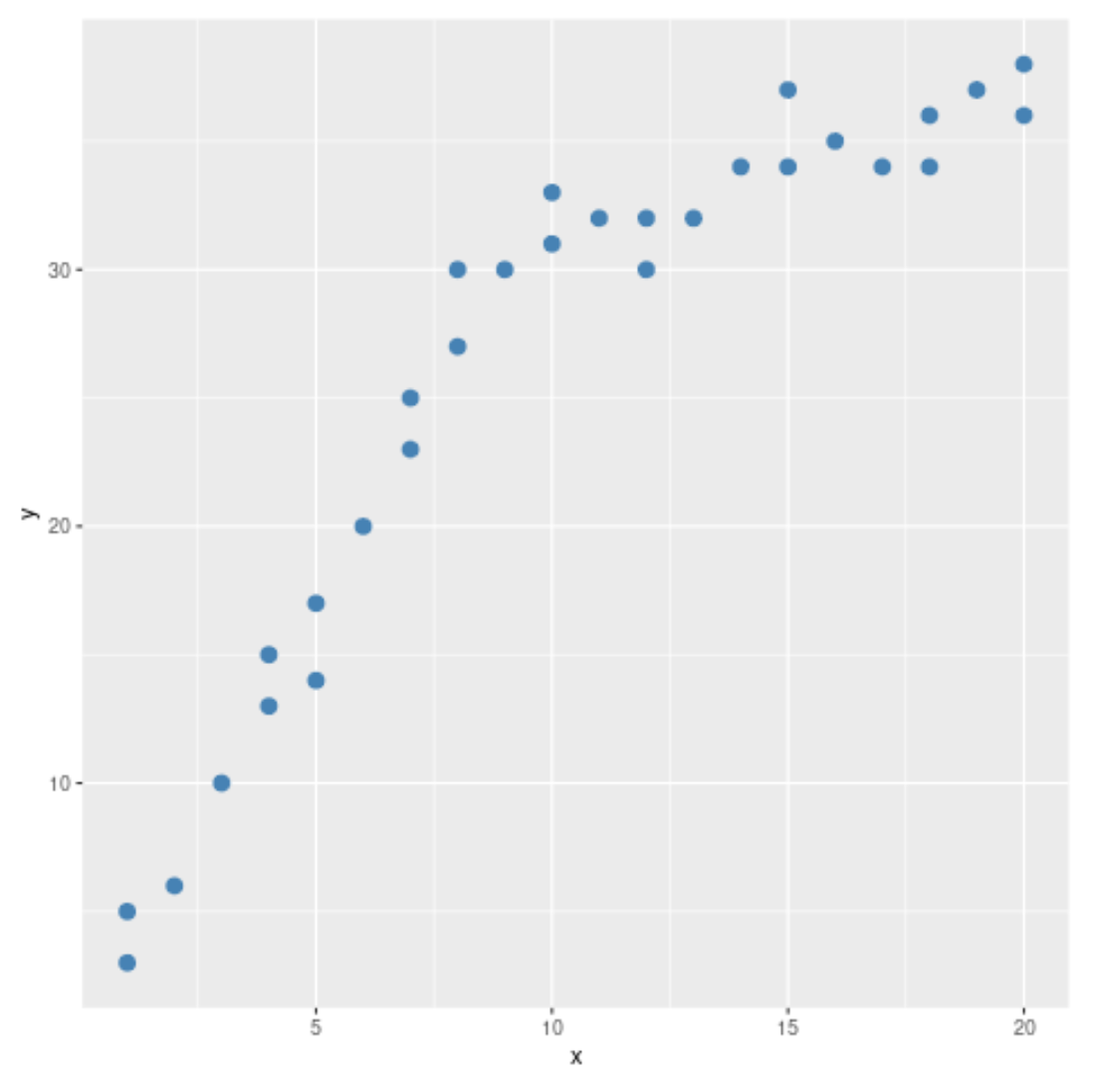
À partir du nuage de points, nous pouvons voir que le modèle dans les données semble changer à x = 10. Ainsi, nous pouvons effectuer le test de Chow pour déterminer s’il existe un point de rupture structurelle dans les données à x = 10.
Étape 3 : Effectuer le test Chow
Nous pouvons utiliser la fonction sctest du package strucchange pour effectuer un test Chow :
#load strucchange package library(strucchange) #perform Chow test sctest(data$y ~ data$x, type = "Chow", point = 10) Chow test data: data$y ~ data$x F = 110.14, p-value = 2.023e-13
À partir du résultat du test, nous pouvons voir :
- Statistique du test F : 110,14
- Valeur p : <.0000
Puisque la valeur p est inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle du test. Cela signifie que nous disposons de suffisamment de preuves pour affirmer qu’un point de rupture structurelle est présent dans les données.
En d’autres termes, deux droites de régression peuvent adapter le modèle dans les données plus efficacement qu’une seule droite de régression.
