什么是分类分布？

分类分布是一种离散概率分布，描述随机变量取属于K个类别之一的值的概率，其中每个类别都与一个概率相关联。

对于要分类为分类分布的分布，它必须满足以下条件：

• 这些类别是离散的。
• 有两个或多个潜在类别。
• 随机变量在每个类别中取值的概率必须在 0 到 1 之间。
• 所有类别的概率总和必须为 1。

分类分布最明显的例子是与掷骰子相关的结果的分布。有K = 6 种潜在结果，每种结果的概率为 1/6：

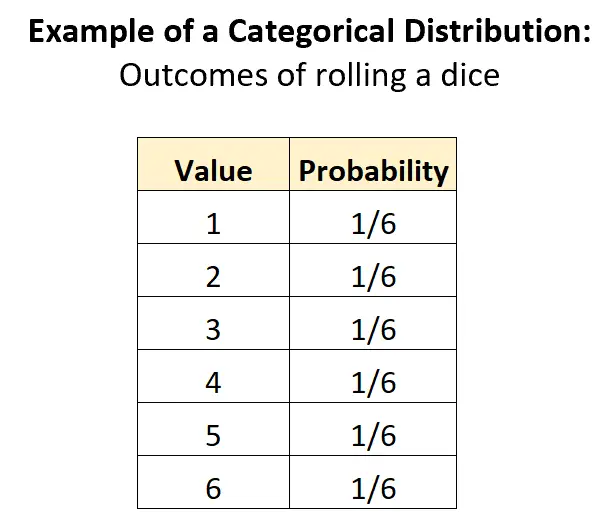
该分布满足分类分布的所有标准：

• 类别是离散的（例如随机变量只能取离散值 – 1, 2, 3, 4, 5, 6）
• 有两个或多个潜在类别。
• 每个类别的概率都在 0 到 1 之间。
• 概率之和为 1：1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1。

一般规则：

如果您可以计算结果的数量，那么您正在使用离散随机变量 – 例如，计算硬币正面朝上的次数。

但如果您可以测量结果，那么您正在使用连续随机变量 – 例如测量身高、体重、时间等。

分类分布的其他示例

现实世界中有许多分类分布，包括：

例1：抛硬币。

当我们抛硬币时，有 2 个潜在的离散结果，每个结果的概率在 0 到 1 之间，概率之和等于 1：

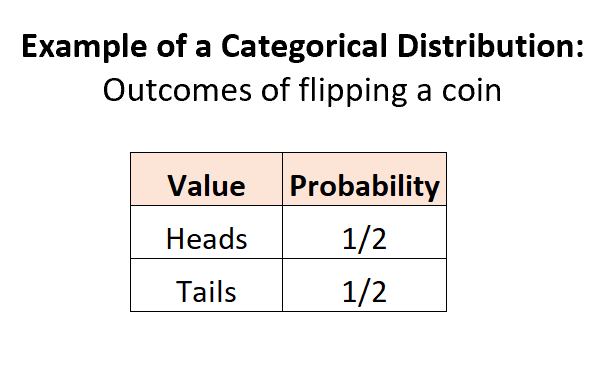
示例 2：选择瓮中的弹珠。

假设一个瓮中有 5 个红色弹珠、3 个绿色弹珠和 2 个紫色弹珠。如果我们从瓮中随机选择一个球，则有 3 个潜在的离散结果，每个结果的概率在 0 到 1 之间，概率之和等于 1：

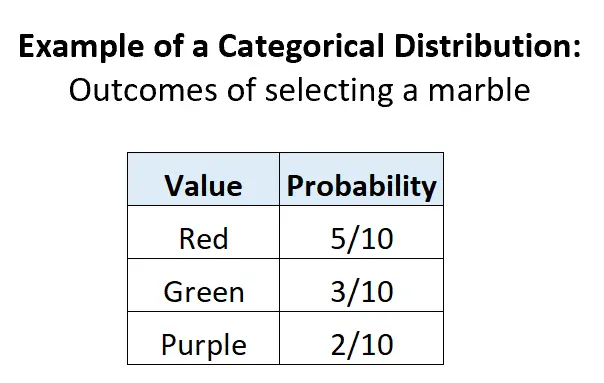
示例 3：从一副牌中选择一张牌。

如果我们从标准的 52 张牌中随机选择一张牌，则有 13 种潜在的离散结果，每种结果的概率在 0 到 1 之间，概率之和等于 1：

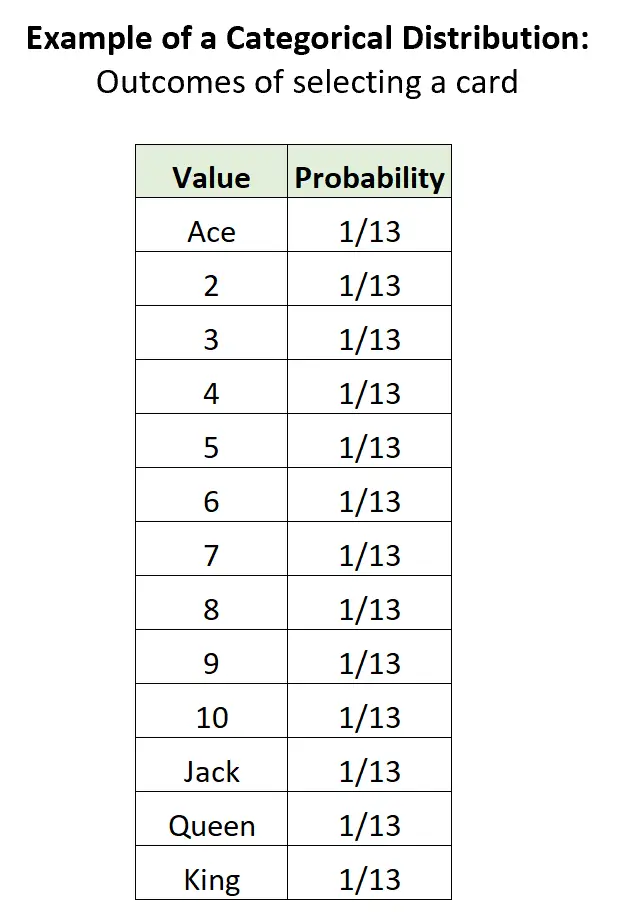
与其他发行版的关系

对于要分类为分类分布的分布，它必须具有K ≥ 2 个潜在结果并且n = 1 次试验。

使用此术语，分类分布类似于以下分布：

伯努利分布： K = 2 个结果， n = 1 个测试

二项式分布： K = 2 个终点，n ≥ 1 项试验

多项分布： K ≥ 2 个结果，n ≥ 试验

其他资源

什么是随机变量？
二项分布简介
多项式分布简介