指数分布简介

指数分布是一种概率分布，用于对我们必须等待特定事件发生的时间进行建模。

该分布可用于回答以下问题：

• 零售商应该等待顾客进入商店多久？
• 笔记本电脑在损坏之前还能继续工作多长时间？
• 汽车电池在耗尽之前还能继续工作多长时间？
• 某个地区下一次火山喷发要等多久？

在每种情况下，我们想要计算需要等待多长时间才能发生特定事件。因此，每个场景都可以使用指数分布进行建模。

指数分布：PDF 和 CDF

如果随机变量X服从指数分布，则X的概率密度函数可以写为：

f (x; λ) = λe ^{– λx}

金子：

• λ：速率参数（计算公式为 λ = 1/μ）
• e：约等于 2.718 的常数

累积分布函数

F (x; λ) = 1 – e ^-λx

在实践中，CDF 最常用于计算与指数分布相关的概率。

例如，假设某个间歇泉喷发之间的平均分钟数为 40 分钟。我们等待不到 50 分钟就会爆发的可能性有多大？

为了解决这个问题，我们首先需要计算速率参数：

• λ = 1/μ
• λ = 1/40
• λ = 0.025

我们可以将 λ = 0.025 和 x = 50 代入 CDF 公式：

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0.025(50)
• P(X≤50)=0.7135

我们需要等待不到 50 分钟才能看到下一次喷发的概率是0.7135 。

可视化指数分布

下图显示了随机变量的概率密度函数

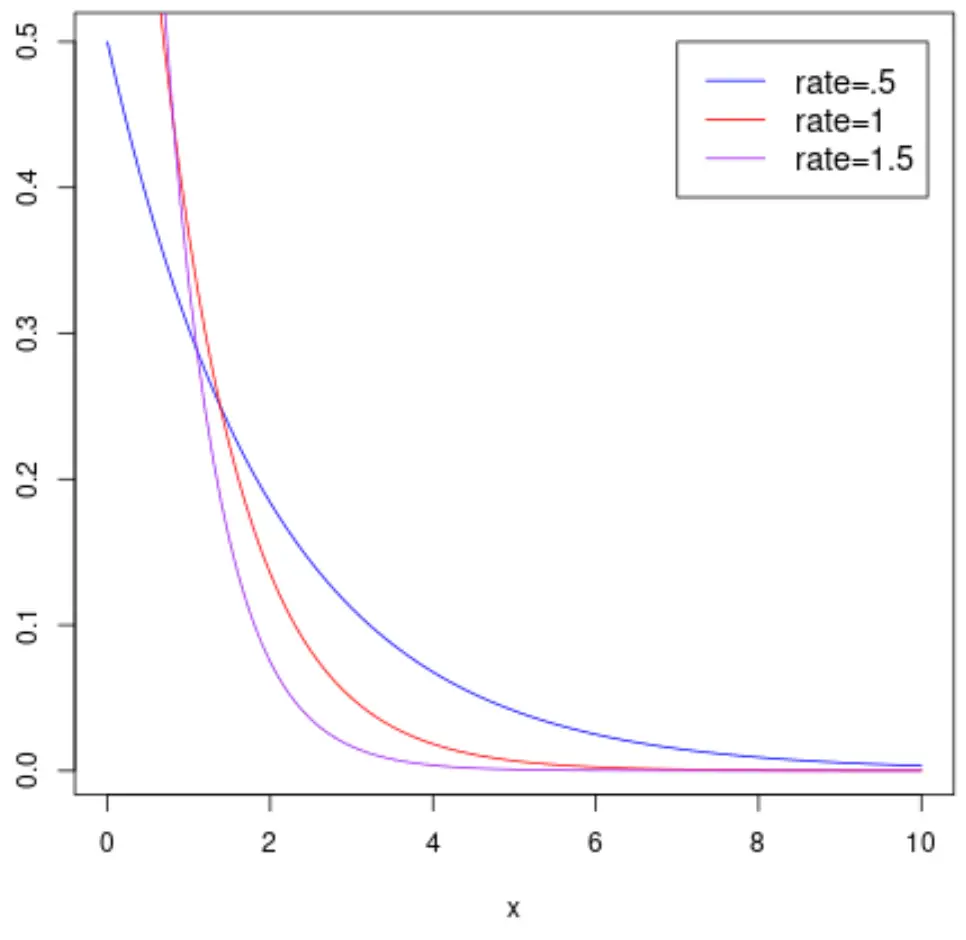
下图显示了随机变量X的累积分布函数，该函数遵循具有不同速率参数的指数分布：

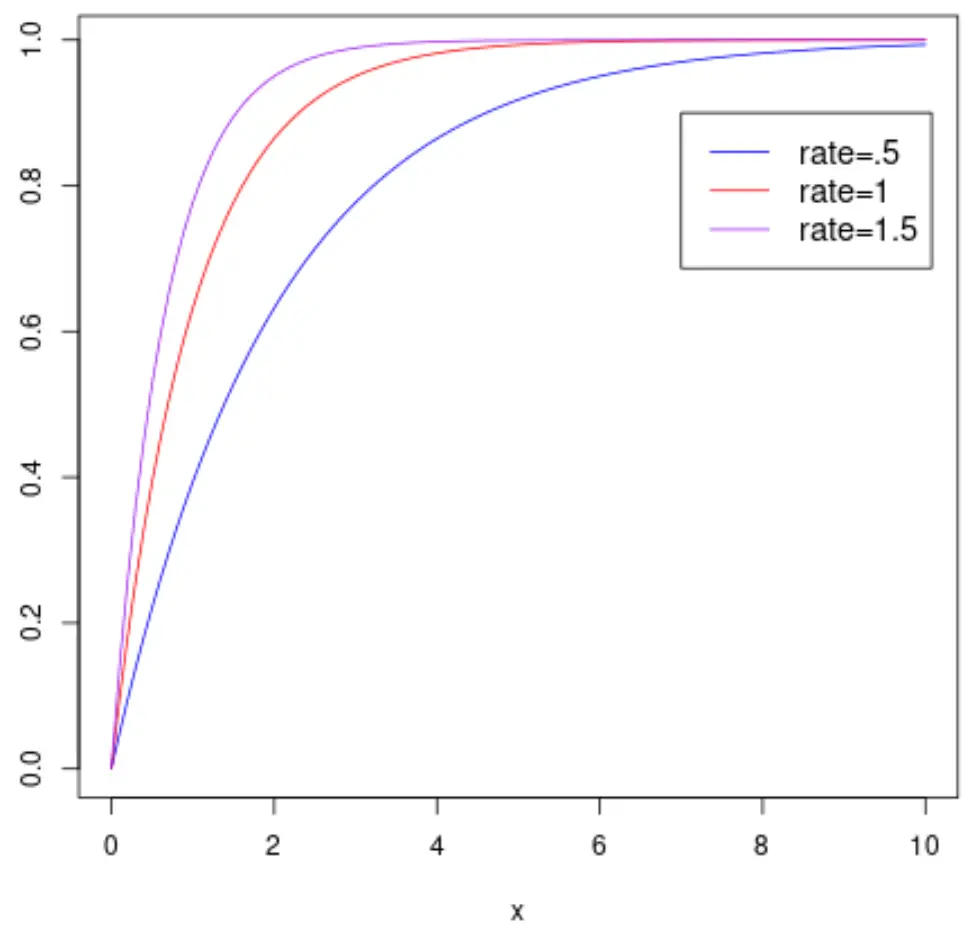
注意：查看本教程以了解如何在 R 中绘制指数分布。

指数分布的性质

指数分布具有以下性质：

• 平均值： 1 / λ
• 差值： 1 / λ ²

例如，假设某个间歇泉喷发之间的平均分钟数为 40 分钟。我们将比率计算为 λ = 1/μ = 1/40 = 0.025。

然后我们可以计算该分布的以下属性：

• 下次喷发的平均等待时间：1/λ = 1 /.025 = 40
• 下一次喷发的等待时间变化：1/λ ² = 1 /.025 ² = 1600

注意：指数分布还具有无记忆特性，即未来事件发生的概率不受过去事件发生的影响。

指数分布练习题

使用以下练习题来测试您对指数分布的了解。

问题1：平均每两分钟就有一位新顾客进入一家商店。客户到达后，确定新客户在一分钟内到达的概率。

解决方案 1：客户端之间的平均时间为两分钟。因此，该比率可以计算如下：

• λ = 1/μ
• λ = 1/2
• λ = 0.5

我们可以将 λ = 0.5 和 x = 1 代入 CDF 公式：

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0.5(1)
• P(X ≤ 1) = 0.3935

我们需要等待不到一分钟才能下一位顾客到达的概率是0.3935 。

问题2：某个地区平均每400天就会发生一次地震。地震发生后，确定距离下一次地震发生 500 天以上的概率。

解2：地震的平均间隔时间是400天。因此，该比率可以计算如下：

• λ = 1/μ
• λ = 1/400
• λ = 0.0025

我们可以将 λ = 0.0025 和 x = 500 代入 CDF 公式：

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0.0025(500)
• P(X≤1)=0.7135

下一次地震需要等待不到 500 天的概率是 0.7135。因此，我们需要等待 500 天以上才能发生下一次地震的概率是 1 – 0.7135 = 0.2865 。

问题 3：呼叫中心平均每 10 分钟就会接到一个新呼叫。客户致电后，确定新客户在 10 到 15 分钟内致电的可能性。

解决方案 3：呼叫之间的平均时间为 10 分钟。因此，该比率可以计算如下：

• λ = 1/μ
• λ = 1/10
• λ = 0.1

我们可以使用以下公式来计算新客户在 10-15 分钟内致电的概率：

• P(10 < X ≤ 15) = (1 – e ^-0.1(15) ) – (1 – e ^-0.1(10) )
• P(10 < X ≤ 15) = 0.7769 – 0.6321
• P(10 < X ≤ 15) = 0.1448

新客户在 10-15 分钟内致电的可能性。是0.1448 。

其他资源

以下教程介绍了其他常见的概率分布。

正态分布简介
二项分布简介
泊松分布简介
均匀分布简介