如何在 r 中应用中心极限定理（附示例）

中心极限定理指出，如果样本量足够大，即使总体分布不正态，样本均值的抽样分布也近似正态。

中心极限定理还指出，抽样分布将具有以下属性：

1.抽样分布的均值将等于总体分布的均值：

x = µ

2.抽样分布的标准差等于总体分布的标准差除以样本量：

s = σ /n

以下示例展示了如何在 R 中应用中心极限定理。

示例：中心极限定理在 R 中的应用

假设乌龟壳的宽度服从均匀分布，最小宽度为 2 英寸，最大宽度为 6 英寸。

也就是说，如果我们随机选择一只乌龟并测量它的壳的宽度，它也很可能在 2 到 6 英寸宽之间。

以下代码演示了如何在 R 中创建一个数据集，其中包含 1,000 只海龟的甲壳宽度测量值，均匀分布在 2 到 6 英寸之间：

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

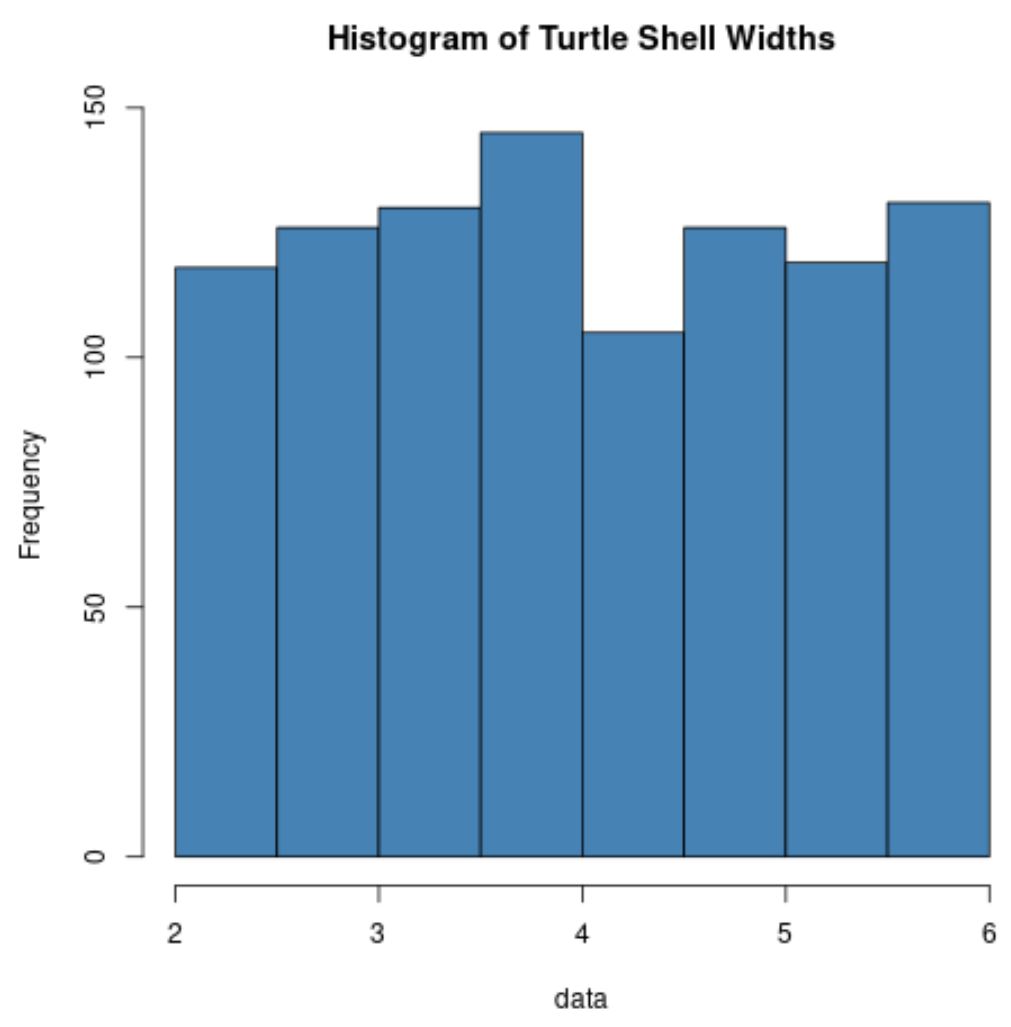
请注意，龟壳宽度的分布通常根本不分布。

现在想象一下，我们从这个种群中重复随机抽取 5 只海龟样本，并一遍又一遍地测量样本平均值。

以下代码展示了如何在 R 中执行此过程并创建直方图以可视化样本均值的分布：

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

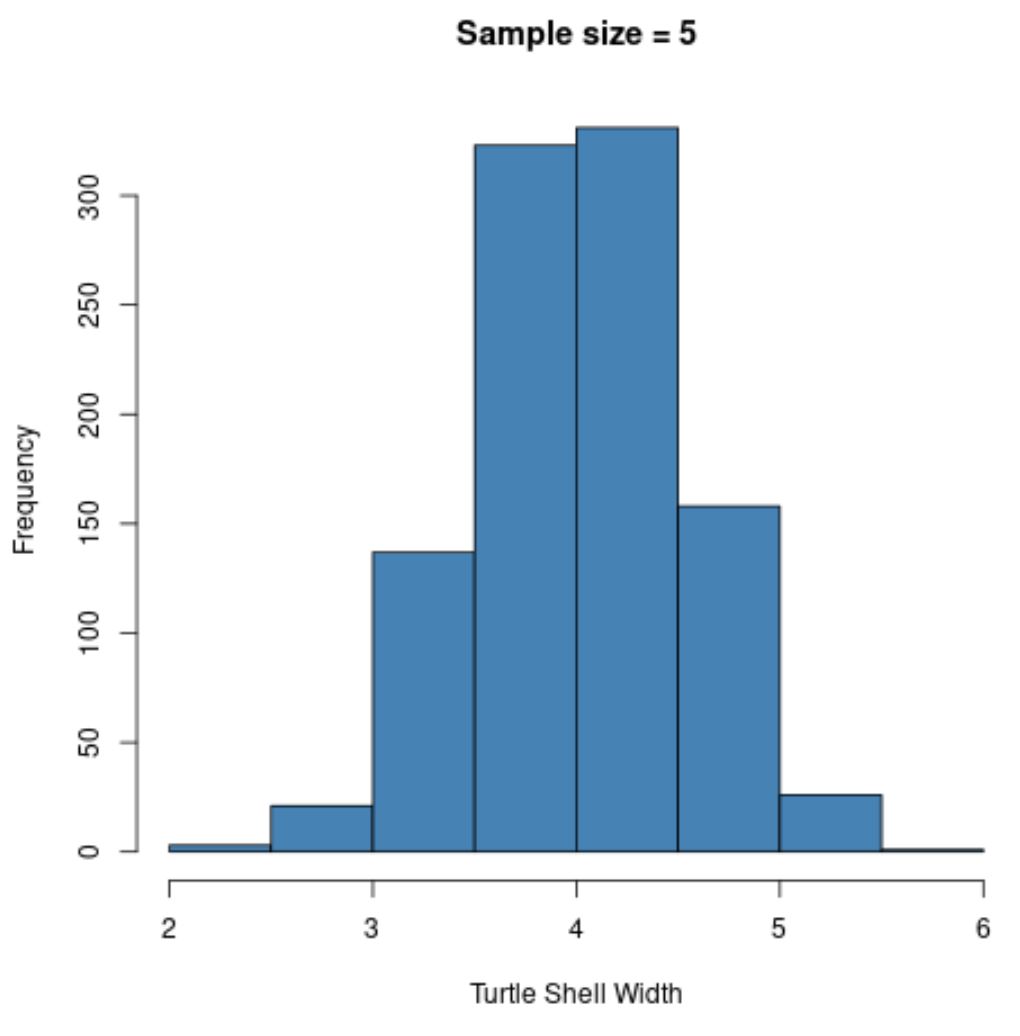
请注意，样本均值的抽样分布显示为正态分布，即使样本来源的分布不是正态分布。

另请注意此抽样分布的样本均值和样本标准差：

• x̄ ：4.008
• s ：0.517

现在假设我们将使用的样本量从 n=5 增加到 n=30 并重新创建样本均值的直方图：

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

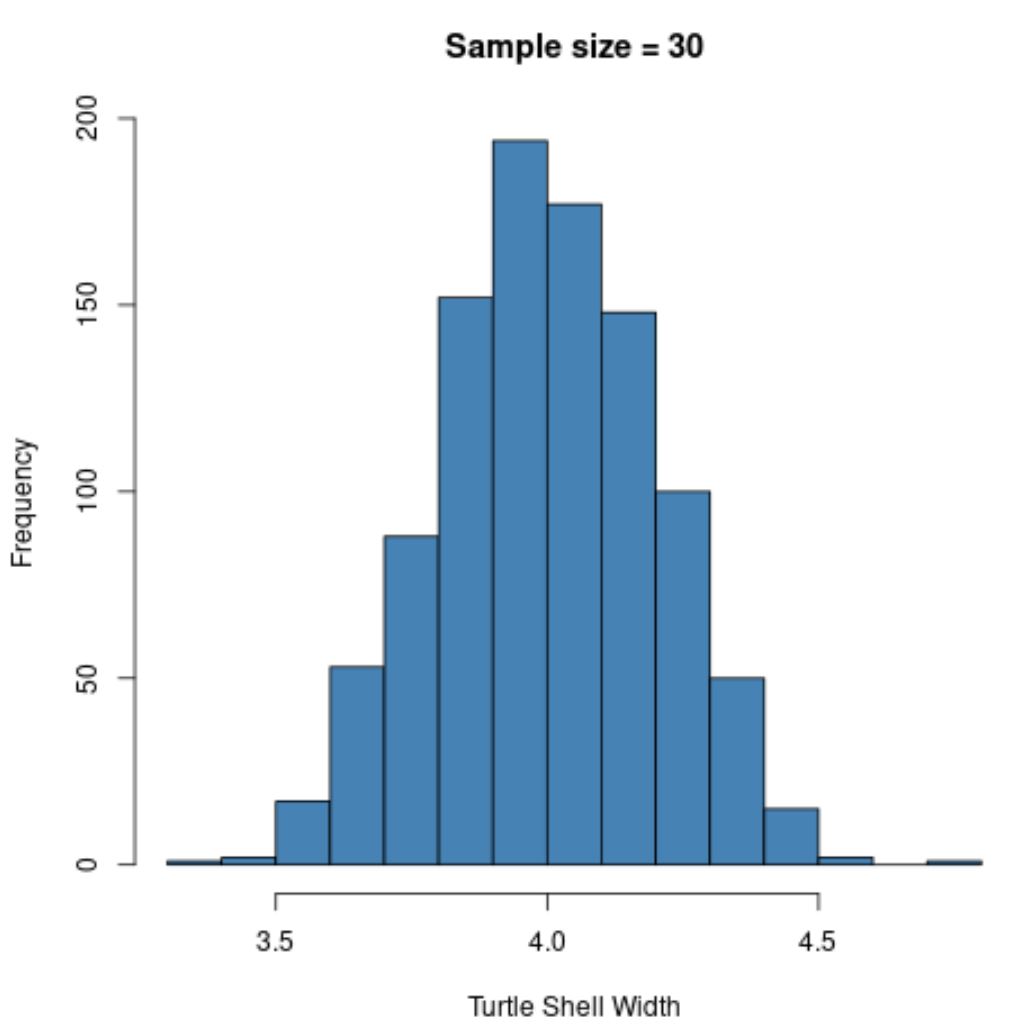
抽样分布仍然是正态分布，但样本标准差更小：

• s ：0.200

这是因为与前面的示例 (n=5) 相比，我们使用了更大的样本量 (n=30)，因此样本均值的标准差甚至更小。

如果我们继续使用越来越大的样本，我们会发现样本标准差变得越来越小。

这说明了实践中的中心极限定理。

其他资源

以下资源提供了有关中心极限定理的更多信息：

中心极限定理简介
中心极限定理计算器
中心极限定理在现实生活中应用的 5 个例子