什么是回归器？ （定义和示例）
在统计学中，回归量是用于预测响应变量的回归模型中任何变量的名称。
回归器也称为：
所有这些术语都可以互换使用，具体取决于您所从事的领域类型：统计学、机器学习、计量经济学、生物学等。
注意：有时响应变量被称为“可回归”。
回归模型中的回归量
大多数回归模型采用以下形式：
Y = β 0 + B 1 x 1 + B 2 x 2 + B 3 x 3 + ε
金子：
- Y：响应变量
- β i ：回归量的系数
- x i ：回归量
- ε：误差项
构建回归模型的目的是了解回归量的变化如何导致响应变量（或“回归量”）的变化。
请注意，回归模型可以有一个或多个回归量。
当只有一个回归量时，该模型称为简单线性回归模型，当有多个回归量时，该模型称为多元线性回归模型，以表明存在多个回归量。
以下示例说明了如何解释不同回归模型中的回归量。
示例 1：农作物产量
假设农民想要了解影响农作物总产量（以磅为单位）的因素。它收集数据并构建以下回归模型：
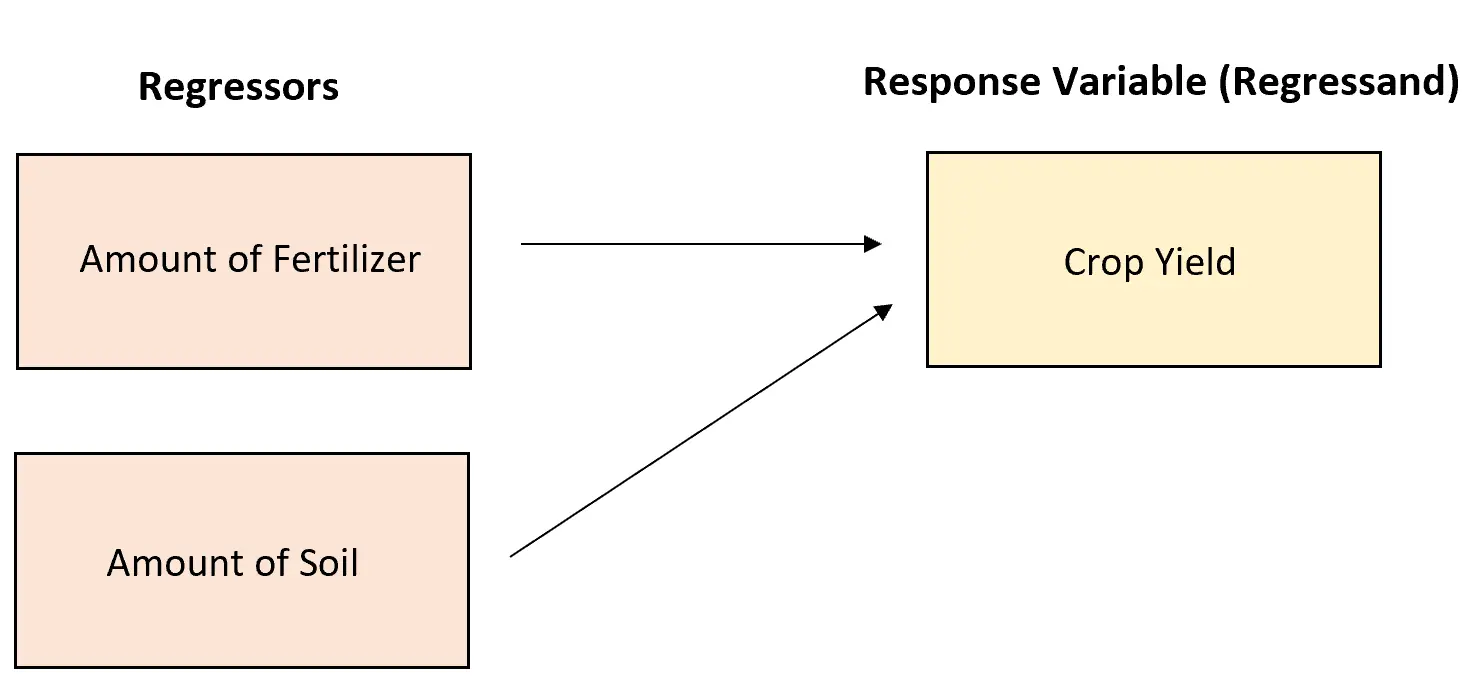
作物产量 = 154.34 + 3.56*（肥料磅数）+ 1.89*（土壤磅数）
该模型有两个回归量：肥料和土壤。
以下是如何解释这两个回归量：
- 肥料：假设土壤量保持不变，每增加一磅肥料，作物产量平均增加 3.56 磅。
- 土壤：假设肥料用量保持不变，每增加一磅土壤，作物产量平均增加 1.89 磅。
示例 2：考试结果
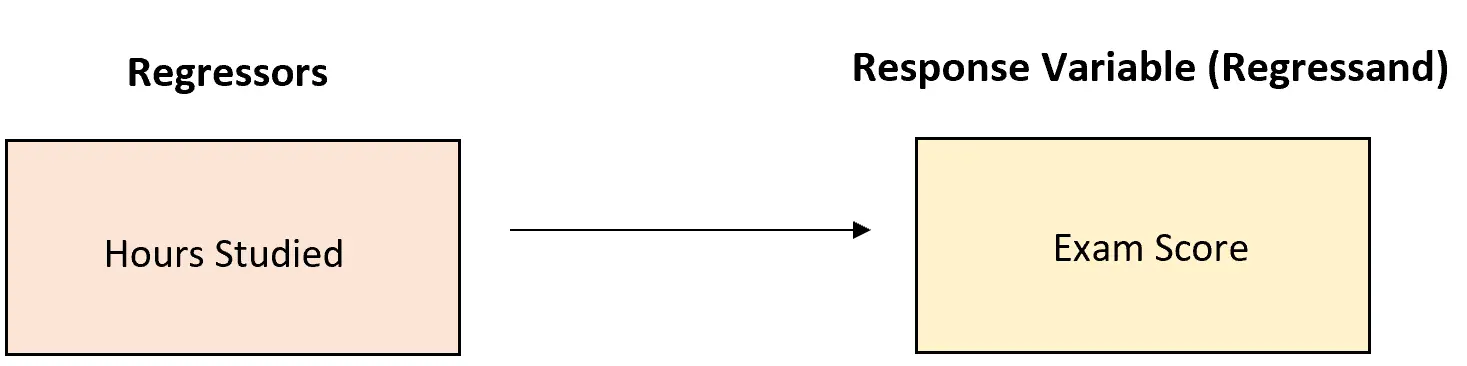
假设一位教授想要了解学习时数如何影响考试成绩。它收集数据并构建以下回归模型：
考试成绩 = 68.34 + 3.44*（学习时间）
该模型包括一个回归量：学习时间。我们将此回归系数解释为：每多学习一小时，考试成绩平均就会增加 3.44 分。
其他资源
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多