什么是多项式检验？ （定义&#038；示例）

多项式检验用于确定分类变量是否遵循假设分布。

该检验使用以下原假设和备择假设：

H ₀ ：分类变量遵循假设分布。

H _A ：分类变量不遵循假设分布。

如果检验的p 值低于一定的显着性水平（例如 α = 0.05），那么我们可以拒绝零假设并得出结论：变量不遵循假设的分布。

当变量可以得出k 个不同的结果时，使用此测试。多项式测试的一个典型例子是我们想要确定某些骰子是否公平。当您掷骰子时，它落在每个数字（1 到 6）上的概率是 1/6。

为了测试骰子是否公平，我们可能会滚动它多次，看看它落在不同数字上的次数是否与我们预期的有显着差异。

以下示例演示如何使用 R 统计编程语言执行多项式检验。

示例 1：公平骰子

假设我们想确定骰子是否公平。为了测试这一点，我们运行了 30 次并记录每个结果的频率。下表显示了结果：

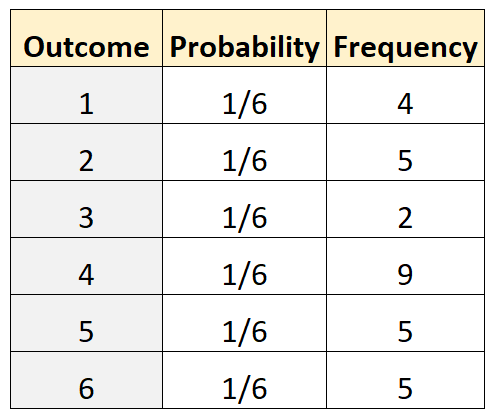
R 中的以下代码可用于执行多项式测试：

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

检验的 p 值为0.4306 。由于该 p 值不小于 0.05，因此我们不会拒绝原假设。所以我们没有足够的证据表明骰子不公平。

示例2：产品销售

假设商店老板假设相同数量的顾客将购买四种不同的产品。为了测试这一点，它记录了给定一周内购买每种产品的客户数量。下表显示了结果：

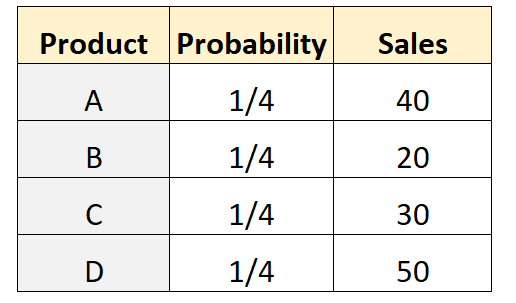
R 中的以下代码可用于对此数据集执行多项式测试：

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

检验的 p 值为0.00226 。由于该 p 值小于 0.05，因此我们将拒绝原假设。因此，我们有足够的证据表明每种产品的销售额并不相同。

示例 3：袋子里的弹珠

汤姆指出，从袋子中选择红色、绿色或紫色弹珠的概率分别为 0.2、0.5 和 0.3。为了测试这一点，他的朋友迈克把手伸进袋子里，取出一颗弹珠（以及替换的弹珠）100 次。下表显示了结果：

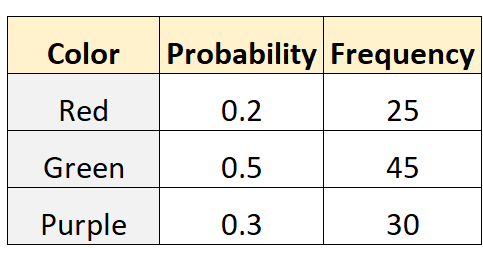
R 中的以下代码可用于对此数据集执行多项式测试：

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

检验的 p 值为0.3999 。由于该 p 值不小于 0.05，因此我们将无法拒绝原假设。因此，我们没有足够的证据表明袋子中弹珠的分布与汤姆指定的不同。

其他资源

多项式分布简介
多项分布计算器