峰度可以为负吗？

在统计学中，峰度用于描述概率分布的形状。

具体来说，它告诉我们数据值在分布的尾部或顶部聚集的程度。

分布的峰度可以是负值、零或正值。

零峭度

如果分布的峰度为 0，则它等于具有以下钟形形状的正态分布：

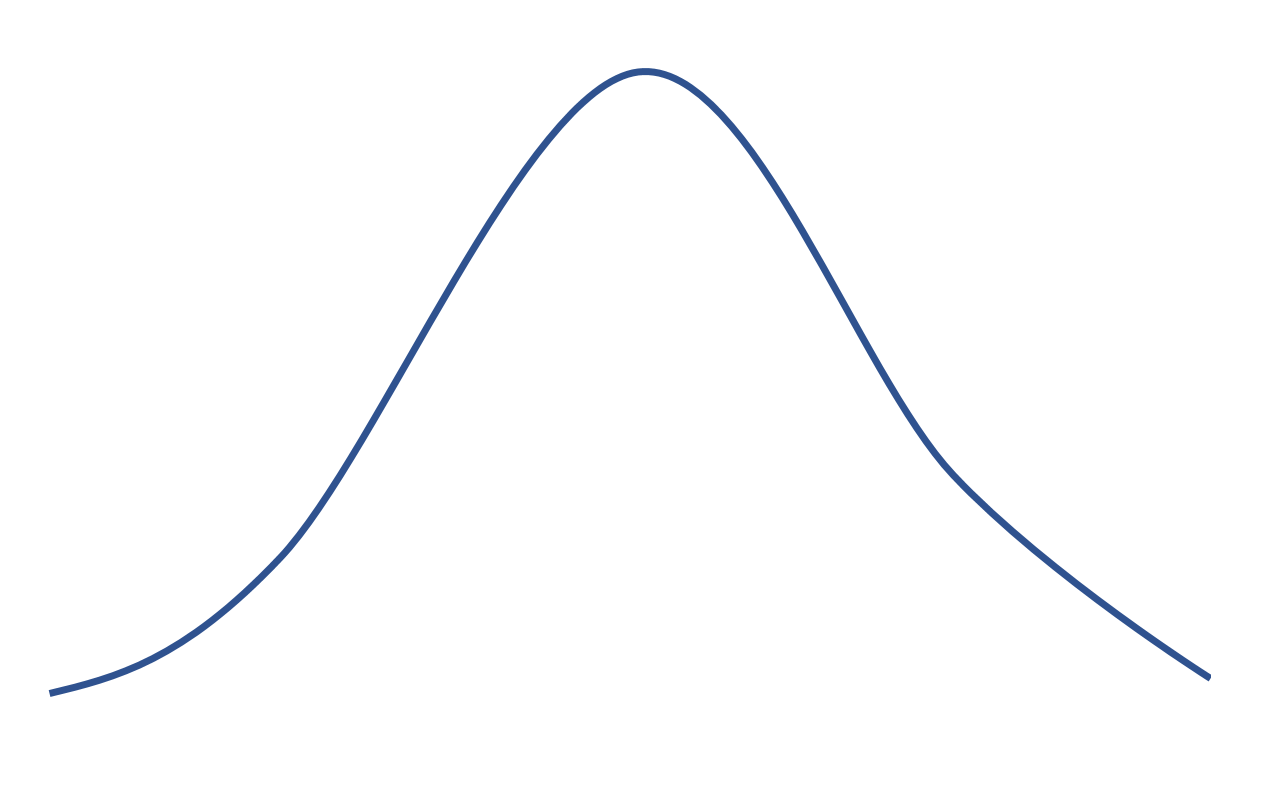
正峰度

如果分布具有正峰度，则称为尖峰型，这意味着与正态分布相比，它具有更尖锐的峰值和更重的尾部。

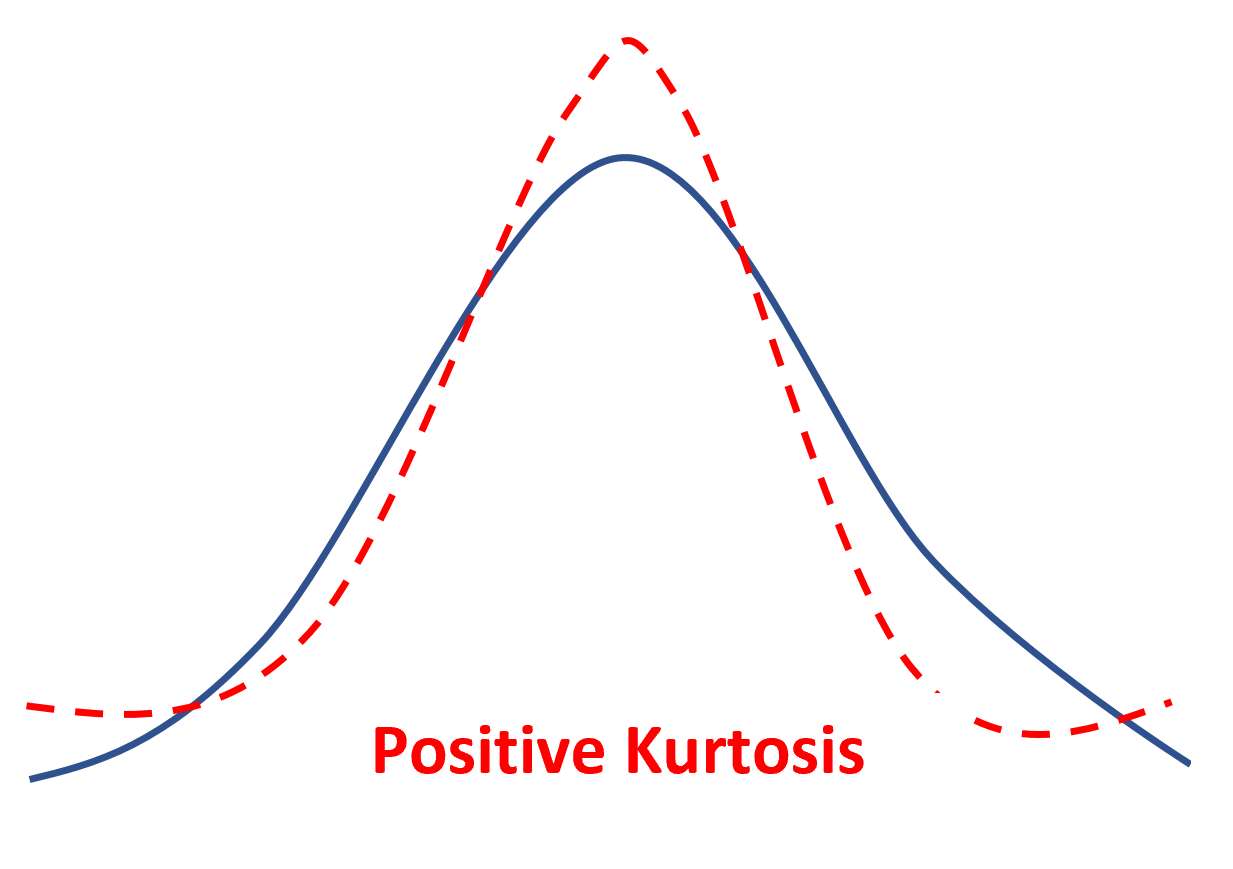
这仅仅意味着更少的数据值位于平均值附近，更多的数据值位于尾部。

最著名的正峰度分布是 t 分布，与正态分布相比，它具有更尖锐的峰值和更重的尾部。

负峰度

如果分布具有负峰度，则称为platykurtic ，这意味着与正态分布相比，它具有更平坦的峰值和更细的尾部。

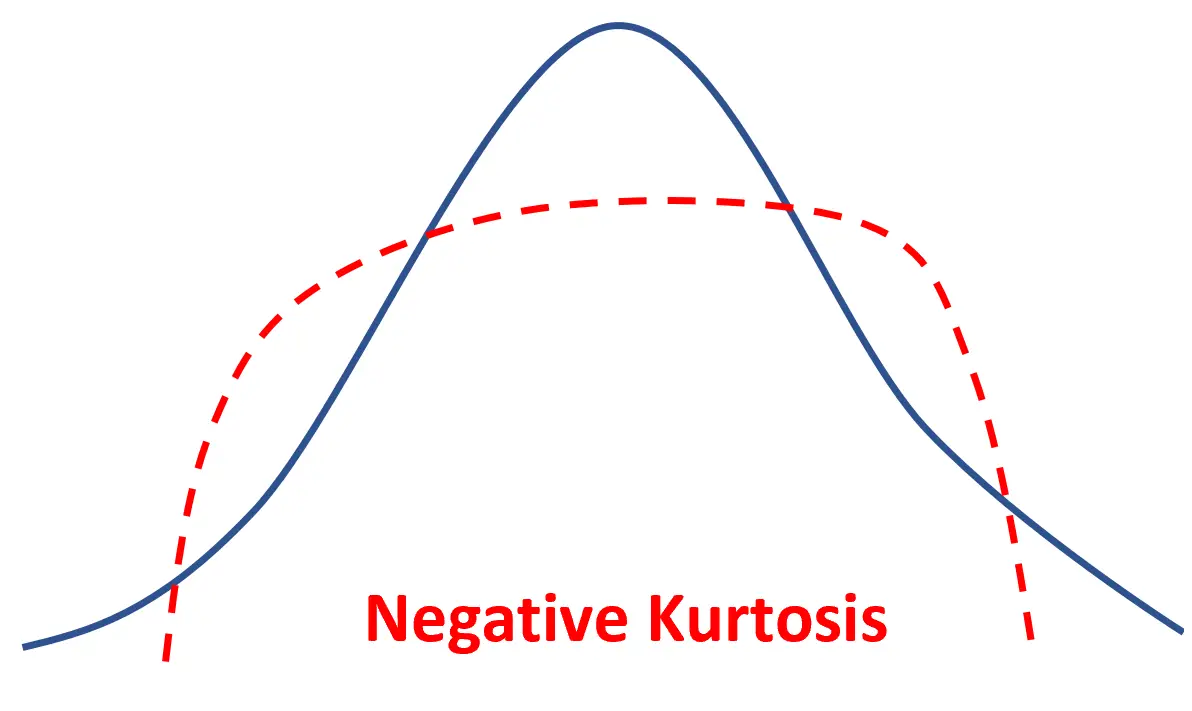
这仅仅意味着更多的数据值位于均值附近，而更少的数据值位于尾部。

表现出负峰度的分布的一个极端例子是均匀分布，它没有峰值并且是完全平坦的分布。

在实践中何时使用奉承

在实践中，当我们只是想更好地理解数据时，我们经常在分析的探索阶段测量分布的峰度。

因此，如果我们看到峰度为正，我们就知道我们正在处理的分布中，靠近中心的数据值较少，而沿尾部分布的数据值较多。

相反，如果我们看到峰度为负，我们就知道我们正在处理的分布中，靠近中心的数据值较多，而尾部的数据值较少。

其他资源

要查找给定分布的偏度和峰度，您可以将原始数据值输入到此偏度和峰度计算器中，它将告诉您分布的偏度和峰度。

用于确定特定分布是否表现出与正态分布相对应的偏度和峰度的最流行的统计测试之一是Jarque Bera 测试。

可汗学院还有一系列精彩的视频，介绍如何对分布形状进行分类。