描述性统计或推论性统计:有什么区别?
统计领域有两个主要分支:
- 描述性统计
- 推论统计
本教程解释了这两个分支之间的区别以及为什么每个分支在某些情况下都很有用。
描述性统计
简而言之,描述性统计旨在使用汇总统计、图表和表格来描述一组原始数据。
描述性统计非常有用,因为它们可以让您比仅仅查看一行又一行的原始数据值更快、更轻松地理解一组数据。
例如,假设我们有一个原始数据集,显示特定学校 1,000 名学生的测试成绩。我们可能对平均测试分数以及测试分数的分布感兴趣。
使用描述性统计,我们可以找到平均分数并创建一个图表来帮助我们可视化分数的分布。
这使我们能够比仅仅查看原始数据更容易地了解学生的考试成绩。
描述性统计的常见形式
描述性统计有以下三种常见形式:
1、汇总统计。这些是使用单个数字汇总数据的统计数据。有两种常见的汇总统计类型:
- 集中趋势的度量:这些数字描述了数据集的中心在哪里。示例包括平均 和中位数.
- 分散度度量:这些数字描述了数据集中值的分布。示例包括区间、四分位距、标准差和方差。
2.图形。图表帮助我们可视化数据。用于可视化数据的常见图表类型包括 箱线图、 直方图、 茎叶图和散点图。
3. 表格。表格可以帮助我们了解数据是如何分布的。常见的表类型是频率表,它告诉我们有多少数据值落在特定范围内。
使用描述性统计的示例
以下示例说明了我们如何在现实世界中使用描述性统计。
假设某所学校的 1,000 名学生都参加相同的考试。我们想要了解测试结果的分布,因此我们使用以下描述性统计:
1. 汇总统计
平均分:82.13 。这告诉我们,这 1,000 名学生的平均考试成绩是 82.13。
中位数:84。这告诉我们一半的学生得分高于 84,另一半得分低于 84。
最大值:100。最小值:45。这告诉我们,任何学生获得的最高分数是 100,最低分数是 45。范围(告诉我们最大值和最小值之间的差异)是 55。
2. 图形
为了可视化测试结果的分布,我们可以创建直方图——一种使用矩形条表示频率的图表。
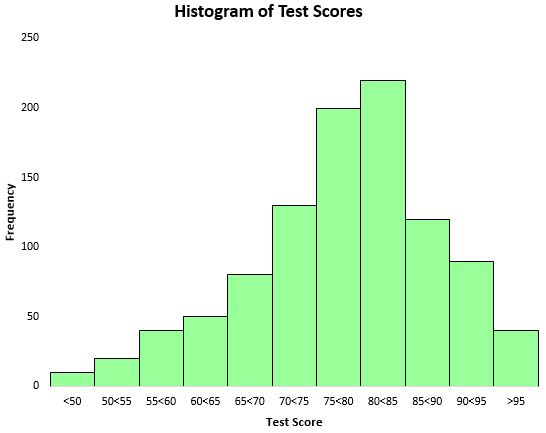
根据这个直方图,我们可以看到测试成绩的分布大致呈钟形。大多数学生的得分在70到90之间,而很少有人得分高于95,得分低于50的则更少。
3. 表格
了解分数分布的另一种简单方法是创建频率表。例如,下面的频率表显示了得分在不同范围之间的学生的百分比:
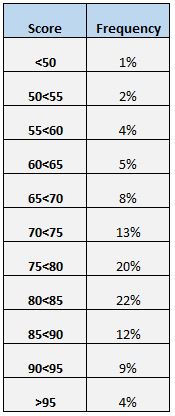
我们可以看到,只有 4% 的学生得分在 95 分以上。我们还可以看到,(12% + 9% + 4% = ) 25% 的学生得分在 85 分或以上。
如果我们想知道数据值高于或低于某个值的百分比是多少,则频率表特别有用。例如,假设学校认为“可接受”的考试成绩是任何高于 75 分的成绩。
查看频率表,我们可以很容易地看到 (20% + 22% + 12% + 9% + 4% = ) 67% 的学生在测试中获得了可接受的分数。
推论统计
简而言之,推论统计使用小数据样本来得出有关样本较大总体的结论。
例如,我们可能想了解一个国家数百万人的政治偏好。
然而,对全国每个人进行调查将过于耗时且昂贵。因此,我们会进行一项较小规模的调查,例如,针对 1,000 名美国人,并利用调查结果得出有关总体人口的结论。
这是推论统计的整个前提:我们想要回答有关总体的问题,因此我们获取该总体的一小部分样本的数据,并使用样本数据来得出有关总体的推论。
代表性样本的重要性
为了对我们使用样本得出关于总体的结论的能力充满信心,我们必须确保我们有一个具有代表性的样本,即总体中个体的特征与样本紧密匹配的样本特征。占总人口的比例。
理想情况下,我们希望我们的样本类似于我们总体的“迷你版”。因此,如果我们想对由 50% 女孩和 50% 男孩组成的学生群体得出结论,如果我们的样本包括 90% 男孩和仅 10% 女孩,那么我们的样本将不具有代表性。

如果我们的样本与总体总体不相似,我们就无法自信地将样本结果推广到总体总体。
如何获得有代表性的样本
为了最大限度地提高获得代表性样本的机会,您应该关注两件事:
1. 确保使用随机抽样方法。
您可以使用多种可能产生代表性样本的随机抽样方法,包括:
- 简单的随机样本
- 系统随机样本
- 整群随机样本
- 分层随机样本
随机抽样方法往往会产生具有代表性的样本,因为总体中的每个成员都有平等的机会被包含在样本中。
2. 确保您的样本量足够大。
除了使用适当的抽样方法之外,确保样本足够大也很重要,以便您有足够的数据能够推广到更大的总体。
要确定样本量,您需要考虑正在研究的总体规模、要使用的置信水平以及您认为可接受的误差范围。
幸运的是,您可以使用在线计算器输入这些值并查看您的样本量应该是多少。
推论统计的常见形式
推论统计有三种常见形式:
1.假设检验。
我们经常想回答有关人群的问题,例如:
- 俄亥俄州支持候选人 A 的民众比例是否超过 50%?
- 某种植物的平均高度等于 14 英寸吗?
- A学校和B学校学生的平均身高有差异吗?
为了回答这些问题,我们可以进行假设检验,这使我们能够使用样本中的数据得出有关总体的结论。
2. 置信区间。
有时我们想要估计总体的某个值。例如,我们可能对澳大利亚某些植物物种的平均高度感兴趣。
我们可以收集一小部分植物样本并测量每一种植物,而不是四处走动并测量该国的每一株植物。然后我们可以使用样本中植物的平均高度来估计种群的平均高度。
然而,我们的样本不太可能提供完美的人口估计。幸运的是,我们可以通过创建置信区间来解释这种不确定性,该区间提供了一系列值,我们确信真实的总体参数位于其中。
例如,我们可以生成 [13.2, 14.8] 的 95% 置信区间,这意味着我们 95% 确定该植物物种的真实平均高度在 13.2 英寸到 14.8 英寸之间。
3.回归。
有时我们想了解总体中两个变量之间的关系。
例如,假设我们想知道每周学习的时间是否与考试成绩相关。为了回答这个问题,我们可以执行一种称为回归分析的技术。
因此,我们可以查看 100 名学生的学习小时数和考试成绩,并进行回归分析,看看这两个变量之间是否存在显着关系。
如果发现回归的 p 值显着,那么我们可以得出结论,在整个学生群体中这两个变量之间存在显着关系。
描述性统计和推论性统计之间的区别
总之,描述性统计和推论性统计之间的区别可以描述如下:
描述性统计使用汇总统计、图表和表格来描述一组数据。
这对于帮助我们快速轻松地理解一组数据非常有用,而无需遍历所有单独的数据值。
推论统计使用样本得出有关较大群体的结论。
根据您想要回答的有关总体的问题,您可以决定使用以下一种或多种方法:假设检验、置信区间和回归分析。
如果您选择使用其中一种方法,请记住您的样本必须能够代表您的总体,否则您得出的结论将不可靠。