样本量
本文解释了什么是样本量以及它在统计学中的重要性。此外,您还将了解如何计算适当的样本量和已解决的练习,以便您了解它是如何完成的。
样本量是多少?
样本量(或样本量)是构成研究样本的个体数量。在统计学中,样本量很重要,这样样本才能代表整个总体。
因此,统计研究的样本量必须足够大,才能代表整个人群的特征。另一方面,样本量不能太大,因为这样研究就会变得更加昂贵。总之,样本量要充足,不能太大也不能太小。
例如,如果我们想对一个国家的身高进行分析,我们不能要求该国所有居民的身高,因为测量时间会很长,而且成本太高。因此,有必要进行随机抽样并仅采访总体中具有代表性的样本。
我们如何知道合适的样本量?在下一节中,我们将了解如何根据研究要求确定合适的样本量。
如何计算样本量
为了估计平均值,所需的样本量等于 Z α/2的平方乘以标准差 (σ) 再除以所需的误差幅度 (e)。因此,计算样本量的公式为:
![]()
金子:
-

是样本大小。
-
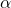
是所需的显着性水平。考虑到这一点
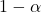
是所需的置信水平。
-

是对应于 α/2 概率的标准正态分布的分位数。对于大样本量和 95% 置信水平,它通常接近 1.96;对于 99% 置信水平,它通常接近 2.576。
-

是标准差。
请记住,在此公式中假设人口规模是无限的,即人口规模非常大或未知。
注:上式是从平均值 的置信区间公式推导出来的。
样本量计算示例
在本节中,我们将以计算统计调查的适当样本量为例。
- 我们知道总体的标准差约为 15,但我们不知道其平均值,因此我们想要进行一项研究来估计平均值。如果我们想要 ±2 的误差幅度和 95% 的置信水平,我们需要多大的样本量?
正如我们在上面看到的,计算样本量的公式是:
![]()
在这种情况下,所需的置信水平为 95%,因此相应的 Z α/2值为 1.96。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
最后,既然我们知道了所有参数的值,我们将它们的值代入公式并计算样本量:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dd8e2d30042f759051fb52c5c55ade44_l3.png)
简而言之,为了根据期望的要求估计总体平均值,我们至少需要 217 个人的样本。
样本量、置信水平和误差幅度
根据所需的置信水平和误差幅度,所需的样本量会有所不同。因此,样本量、置信度和误差幅度之间的关系如下:
- 样本量和置信度成正比。也就是说,如果置信水平增加,样本量也会增加。
- 样本量和误差幅度成反比。因此,如果误差幅度增加,样本量就会减少。
- 因此,增加样本量可以提高置信水平或减少误差幅度。
其他样本量公式
根据要估计的参数,所需样本量的公式略有不同。因此,在本节中,我们将看到在某些特殊情况下可用于计算样本量的其他公式。
比例的样本量
估计比例 (p) 所需样本量的计算公式为:
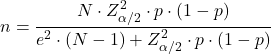
概率的样本量
当您想要估计概率时,建议使用以下公式来确定必要的样本量:
![]()
用于比较两个独立平均值的样本量
在给定 α 风险和 β 风险的情况下比较两个独立均值时计算样本量的公式如下:
![]()
金子
![]()
是备择假设的两种均值之间的差异。
用于比较两个配对均值的样本量
如果要比较具有固定误差 α 和误差 β 的两个配对均值,则用于查找样本中观测值数量的公式为:
![]()
金子
![]()
是备择假设的两个配对均值之间的差异,
![]()
它是同一个体的两次测量之间的差异的方差。