正态分布或均匀分布：有什么区别？

正态分布是统计学中最常用的概率分布。

它具有以下属性：

• 对称
• 钟形

如果我们创建正态分布图，它将如下所示：

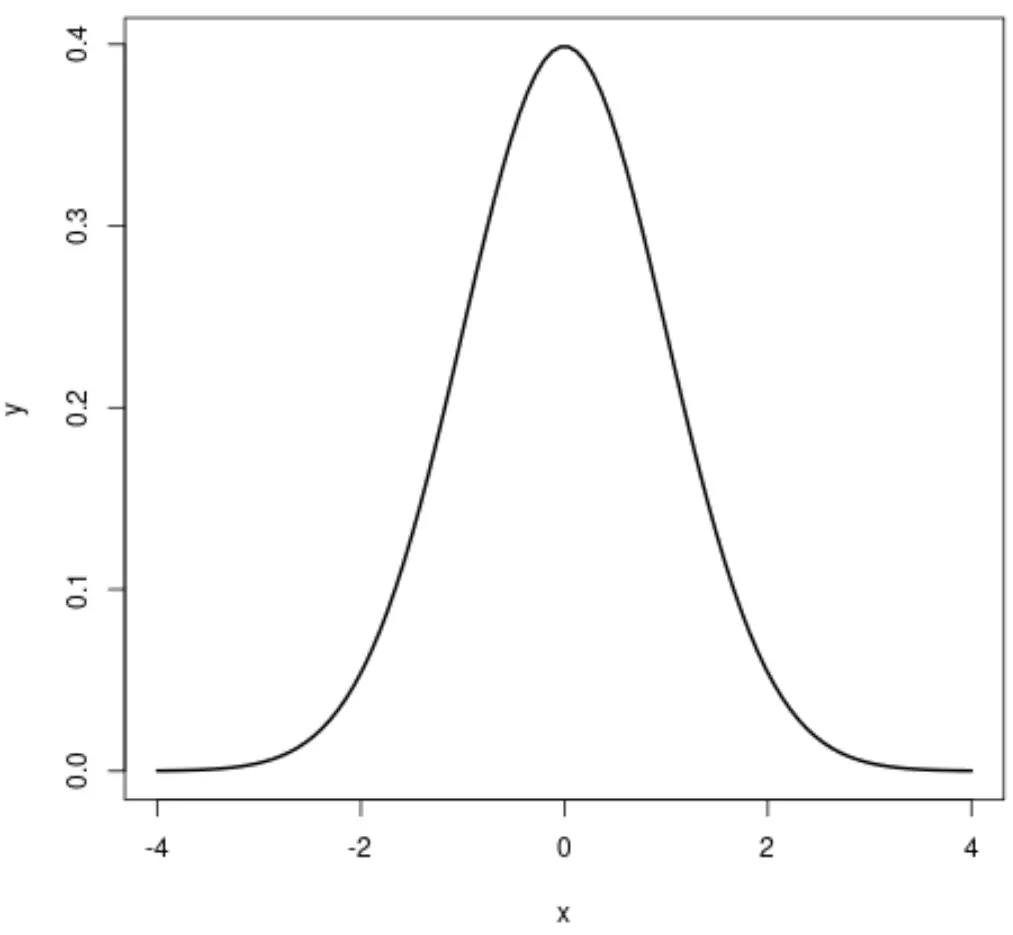
均匀分布是a到b区间内的每个值出现的概率相同的概率分布。

它具有以下属性：

• 对称
• 形状为长方形

如果我们创建均匀分布图，它将如下所示：

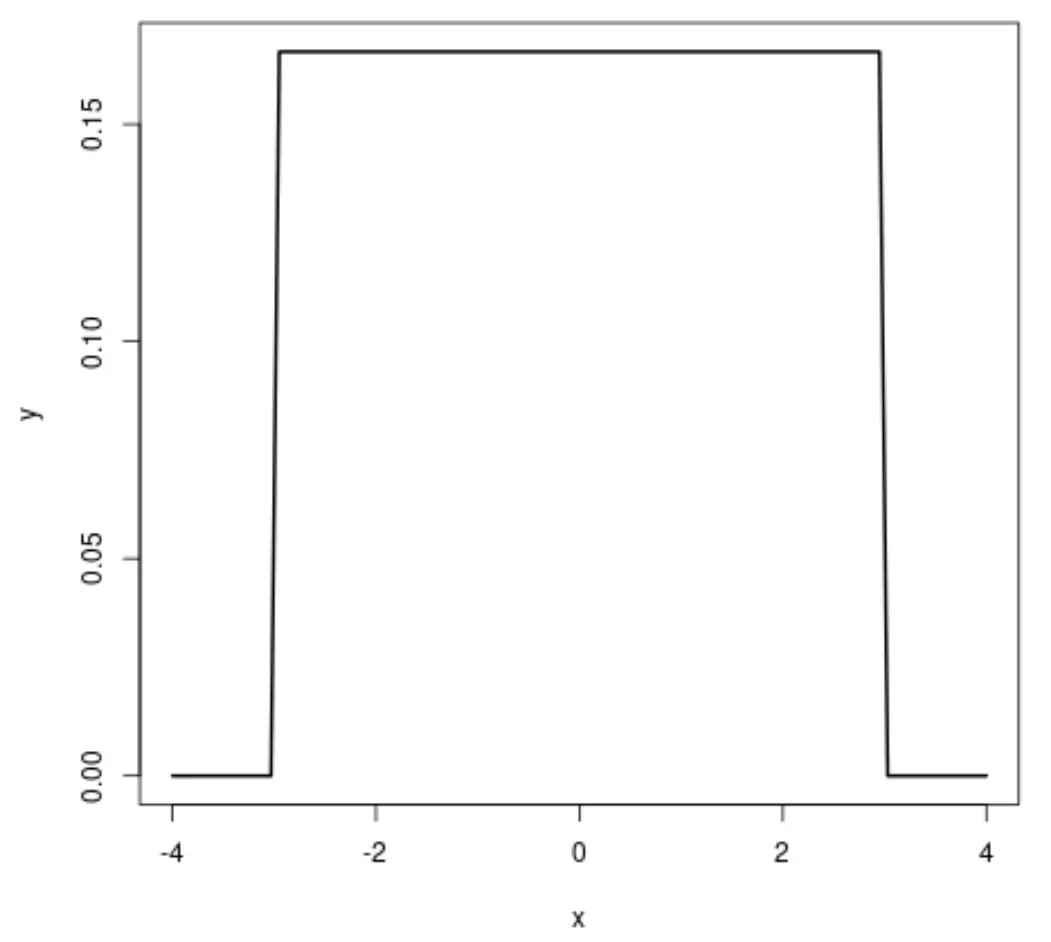
正态分布和均匀分布有以下相似之处：

• 两个分布是对称的。也就是说，如果我们通过分布的中心画一条线，分布的左侧和右侧将完美地相互镜像：

然而，这两个发行版有以下区别：

• 分布具有不同的形状。
• 正态分布是钟形的，这意味着分布中心附近的值比分布尾部的值更有可能出现。
• 均匀分布是矩形的，这意味着分布中的每个值都有相同的出现概率。

正态分布或均匀分布：何时使用它们？

正态分布用于对倾向于遵循“钟形曲线”形状的现象进行建模。例如，有据可查的是，新生儿的出生体重呈正态分布，平均约为 7.5 磅。

美国新生儿出生体重的直方图呈钟形，通常符合正态分布：

大多数婴儿的体重可能在 7.5 磅左右，有一些体重低于 7 磅，有一些体重超过 8 磅。

相反，均匀分布用于对每个潜在结果均等可能的场景进行建模。

一个典型的例子是掷骰子。如果掷一次骰子，它落在 1 到 6 之间的数字上的概率遵循均匀分布，因为每个数字出现的概率相同。

例如，骰子可能落在 6 个数字上，因此掷出 1 的概率为 1/6。

同样，您掷出 2 的概率是 1/6。

同样，你掷出 3 的概率是 1/6。

等等。

奖励：如何绘制正态分布和均匀分布

我们在 R 中使用以下代码来创建正态分布和均匀分布图：

 #define x-axis
x <- seq(-4, 4, length=100)

#calculate normal distribution probabilities
y <- dnorm(x)

#plot normal distribution
plot(x, y, type = " l ", lwd = 2 )

#define x-axis
x <- seq(-4, 4, length=100)

#calculate uniform distribution probabilities
y <- dunif(x, min = -3, max = 3)

#plot uniform distribution
plot(x, y, type = " l ", lwd = 2 , xlim = c(-4, 4))

其他资源

正态分布的 6 个具体例子
5个均匀分布的具体例子
对称分布：定义+示例