如何在 r 中使用 fitdistr() 来拟合分布

您可以使用 R 中MASS包中的fitdistr()函数通过最大化似然函数来估计分布的参数。

该函数使用以下基本语法：

fitdistr（x，densefun，…）

金子：

• x ：表示分布值的数值向量
• dendfun ：估计参数的分布

请注意， densefun参数接受以下潜在分布名称： beta 、 cauchy 、 chi-square 、 exponential 、 gamma 、 geometric 、 lognormal 、 logistic 、负二项式、 normal 、 Poisson 、 t和Weibull 。

以下示例展示了如何在实践中使用fitdistr()函数。

示例：如何使用 fitdistr() 函数来拟合 R 中的分布

假设我们使用 R 中的rnorm()函数生成一个由 200 个值组成的服从正态分布的向量：

 #make this example reproducible
set. seeds (1)

#generate sample of 200 observations that follows normal dist with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

我们可以使用hist()函数创建直方图来可视化数据值的分布：

 hist(data, col=' steelblue ')

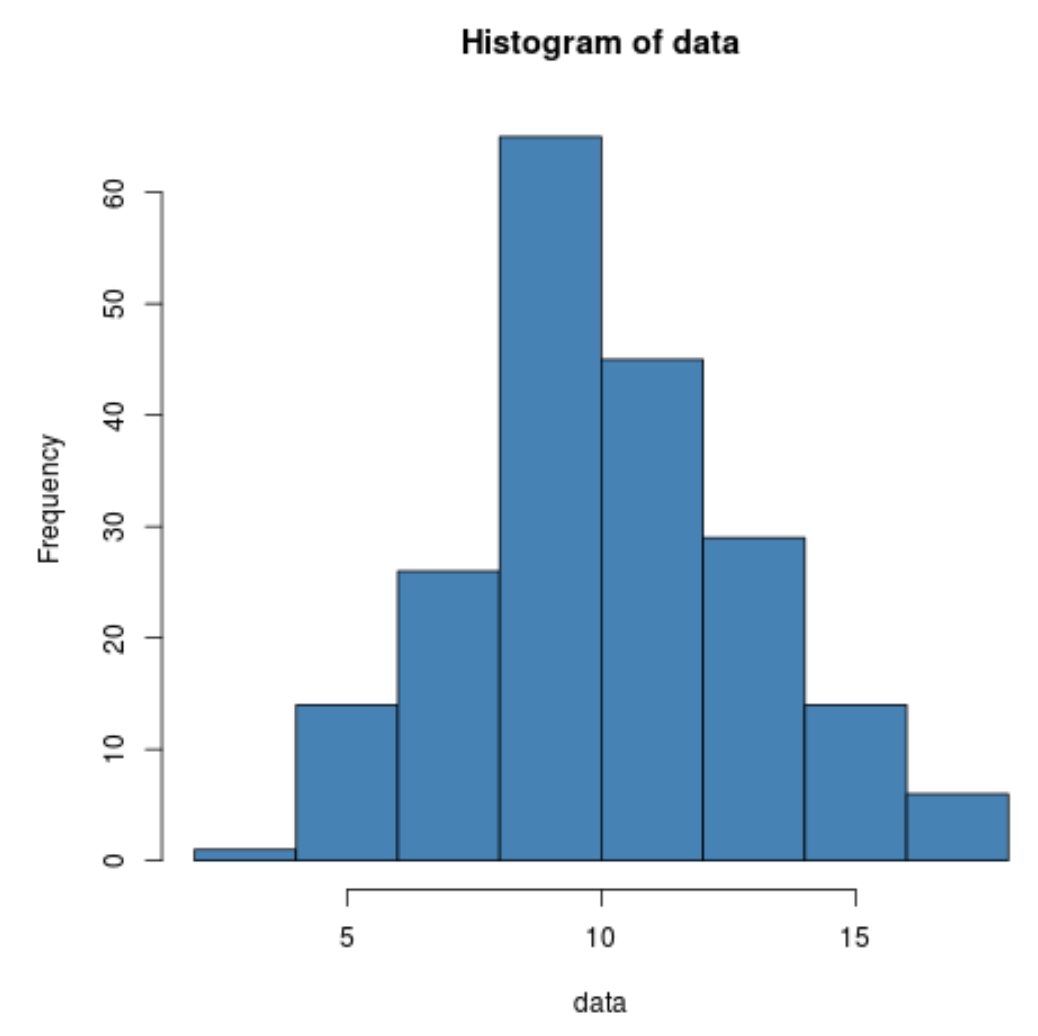
我们可以看到数据确实呈正态分布。

然后我们可以使用fitdistr()函数来估计该分布的参数：

 library (MASS)

#estimate parameters of distribution
fitdistr(data, “ normal ”)

      mean sd    
  10.1066189 2.7803148 
 (0.1965979) (0.1390157)

fitdistr()函数估计值向量服从正态分布，平均值为10.1066189 ，标准差为2.7803148 。

这些值应该不足为奇，因为我们使用rnorm()函数生成数据，平均值为 10，标准差为 3。

其他资源

以下教程解释了如何在 R 中执行其他常见任务：

如何在 R 中绘制正态分布
如何在 R 中生成正态分布
如何在 R 中执行 Shapiro-Wilk 正态性检验