Comment calculer le coefficient de corrélation de Matthews dans R
Le coefficient de corrélation de Matthews (MCC) est une métrique que nous pouvons utiliser pour évaluer les performances d’un modèle de classification .
Il est calculé comme suit :
MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)
où:
- TP : Nombre de vrais positifs
- TN : Nombre de vrais négatifs
- FP : Nombre de faux positifs
- FN : Nombre de faux négatifs
Cette métrique est particulièrement utile lorsque les deux classes sont déséquilibrées, c’est-à-dire qu’une classe apparaît beaucoup plus que l’autre.
La valeur de MCC est comprise entre -1 et 1 où :
- -1 indique un désaccord total entre les classes prédites et les classes réelles
- 0 est synonyme de devinettes complètement aléatoires
- 1 indique un accord total entre les classes prévues et les classes réelles
Par exemple, supposons qu’un analyste sportif utilise un modèle de régression logistique pour prédire si 400 joueurs de basket-ball universitaires différents seront recrutés ou non dans la NBA.
La matrice de confusion suivante résume les prédictions faites par le modèle :
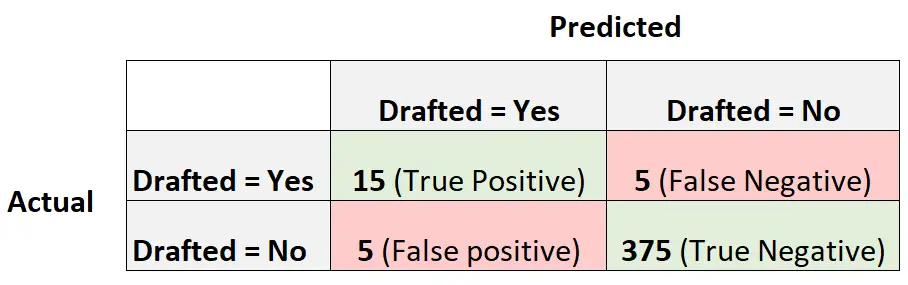
Pour calculer le MCC du modèle, on peut utiliser la formule suivante :
- MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)
- MCC = (15*375-5*5) / √ (15+5)(15+5)(375+5)(375+5)
- MCC = 0,7368
Le coefficient de corrélation de Matthews s’avère être de 0,7368 .
Cette valeur est quelque peu proche de un, ce qui indique que le modèle fait un travail décent pour prédire si les joueurs seront repêchés ou non.
L’exemple suivant montre comment calculer MCC pour ce scénario précis à l’aide de la fonction mcc() du package mltools dans R.
Exemple : Calcul du coefficient de corrélation de Matthews dans R
Le code suivant montre comment définir un vecteur de classes prédites et un vecteur de classes réelles, puis calculer le coefficient de corrélation de Matthews à l’aide de la fonction mcc() du package mltools :
library(mltools) #define vector of actual classes actual <- rep(c(1, 0), times=c(20, 380)) #define vector of predicted classes preds <- rep(c(1, 0, 1, 0), times=c(15, 5, 5, 375)) #calculate Matthews correlation coefficient mcc(preds, actual) [1] 0.7368421
Le coefficient de corrélation de Matthews est de 0,7368 .
Cela correspond à la valeur que nous avons calculée manuellement plus tôt.
Si vous souhaitez calculer le coefficient de corrélation de Matthews pour une matrice de confusion, vous pouvez utiliser l’argument confusionM comme suit :
library(mltools) #create confusion matrix conf_matrix <- matrix(c(15, 5, 5, 375), nrow=2) #view confusion matrix conf_matrix [,1] [,2] [1,] 15 5 [2,] 5 375 #calculate Matthews correlation coefficient for confusion matrix mcc(confusionM = conf_matrix) [1] 0.7368421
Encore une fois, le coefficient de corrélation de Matthews est de 0,7368.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :
Comment effectuer une régression logistique dans R
Comment tracer une courbe ROC à l’aide de ggplot2
Comment calculer le score F1 dans R
