Coefficient de corrélation de Pearson

Le coefficient de corrélation de Pearson (également connu sous le nom de « coefficient de corrélation produit-moment ») est une mesure de l’association linéaire entre deux variables X et Y. Il a une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

La formule pour trouver le coefficient de corrélation de Pearson

La formule pour trouver le coefficient de corrélation de Pearson, noté r , pour un échantillon de données est ( via Wikipedia ) :

Vous n’aurez probablement jamais à calculer cette formule à la main puisque vous pouvez utiliser un logiciel pour le faire à votre place, mais il est utile de comprendre ce que fait exactement cette formule en parcourant un exemple.

Supposons que nous ayons l’ensemble de données suivant :

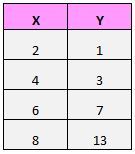
Si nous traçons ces paires (X, Y) sur un nuage de points, cela ressemblerait à ceci :

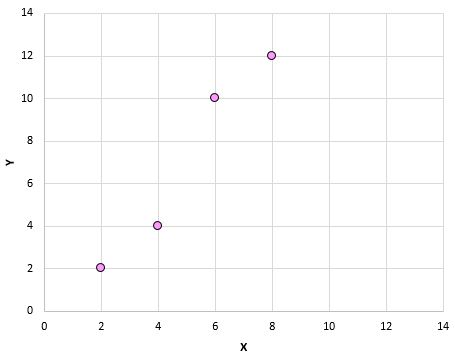
Rien qu’en regardant ce nuage de points, nous pouvons constater qu’il existe une association positive entre les variables X et Y : lorsque X augmente, Y a tendance à augmenter également. Mais pour quantifier exactement dans quelle mesure ces deux variables sont positivement associées, nous devons trouver le coefficient de corrélation de Pearson.

Concentrons-nous uniquement sur le numérateur de la formule :

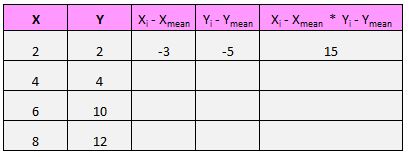
Pour chaque paire (X, Y) de notre ensemble de données, nous devons trouver la différence entre la valeur x et la valeur moyenne de x, la différence entre la valeur y et la valeur moyenne de y, puis multiplier ces deux nombres ensemble.

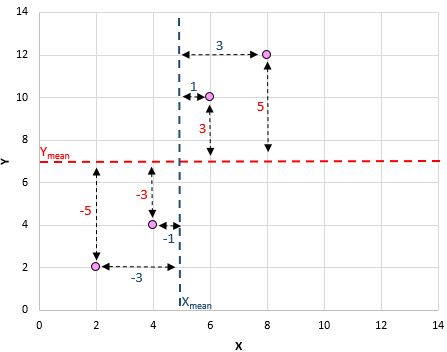
Par exemple, notre première paire (X, Y) est (2, 2). La valeur moyenne de x dans cet ensemble de données est de 5 et la valeur moyenne de y dans cet ensemble de données est de 7. Ainsi, la différence entre la valeur x de cette paire et la valeur moyenne de x est de 2 – 5 = -3. La différence entre la valeur y de cette paire et la valeur y moyenne est de 2 – 7 = -5. Ensuite, lorsque nous multiplions ces deux nombres, nous obtenons -3 * -5 = 15.

Voici un aperçu visuel de ce que nous venons de faire :

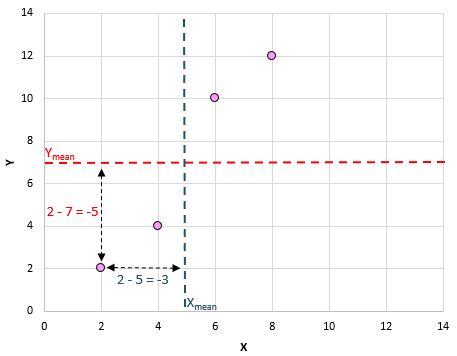
Ensuite, il suffit de faire ceci pour chaque paire :

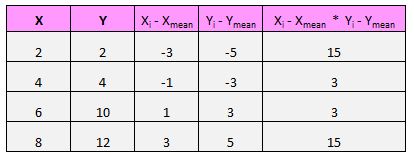
La dernière étape pour obtenir le numérateur de la formule consiste simplement à additionner toutes ces valeurs :

15 + 3 +3 + 15 = 36

Ensuite, le dénominateur de la formule nous dit de trouver la somme de toutes les différences au carré pour x et y, puis de multiplier ces deux nombres ensemble, puis de prendre la racine carrée :

Nous allons donc d’abord trouver la somme des carrés des différences pour x et y :

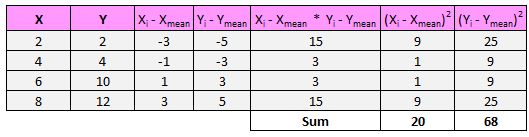
Ensuite, nous multiplierons ces deux nombres ensemble : 20 * 68 = 1 360.

Enfin, nous prendrons la racine carrée : √ 1 360 = 36,88

Nous avons donc trouvé que le numérateur de la formule est 36 et le dénominateur est 36,88. Cela signifie que notre coefficient de corrélation de Pearson est r = 36 / 36,88 = 0,976

Ce nombre est proche de 1, ce qui indique qu’il existe une forte relation linéaire positive entre nos variables X et Y . Cela confirme la relation que nous avons observée dans le nuage de points.

Visualiser les corrélations

Rappelons qu’un coefficient de corrélation de Pearson nous indique le type de relation linéaire (positive, négative, aucune) entre deux variables ainsi que la force de cette relation (faible, modérée, forte).

Lorsque nous créons un nuage de points de deux variables, nous pouvons voir la relation réelle entre deux variables. Voici les nombreux types de relations linéaires que nous pourrions observer :

Relation forte et positive : à mesure que la variable sur l’axe des x augmente, la variable sur l’axe des y augmente également. Les points sont étroitement regroupés, ce qui indique une relation forte.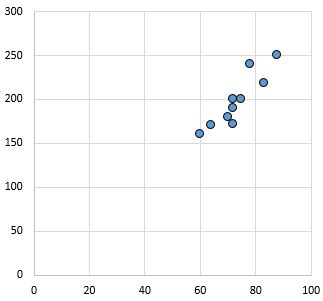

Coefficient de corrélation de Pearson : 0,94

Relation faible et positive : à mesure que la variable sur l’axe des x augmente, la variable sur l’axe des y augmente également. Les points sont assez dispersés, ce qui indique une relation faible.

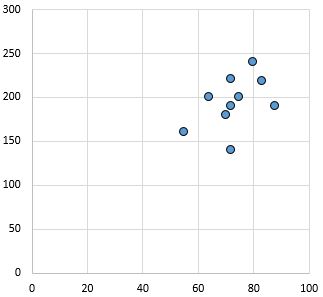
Coefficient de corrélation de Pearson : 0,44

Aucune relation : Il n’existe aucune relation claire (positive ou négative) entre les variables.

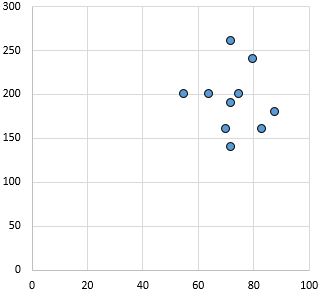
Coefficient de corrélation de Pearson : 0,03

Relation forte et négative : à mesure que la variable sur l’axe des x augmente, la variable sur l’axe des y diminue. Les points sont étroitement serrés les uns contre les autres, ce qui indique une relation forte.

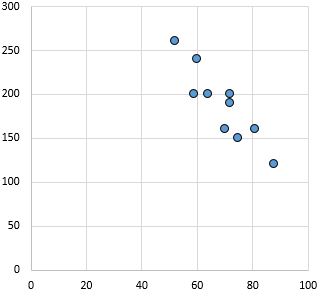
Coefficient de corrélation de Pearson : -0,87

Relation faible et négative : à mesure que la variable sur l’axe des x augmente, la variable sur l’axe des y diminue. Les points sont assez dispersés, ce qui indique une relation faible.

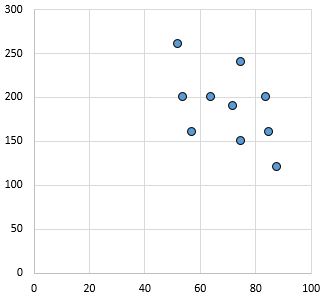
Coefficient de corrélation de Pearson : – 0,46

Test de signification d’un coefficient de corrélation de Pearson

Lorsque nous trouvons le coefficient de corrélation de Pearson pour un ensemble de données, nous travaillons souvent avec un échantillon de données provenant d’une population plus large. Cela signifie qu’il est possible de trouver une corrélation non nulle pour deux variables même si elles ne sont en réalité pas corrélées dans la population globale.

Par exemple, supposons que nous créions un nuage de points pour les variables X et Y pour chaque point de données de la population entière et qu’il ressemble à ceci :

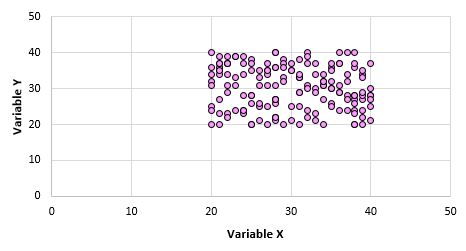
Il est évident que ces deux variables ne sont pas corrélées. Cependant, il est possible que lorsqu’on prend un échantillon de 10 points de la population, on choisisse les points suivants :

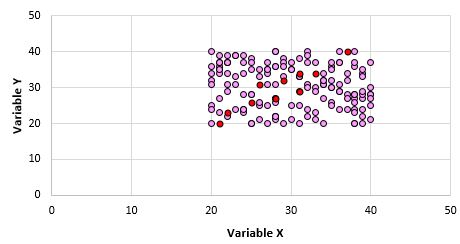
Nous pouvons constater que le coefficient de corrélation de Pearson pour cet échantillon de points est de 0,93, ce qui indique une forte corrélation positive même si la corrélation de population est nulle.

Afin de tester si une corrélation entre deux variables est statistiquement significative ou non, nous pouvons trouver la statistique de test suivante :

Statistique de test T = r * √ (n-2) / (1-r ² )

où n est le nombre de paires dans notre échantillon, r est le coefficient de corrélation de Pearson et la statistique de test T suit une distribution avec n-2 degrés de liberté.

Passons en revue un exemple de la manière de tester la signification d’un coefficient de corrélation de Pearson.

Exemple

L’ensemble de données suivant montre la taille et le poids de 12 individus :

Le nuage de points ci-dessous montre la valeur de ces deux variables :

Le coefficient de corrélation de Pearson pour ces deux variables est r = 0,836.

La statistique de test T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

Selon notre calculateur de distribution t , un score de 4,804 avec 10 degrés de liberté a une valeur p de 0,0007. Puisque 0,0007 < 0,05, nous pouvons conclure que la corrélation entre le poids et la taille dans cet exemple est statistiquement significative à alpha = 0,05.

Précautions

Bien qu’un coefficient de corrélation de Pearson puisse être utile pour nous indiquer si deux variables ont ou non une association linéaire, nous devons garder trois choses à l’esprit lors de l’interprétation d’un coefficient de corrélation de Pearson :

1. La corrélation n’implique pas la causalité. Ce n’est pas parce que deux variables sont corrélées que l’une fait nécessairement apparaître l’autre plus ou moins souvent. Un exemple classique en est la corrélation positive entre les ventes de glaces et les attaques de requins. Lorsque les ventes de glaces augmentent à certaines périodes de l’année, les attaques de requins ont également tendance à augmenter.

Cela signifie-t-il que la consommation de glaces provoque des attaques de requins ? Bien sûr que non! Cela signifie simplement qu’en été, la consommation de glace et les attaques de requins ont tendance à augmenter, car la glace est plus populaire en été et plus de gens vont dans l’océan pendant l’été.

2. Les corrélations sont sensibles aux valeurs aberrantes. Une valeur aberrante extrême peut modifier considérablement un coefficient de corrélation de Pearson. Prenons l’exemple ci-dessous :

Les variables X et Y ont un coefficient de corrélation de Pearson de 0,00 . Mais imaginez que nous ayons une valeur aberrante dans l’ensemble de données :

Or, le coefficient de corrélation de Pearson pour ces deux variables est de 0,878 . Cette seule valeur aberrante change tout. C’est pourquoi, lorsque vous calculez la corrélation pour deux variables, c’est une bonne idée de visualiser les variables à l’aide d’un nuage de points pour vérifier les valeurs aberrantes.

3. Un coefficient de corrélation de Pearson ne capture pas les relations non linéaires entre deux variables. Imaginons que nous ayons deux variables avec la relation suivante :

Le coefficient de corrélation de Pearson pour ces deux variables est de 0,00 car elles n’ont pas de relation linéaire. Cependant, ces deux variables ont une relation non linéaire : les valeurs y sont simplement les valeurs x au carré.

Lorsque vous utilisez le coefficient de corrélation de Pearson, gardez à l’esprit que vous testez simplement si deux variables sont linéairement liées. Même si un coefficient de corrélation de Pearson nous indique que deux variables ne sont pas corrélées, elles pourraient quand même entretenir un certain type de relation non linéaire. C’est une autre raison pour laquelle il est utile de créer un nuage de points lors de l’analyse de la relation entre deux variables : cela peut vous aider à détecter une relation non linéaire.