Coefficient de corrélation intraclasse : définition + exemple
Un coefficient de corrélation intraclasse (ICC) est utilisé pour mesurer la fiabilité des notes dans les études où il y a deux évaluateurs ou plus.
La valeur d’un ICC peut varier de 0 à 1, 0 indiquant une absence de fiabilité parmi les évaluateurs et 1 indiquant une fiabilité parfaite parmi les évaluateurs.
En termes simples, un ICC est utilisé pour déterminer si les éléments (ou sujets) peuvent être évalués de manière fiable par différents évaluateurs.
Il existe plusieurs versions différentes d’un ICC qui peuvent être calculées, en fonction des trois facteurs suivants :
- Modèle : effets aléatoires unidirectionnels, effets aléatoires bidirectionnels ou effets mixtes bidirectionnels
- Type de relation : cohérence ou accord absolu
- Unité : évaluateur unique ou moyenne des évaluateurs
Voici une brève description des trois modèles différents :
1. Modèle à effets aléatoires unidirectionnels : ce modèle suppose que chaque sujet est évalué par un groupe différent d’évaluateurs choisis au hasard. Grâce à ce modèle, les évaluateurs sont considérés comme la source des effets aléatoires. Ce modèle est rarement utilisé en pratique car le même groupe d’évaluateurs est généralement utilisé pour évaluer chaque matière.
2. Modèle à effets aléatoires bidirectionnels : ce modèle suppose qu’un groupe d’évaluateurs k est sélectionné au hasard dans une population, puis utilisé pour évaluer les sujets. En utilisant ce modèle, les évaluateurs et les sujets sont considérés comme des sources d’effets aléatoires. Ce modèle est souvent utilisé lorsque nous souhaitons généraliser nos résultats à des évaluateurs similaires à ceux utilisés dans l’étude.
3. Modèle bidirectionnel à effets mixtes : ce modèle suppose également qu’un groupe d’évaluateurs k est sélectionné au hasard dans une population, puis utilisé pour évaluer les sujets. Cependant, ce modèle suppose que le groupe d’évaluateurs que nous avons choisi est le seul évaluateur intéressant, ce qui signifie que nous ne souhaitons pas généraliser nos résultats à d’autres évaluateurs qui pourraient également partager des caractéristiques similaires à celles des évaluateurs utilisés dans l’étude.
Voici une brève description des deux différents types de relations que nous pourrions vouloir mesurer :
1. Cohérence : nous nous intéressons aux différences systématiques entre les notes des juges (par exemple, les juges ont-ils noté des sujets similaires comme étant faibles et élevés ?)
2. Accord absolu : nous nous intéressons aux différences absolues entre les notes des juges (par exemple, quelle est la différence absolue entre les notes du juge A et du juge B ?)
Voici une brève description des deux unités différentes qui pourraient nous intéresser :
1. Évaluateur unique : nous souhaitons uniquement utiliser les notes d’un seul évaluateur comme base de mesure.
2. Moyenne des évaluateurs : Nous souhaitons utiliser la moyenne des notes de tous les juges comme base de mesure.
Remarque : Si vous souhaitez mesurer le niveau d’accord entre deux évaluateurs qui évaluent chacun des éléments sur un résultat dichotomique , vous devez plutôt utiliser le Kappa de Cohen .
Comment interpréter le coefficient de corrélation intraclasse
Voici comment interpréter la valeur d’un coefficient de corrélation intraclasse, selon Koo & Li :
- Moins de 0,50 : mauvaise fiabilité
- Entre 0,5 et 0,75 : Fiabilité modérée
- Entre 0,75 et 0,9 : Bonne fiabilité
- Supérieur à 0,9 : Excellente fiabilité
L’exemple suivant montre comment calculer un coefficient de corrélation intraclasse en pratique.
Exemple : Calcul du coefficient de corrélation intraclasse
Supposons que quatre juges différents soient invités à évaluer la qualité de 10 examens d’entrée à l’université différents. Les résultats sont montrés plus bas:
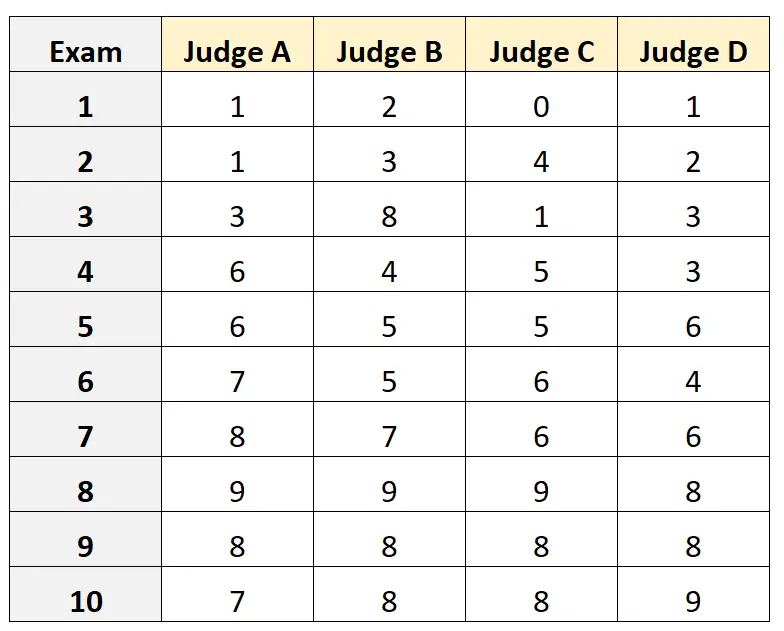
Supposons que les quatre juges aient été sélectionnés au hasard parmi une population de juges qualifiés pour l’examen d’entrée et que nous souhaitions mesurer l’accord absolu entre les juges et que nous souhaitions utiliser les notes du point de vue d’un seul évaluateur comme base de notre mesure.
Nous pouvons utiliser le code suivant dans R pour ajuster un modèle à effets aléatoires bidirectionnel , en utilisant l’accord absolu comme relation entre les évaluateurs et en utilisant l’unité unique comme unité d’intérêt :
#load the interrater reliability package library(irr) #define data data <- data.frame(A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7), B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8), C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8), D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9)) #calculate ICC icc(data, model = "twoway", type = "agreement", unit = "single") Model: twoway Type : agreement Subjects = 10 Raters = 4 ICC(A,1) = 0.782 F-Test, H0: r0 = 0 ; H1: r0 > 0 F(9,30) = 15.3 , p = 5.93e-09 95%-Confidence Interval for ICC Population Values: 0.554 < ICC < 0.931
Le coefficient de corrélation intraclasse (ICC) s’avère être de 0,782 .
Sur la base des règles empiriques d’interprétation de l’ICC, nous conclurions qu’un ICC de 0,782 indique que les examens peuvent être notés avec une « bonne » fiabilité par différents évaluateurs.
Ressources additionnelles
Les didacticiels suivants fournissent des explications détaillées sur la façon de calculer l’ICC dans différents logiciels statistiques :
Comment calculer le coefficient de corrélation intraclasse dans Excel
Comment calculer le coefficient de corrélation intraclasse dans R
Comment calculer le coefficient de corrélation intraclasse en Python
