Comment calculer un coefficient de corrélation sur une calculatrice TI-84
Un coefficient de corrélation est une mesure de l’association linéaire entre deux variables. Il peut prendre une valeur comprise entre -1 et 1 où :
- -1 indique une corrélation linéaire parfaitement négative entre deux variables
- 0 indique aucune corrélation linéaire entre deux variables
- 1 indique une corrélation linéaire parfaitement positive entre deux variables
Vous pouvez utiliser les étapes suivantes pour calculer le coefficient de corrélation entre deux variables sur une calculatrice TI-84 :
Étape 1 : activez les diagnostics.
Tout d’abord, nous devons activer les diagnostics. Pour ce faire, appuyez sur 2ème puis appuyez sur le chiffre 0. Cela nous amènera à l’écran CATALOGUE.

Faites défiler jusqu’à DiagnosticOn et appuyez sur ENTER .
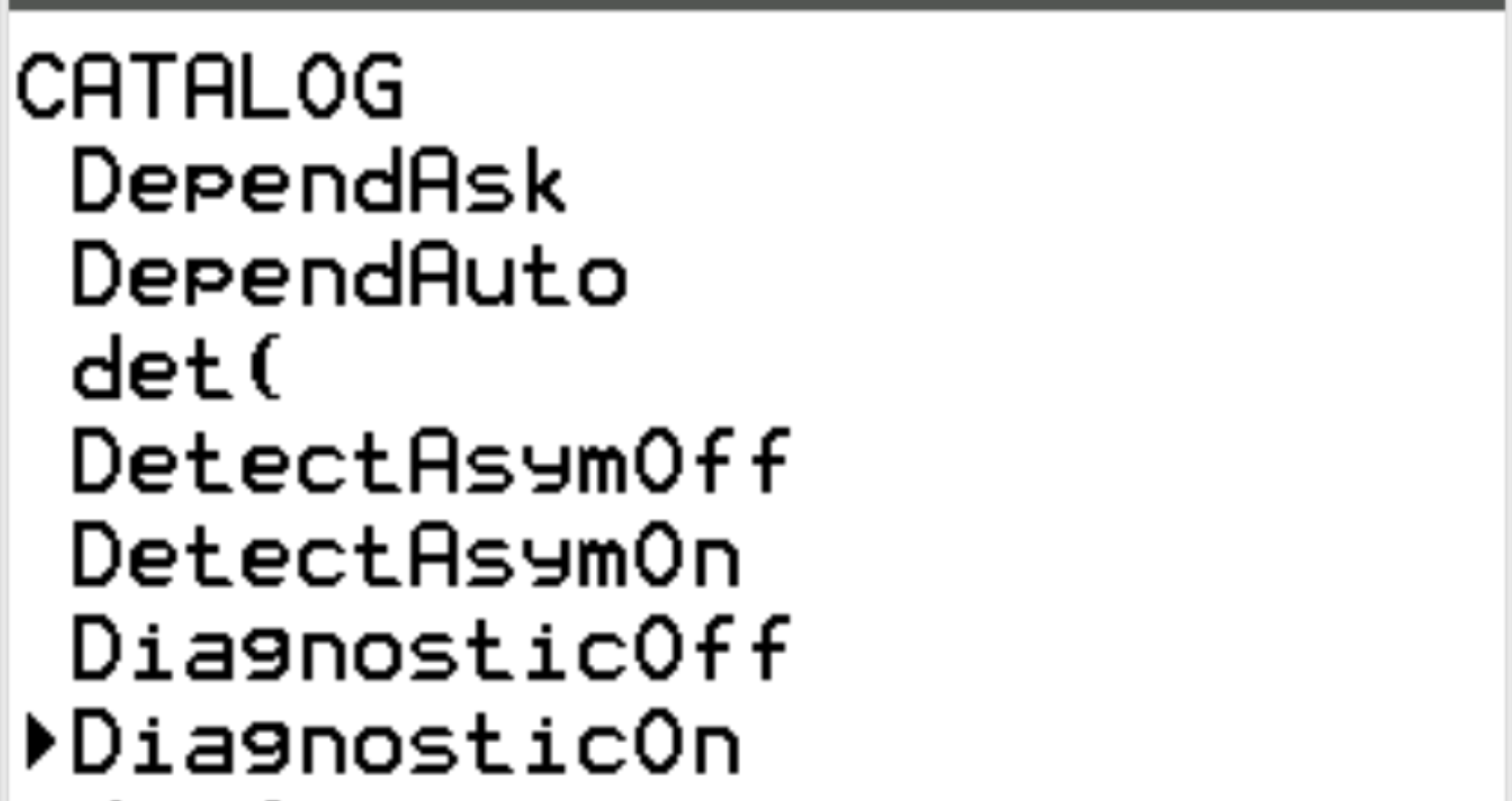
Puis appuyez à nouveau sur ENTER .
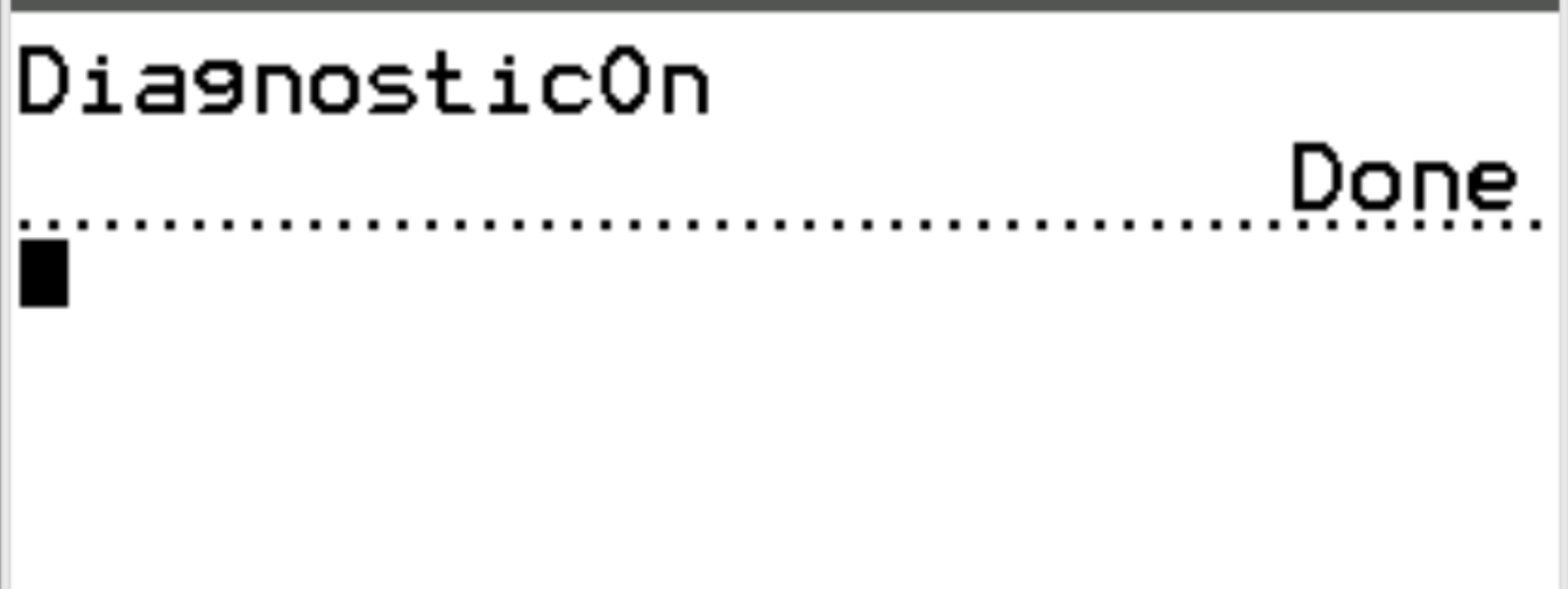
Les diagnostics sont désormais activés afin que nous puissions calculer le coefficient de corrélation entre deux variables.
Étape 2 : Saisissez les données.
Ensuite, nous devons saisir les valeurs des données pour nos deux variables. Appuyez sur Stat puis appuyez sur EDIT . Saisissez les valeurs de la première variable dans la colonne L1 et les valeurs de la deuxième variable dans la colonne L2 :
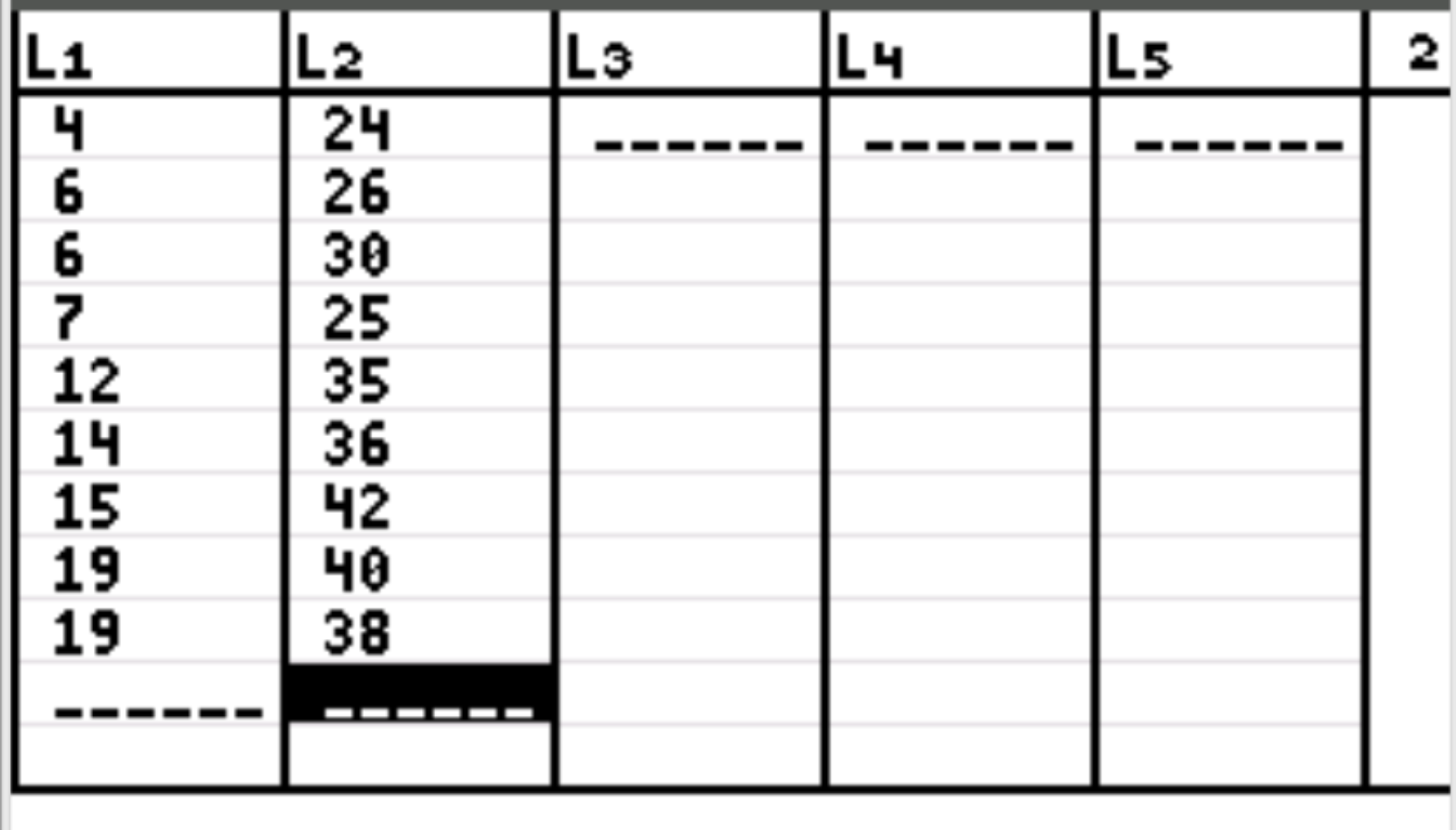
Étape 3 : Trouvez le coefficient de corrélation.
Ensuite, nous calculerons le coefficient de corrélation entre les deux variables. Appuyez sur Stat puis faites défiler jusqu’à CALC . Faites ensuite défiler jusqu’à 8 : Linreg(a+bx) et appuyez sur Enter .
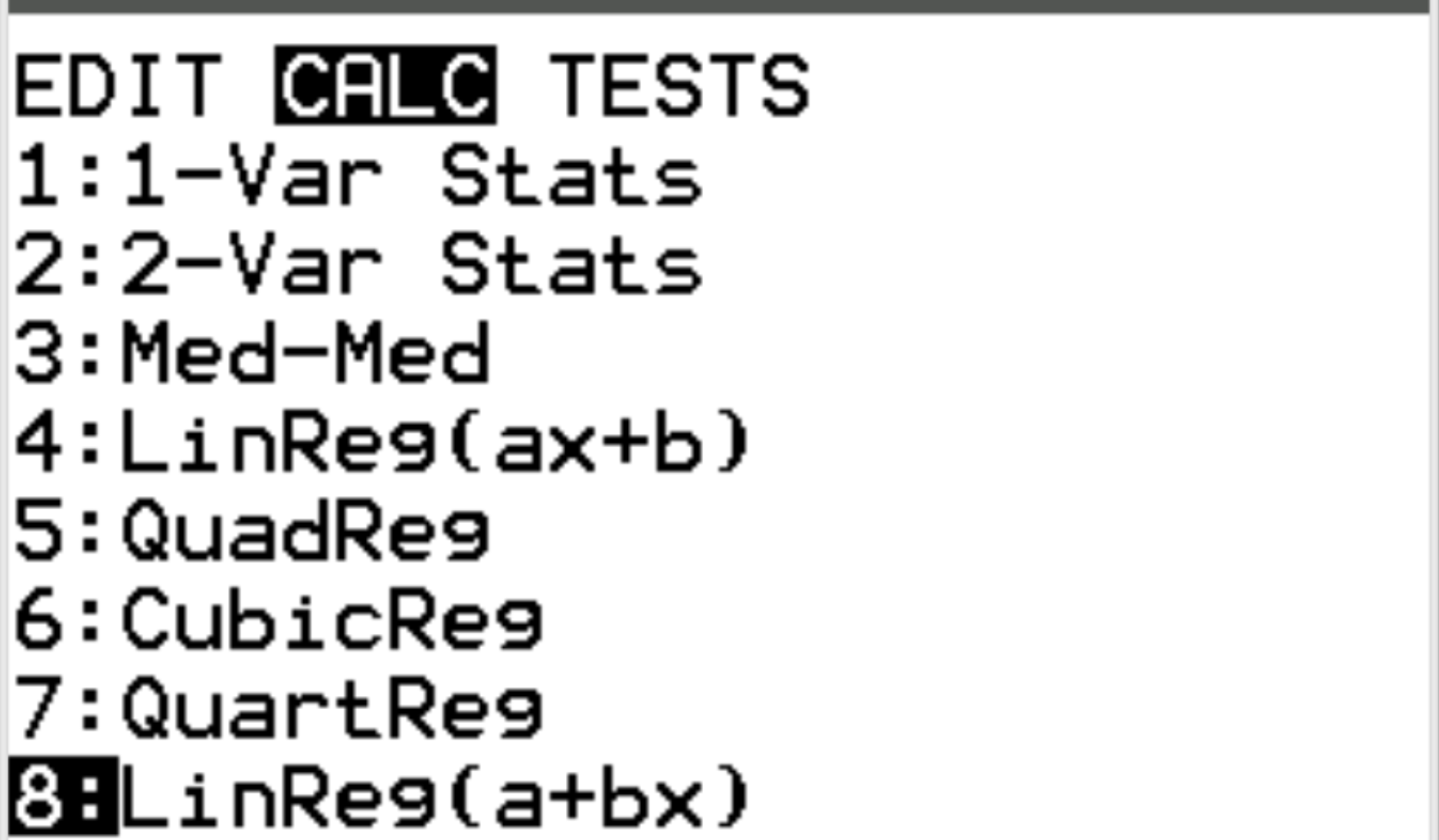
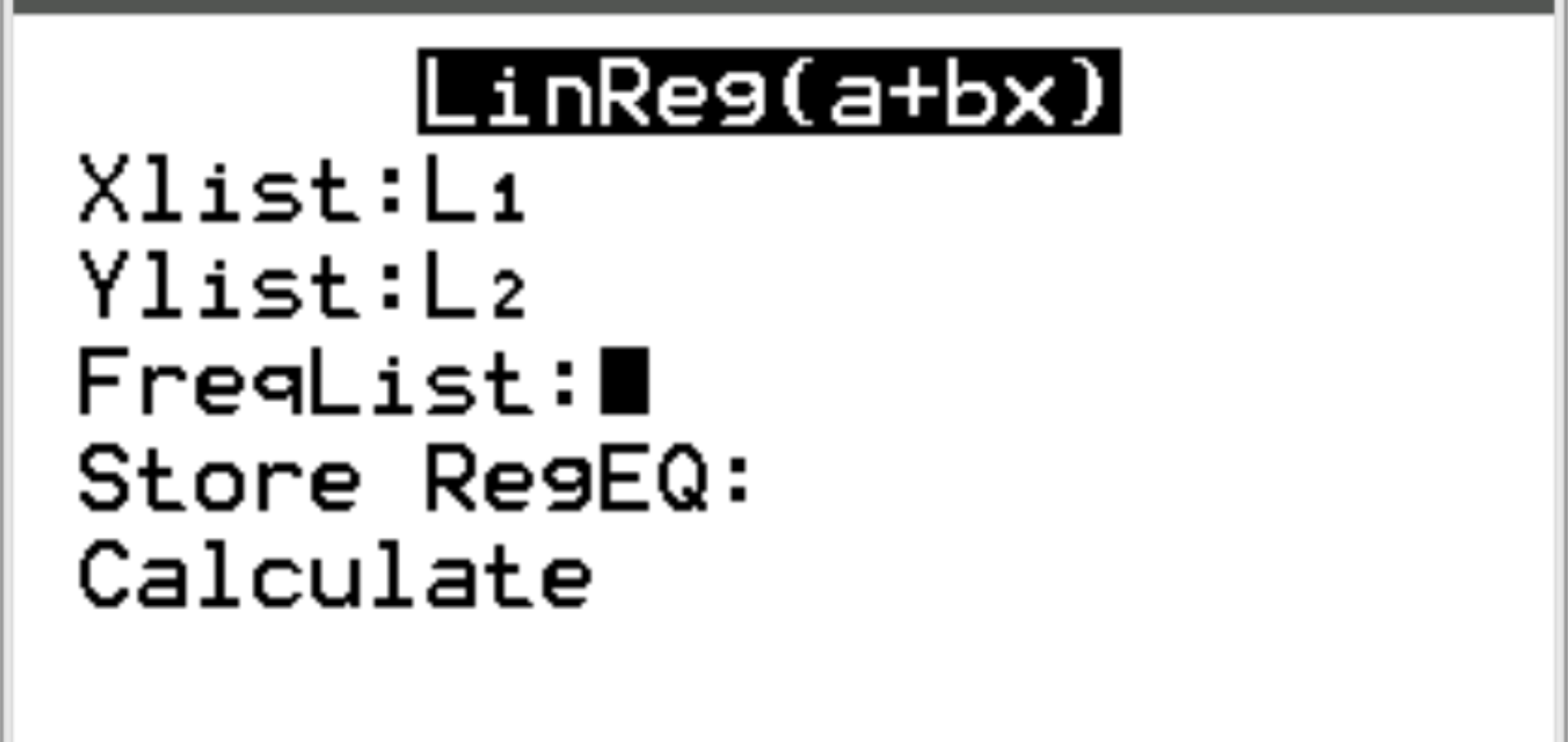
Pour Xlist et Ylist, assurez-vous que L1 et L2 sont sélectionnés car ce sont les colonnes que nous avons utilisées pour saisir nos données. Laissez FreqList vide. Faites défiler jusqu’à Calculer et appuyez sur Entrée .
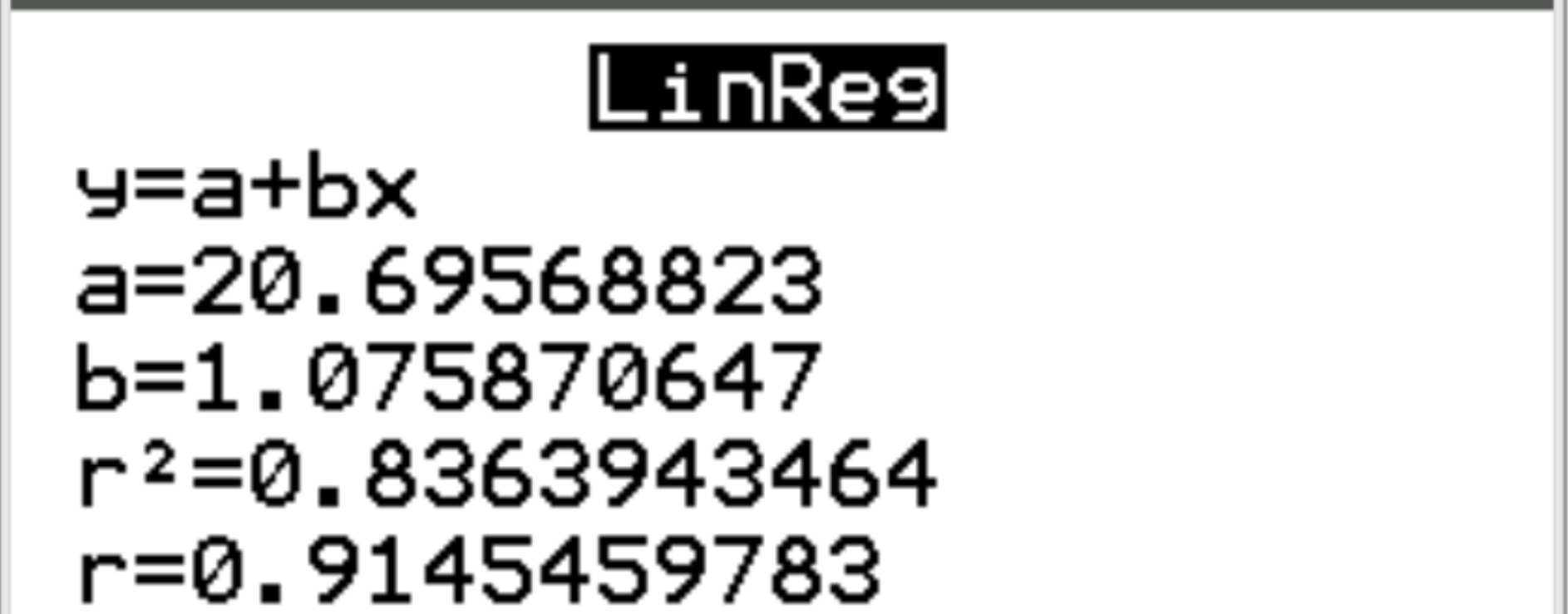
Sur le nouvel écran, nous pouvons voir que le coefficient de corrélation (r) entre les deux variables est de 0,9145 .
Comment interpréter un coefficient de corrélation
Le tableau suivant montre la règle empirique pour interpréter la force de la relation entre deux variables en fonction de la valeur de r :
| Valeur absolue de r | Force de la relation |
|---|---|
| r < 0,25 | Pas de relation |
| 0,25 < r < 0,5 | Faible relation |
| 0,5 < r < 0,75 | Relation modérée |
| r > 0,75 | Relation forte |
Dans notre exemple, un coefficient de corrélation de 0,9145 indique une forte relation positive entre les deux variables.
