Coefficient de détermination (R au carré)

Par Pr Amélia Rodriguez août 2, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est le coefficient de détermination (ou R carré) en statistiques. Ainsi, vous découvrirez comment calculer le coefficient de détermination, comment il est interprété et, en plus, un calculateur en ligne pour calculer le coefficient de détermination d’un échantillon de données.

Quel est le coefficient de détermination (R au carré) ?

Le coefficient de détermination , dont le symbole est R ² ( R au carré ), est une statistique qui mesure la qualité de l’ajustement d’un modèle de régression. Le coefficient de détermination montre dans quelle mesure un modèle de régression s’adapte à un ensemble de données, c’est-à-dire qu’il indique le pourcentage expliqué par le modèle de régression.

Par conséquent, plus le coefficient de détermination est élevé, meilleur est le modèle de régression. Bien que cette condition ne soit pas toujours remplie, on s’intéresse en principe à un coefficient de détermination aussi grand que possible. Nous verrons ci-dessous comment interpréter le coefficient de détermination.

Formule du coefficient de détermination

Le coefficient de détermination est égal à un moins le rapport entre la variance résiduelle et la variance de la variable dépendante. Le coefficient de détermination peut également être calculé en soustrayant un moins la somme des carrés des résidus sur la somme totale des carrés.

Ainsi, la formule pour calculer le coefficient de détermination est la suivante :

formule du coefficient de détermination, formule du r carré

Où:

$R^2$ est le coefficient de détermination.
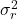$\sigma_r^2$ est la variance résiduelle.
$\sigma^2$ est la variance de la variable dépendante Y.
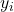$y_{i}$ est la valeur de la variable dépendante d’observation i.
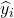$\widehat{y}_{i}$ est la valeur approximée par le modèle de régression pour l’observation i.
$\overline{y}$ est la moyenne de la variable dépendante de toutes les observations.

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer le coefficient de détermination pour n’importe quel ensemble de données.

Pour le cas du modèle de régression linéaire, le coefficient de détermination est équivalent au carré du coefficient de corrélation :

$R^2=\cfrac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2$

Où

$\sigma_{XY}^2$ est la covariance des variables X et Y, $\sigma_X^2$ et $\sigma_Y^2$ sont les variances de la variable indépendante X et de la variable dépendante Y respectivement.

Calculateur de coefficient de détermination

Branchez un échantillon de données dans la calculatrice ci-dessous pour ajuster un modèle de régression linéaire simple et calculer son coefficient de détermination. Vous devez séparer les paires de données, de sorte que dans la première case il n’y ait que les valeurs de la variable indépendante X et dans la deuxième case il n’y ait que les valeurs de la variable dépendante Y.

Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Interprétation du coefficient de détermination

Dans cette section, nous verrons comment interpréter le coefficient de détermination, car il est inutile de connaître la valeur du coefficient de détermination si l’on ne sait pas ce que cela signifie plus tard.

La valeur du coefficient de détermination peut aller de 0 à 1, cependant, elle est généralement exprimée en pourcentage, donc le minimum est de 0 % et le maximum est de 100 %.

Concernant l’ interprétation du coefficient de détermination , plus sa valeur est élevée signifie que le modèle de régression explique mieux l’échantillon de données. Ainsi, plus le coefficient de détermination est proche de 1, plus le modèle sera ajusté. En revanche, plus il est proche de 0, moins le modèle de régression réalisé sera fiable.

Cependant, lorsque l’on compare deux modèles de régression, le modèle avec un coefficient de régression plus élevé n’est pas toujours meilleur. Par exemple, un modèle de régression peut avoir un coefficient de régression R ² = 100 % car de nombreuses variables explicatives ont été ajoutées au modèle et, par conséquent, il peut parfaitement expliquer toutes les observations. Mais ce modèle fait sûrement une très mauvaise prédiction pour une nouvelle valeur qui n’a pas été utilisée pour construire le modèle de régression.

Il faut également garder à l’esprit que le modèle de régression obtenu répond aux hypothèses précédentes. Ainsi, un modèle avec un coefficient de détermination très élevé est inutile si la variabilité de ses résidus n’est pas constante (homoscédasticité).

De plus, le coefficient de détermination présente une limite importante, puisqu’il ne pénalise pas l’inclusion de variables explicatives. Logiquement, plus un modèle de régression comporte de variables explicatives, plus le modèle sera complexe, mais mieux il expliquera les données observées et, par conséquent, plus le coefficient de détermination est élevé. Cependant, le coefficient de détermination ajusté prend en compte le nombre de variables du modèle (nous verrons comment il est calculé ci-dessous).

En conclusion, le coefficient de détermination est très utile pour analyser un modèle de régression, car il nous permet de savoir dans quelle mesure le modèle de régression s’est bien ajusté à l’ensemble de données. Cependant, d’autres outils devraient également être utilisés pour revoir le modèle obtenu, comme les graphiques statistiques .

Coefficient de détermination ajusté

Le coefficient de détermination ajusté , également appelé coefficient de détermination corrigé , mesure la qualité de l’ajustement d’un modèle de régression en tenant compte du nombre de variables explicatives incluses dans le modèle.

La différence entre le coefficient de détermination et le coefficient de détermination ajusté est que le coefficient de détermination mesure la qualité de l’ajustement sans prendre en compte le nombre de variables, par contre, le coefficient de détermination ajusté mesure la qualité de l’ajustement pénalisant pour chaque variable ajoutée.

La formule pour calculer le coefficient de détermination ajusté est la suivante :

$\bar{R}^2=1-\cfrac{N-1}{N-k-1}\cdot (1-R^2)$

Où:

$\bar{R}^2$ est le coefficient de détermination ajusté.
$R^2$ est le coefficient de détermination.
$N$ est la taille de l’échantillon.
$k$ est le nombre de variables explicatives dans le modèle de régression.

Par conséquent, le coefficient de détermination ajusté est meilleur que le coefficient de détermination pour comparer deux modèles différents, puisque les modèles peuvent avoir un nombre différent de variables explicatives.

➤ Voir : Coefficient de détermination ajusté

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus