Comment trouver le coefficient de variation sur une calculatrice TI-84

Un coefficient de variation , souvent abrégé en CV , est un moyen de mesurer l’étalement des valeurs dans un ensemble de données par rapport à la moyenne. Il est calculé comme suit :

CV = σ / μ

où:

• σ : l’écart type de l’ensemble de données
• μ : la moyenne de l’ensemble de données

En termes simples, le coefficient de variation est le rapport entre l’écart type et la moyenne.

Il est souvent utilisé pour comparer la variation entre deux ensembles de données différents. Par exemple, en finance, il est utilisé pour comparer le rendement moyen attendu d’un investissement par rapport à l’écart type attendu de l’investissement.

Par exemple, supposons qu’un investisseur envisage d’investir dans les deux fonds communs de placement suivants :

Fonds commun de placement A : moyenne = 9 %, écart-type = 12,4 %

OPCVM B : moyenne = 5 %, écart-type = 8,2 %

L’investisseur peut calculer le coefficient de variation pour chaque fonds :

• CV pour le fonds commun de placement A = 12,4 % / 9 % = 1,38
• CV pour le fonds commun de placement B = 8,2 % / 5 % = 1,64

Étant donné que le fonds commun de placement A a un coefficient de variation plus faible, il offre un meilleur rendement moyen par rapport à l’écart type.

L’exemple suivant, étape par étape, explique comment calculer le coefficient de variation pour l’ensemble de données suivant sur une calculatrice TI-84 :

Ensemble de données : 3, 8, 8, 13, 16, 11

Étape 1 : Saisissez les données

Tout d’abord, nous entrerons les valeurs des données.

Appuyez sur Stat , puis appuyez sur EDIT . Saisissez ensuite les valeurs du jeu de données dans la colonne L1 :

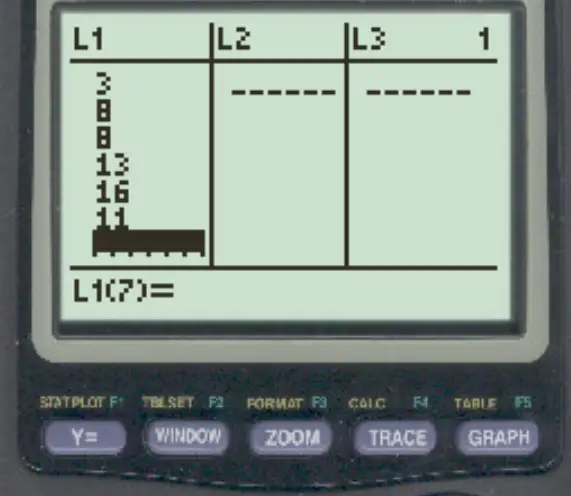
Étape 2 : Trouver le coefficient de variation

Ensuite, appuyez sur Stat , puis faites défiler vers la droite et appuyez sur CALC .

Appuyez ensuite sur 1-Var Stats .

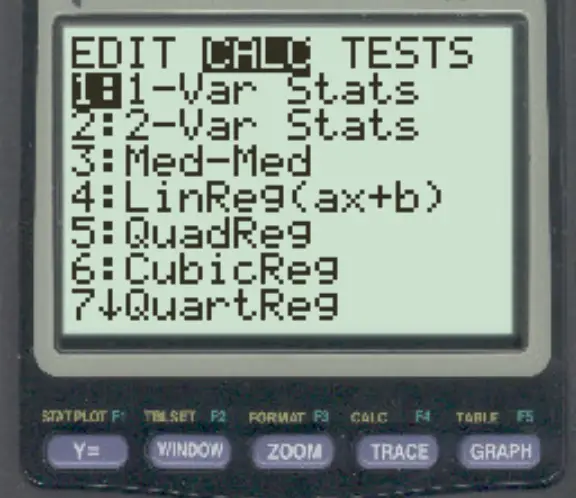
Dans le nouvel écran qui apparaît, appuyez sur Entrée .

Une fois que vous appuyez sur Entrée , une liste de statistiques récapitulatives apparaîtra :

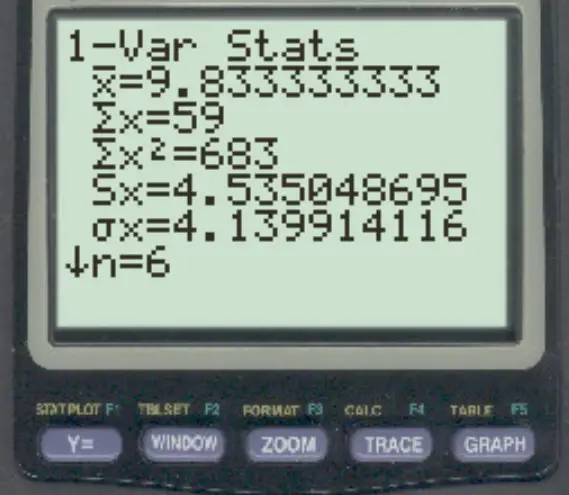
À partir de cet écran, nous pouvons observer les valeurs de la moyenne et de l’écart type de l’échantillon :

• Moyenne ( x ) : 9,8333
• Écart type de l’échantillon (Sx) : 4,535

On peut alors calculer le coefficient de variation comme suit :

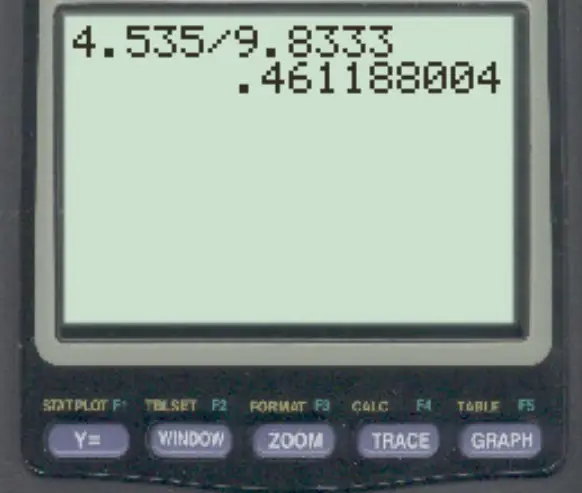
Le coefficient de variation pour cet ensemble de données s’avère être de 0,4611 . En pourcentage, cela équivaut à 46,11 % .

Ressources additionnelles

Comment trouver un résumé de cinq chiffres sur une calculatrice TI-84
Comment trouver l’intervalle interquartile sur une calculatrice TI-84