Comment calculer le d de Cohen dans Excel

En statistiques, lorsque nous souhaitons déterminer s’il existe ou non une différence significative entre deux groupes, nous effectuons souvent un test d’hypothèse, qui aboutit à une valeur p .

Si cette valeur p est inférieure à un certain niveau de signification (les choix courants sont 0,10, 0,05 et 0,01), nous concluons qu’il existe une différence statistiquement significative entre les deux groupes.

Cependant, même si une valeur p peut nous indiquer s’il existe ou non une différence statistiquement significative entre deux groupes, une taille d’effet peut nous indiquer l’ampleur réelle de cette différence.

L’une des mesures les plus courantes de la taille de l’effet est le d de Cohen , qui est calculé comme suit :

Cohen’s d = ( x ₁ – x ₂ ) / SD groupé

où:

• x ₁ = moyenne du groupe 1
• x ₂ = moyenne du groupe 2
• SD groupé = √ (s ₁ ² + s ₂ ² ) / 2

Ce tutoriel explique comment calculer le d de Cohen dans Excel.

Exemple : le d de Cohen dans Excel

Effectuez les étapes suivantes pour calculer le d de Cohen dans Excel.

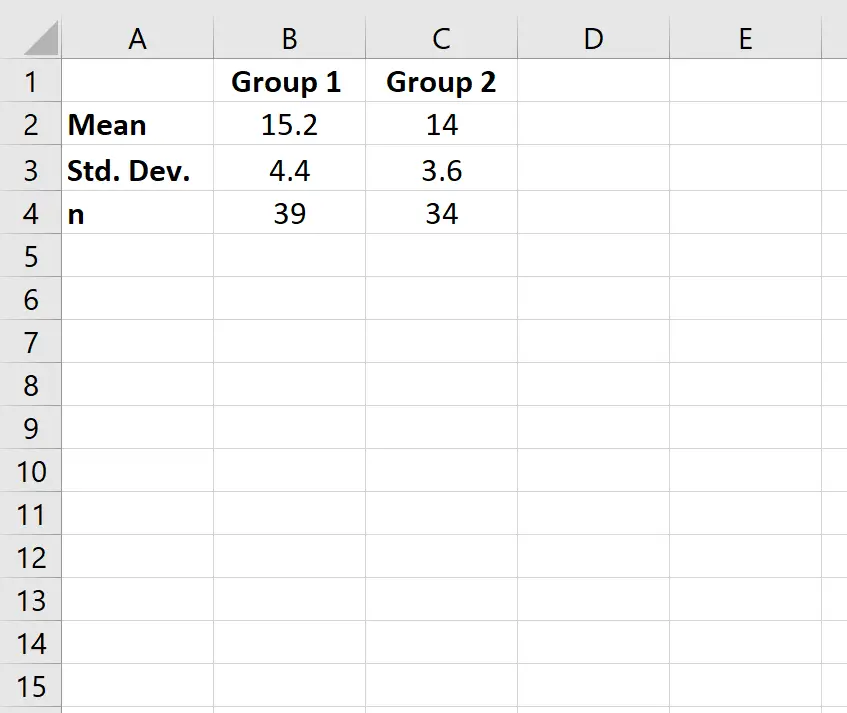
Étape 1 : Saisissez les données.

Tout d’abord, nous entrerons les valeurs de la moyenne, de l’écart type et de la taille de l’échantillon (n) pour deux groupes.

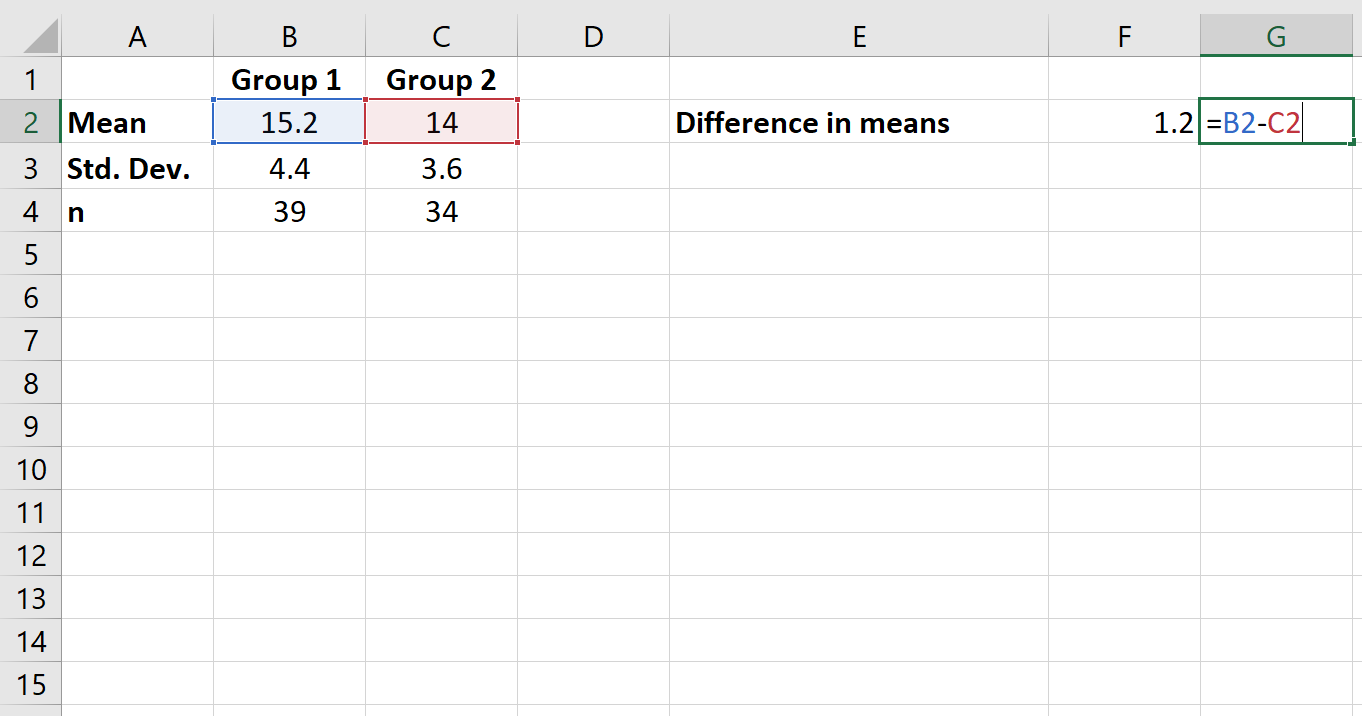
Étape 2 : Calculez la différence de moyenne.

Ensuite, nous calculerons la différence entre les moyennes des groupes.

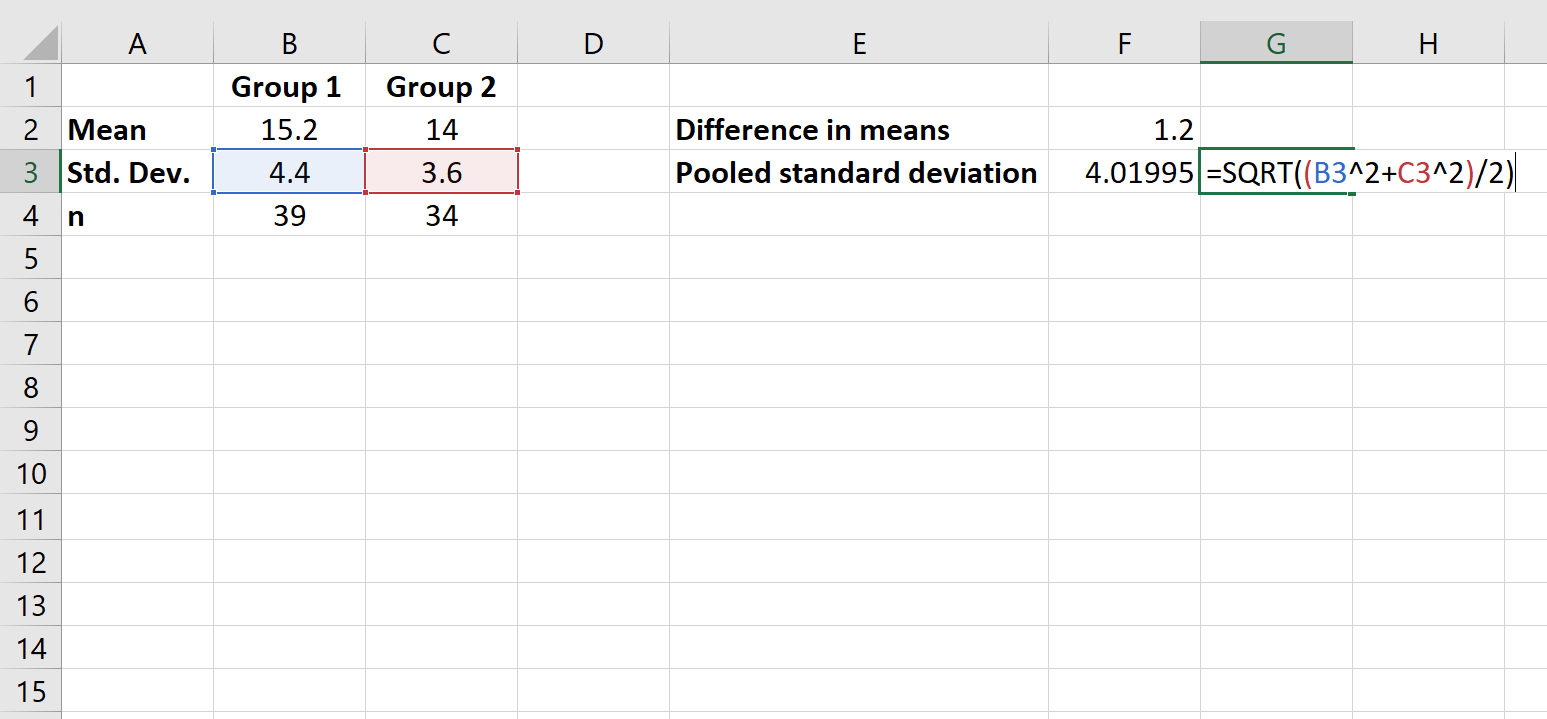
Étape 3 : Calculez l’écart type regroupé.

Ensuite, nous calculerons l’écart type groupé.

Étape 4 : Calculez le d de Cohen.

Enfin, nous calculerons le d de Cohen.

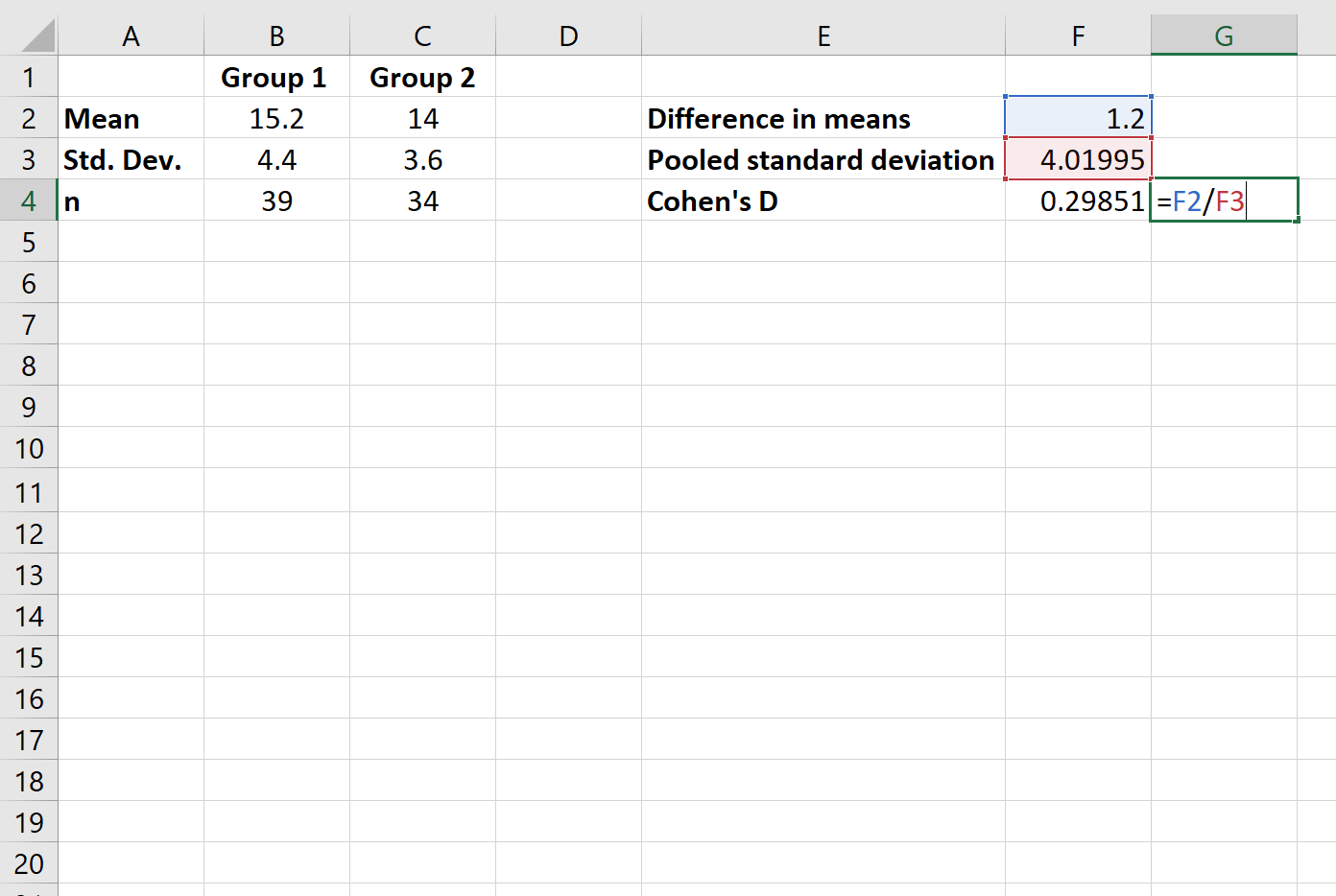
Le d de Cohen s’avère être 0,29851 pour cet exemple.

Comment interpréter le d de Cohen

En règle générale, voici comment interpréter le d de Cohen :

• 0,2 = Petite taille d’effet
• 0,5 = taille d’effet moyenne
• 0,8 = Grande taille d’effet

Dans notre exemple, une taille d’effet de 0,29851 serait probablement considérée comme une taille d’effet faible.

Cela signifie que même si la différence entre les moyennes des deux groupes est statistiquement significativement différente, la différence réelle entre les moyennes des groupes est insignifiante.