Événements collectivement exhaustifs : définition & Exemple

Un ensemble d’événements est collectivement exhaustif si au moins un des événements doit se produire.

Par exemple, si nous lançons un dé alors il doit atterrir sur l’une des valeurs suivantes :

• 1
• 2
• 3
• 4
• 5
• 6

Ainsi, nous dirions que l’ensemble des événements {1, 2, 3, 4, 5, 6} est collectivement exhaustif car le dé doit atterrir sur l’une de ces valeurs.

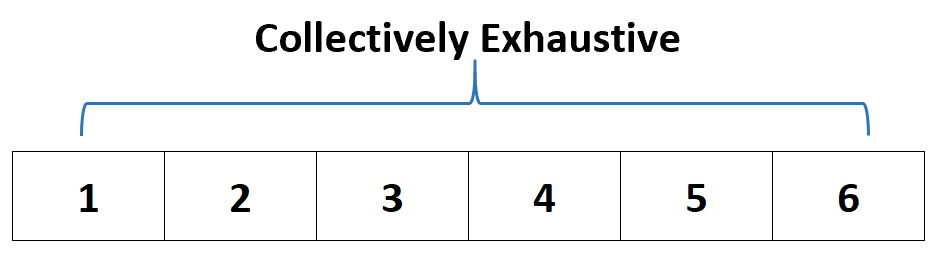
En d’autres termes, cet ensemble d’événements, en tant que collection , épuise toutes les issues possibles.

Les exemples suivants montrent d’autres situations qui illustrent des événements collectivement exhaustifs :

Exemple 1 : lancer une pièce

Supposons que nous lancions une pièce de monnaie une fois. On sait que la pièce doit atterrir sur l’une des valeurs suivantes :

• Têtes
• Queues

Ainsi, l’ensemble des événements {Tête, Face} serait collectivement exhaustif.

Exemple 2 : Faire tourner une toupie

Supposons que nous ayons une roulette qui a trois couleurs différentes : rouge, bleu et vert.

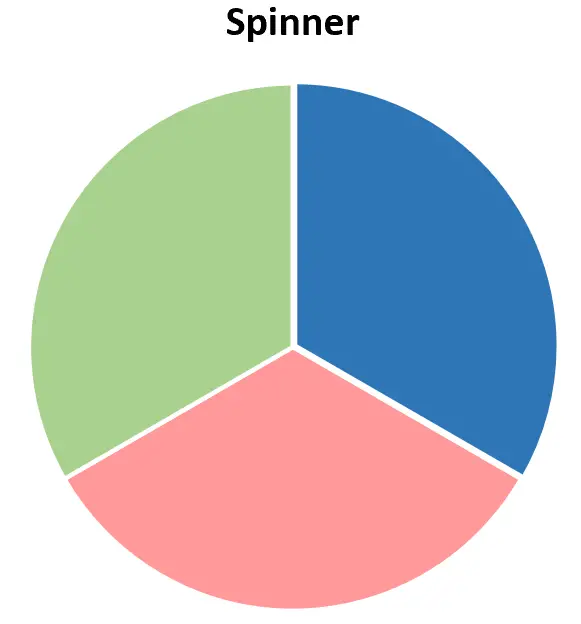
Si nous le faisons tourner une fois alors il doit atterrir sur l’une des valeurs suivantes :

• Rouge
• Bleu
• Vert

Ainsi, l’ensemble des événements {Rouge, Bleu, Vert} serait collectivement exhaustif.

Cependant, l’ensemble des événements {Rouge, Vert} ne serait pas collectivement exhaustif car il ne contient pas tous les résultats possibles.

Exemple 3 : Types de joueurs de basket-ball

Supposons que nous ayons une enquête qui demande aux individus de sélectionner leur poste de basketteur préféré. Les seules réponses possibles sont :

• Meneur de jeu
• Garde de tir
• Petit attaquant
• Puissance en avant
• Centre

Ainsi, l’ensemble des événements {Point Guard, Shooting Guard, Small Forward, Power Forward, Center} serait collectivement exhaustif.

Cependant, l’ensemble des événements {Point Guard, Shooting Guard, Small Forward} ne serait pas collectivement exhaustif car il ne contient pas tous les résultats possibles.

L’importance des événements collectivement exhaustifs dans les enquêtes

Lors de la conception d’enquêtes, il est particulièrement important que les réponses aux questions soient collectivement exhaustives.

Par exemple, supposons qu’une enquête pose la question suivante :

Quel est votre poste de basketteur préféré ?

Et supposons que les réponses potentielles soient :

• Meneur de jeu
• Garde de tir
• Petit attaquant
• Puissance en avant

La position Centre ayant été laissée de côté, ces réponses ne sont pas collectivement exhaustives.

Cela signifie que quelqu’un qui préfère Centre comme position préférée devra choisir l’une des autres options, ce qui signifie que les réponses à l’enquête ne refléteront pas les véritables opinions des personnes interrogées.

Collectivement exhaustif ou mutuellement exclusif

Les événements s’excluent mutuellement s’ils ne peuvent pas se produire en même temps.

Par exemple, laissez l’événement A être l’événement où un dé atterrit sur un nombre pair et laissez l’événement B être l’événement où un dé atterrit sur un nombre impair.

Nous définirions l’ espace échantillon pour les événements comme suit :

• UNE = {2, 4, 6}
• B = {1, 3, 5}

Notez qu’il n’y a pas de chevauchement entre les deux espaces échantillonnés, ce qui signifie qu’ils s’excluent mutuellement. Ils se trouvent également être collectivement exhaustifs car combinés, ils sont capables de rendre compte de tous les résultats potentiels du jet de dé.

Cependant, supposons que nous définissions l’événement A et l’événement B comme suit :

• UNE = {1, 2, 3, 4}
• B = {3, 4, 5, 6}

Dans ce cas, il existe un certain chevauchement entre A et B, ils ne s’excluent donc pas mutuellement. Cependant, combinés, ils sont toujours capables de prendre en compte tous les résultats potentiels du jet de dé.

Cela illustre un point important : un ensemble d’événements peut être collectivement exhaustif sans s’exclure mutuellement .