Comment calculer manuellement une valeur P à partir d’un test T

L’un des tests les plus couramment utilisés en statistique est le test t , qui est souvent utilisé pour déterminer si la moyenne d’une population est égale à une certaine valeur.

Par exemple, supposons que nous voulions savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces. Pour tester cela, nous pourrions collecter un échantillon aléatoire de 20 plantes, trouver la moyenne de l’échantillon et l’écart type de l’échantillon, et effectuer un test t pour déterminer si la hauteur moyenne est réellement égale à 15 pouces.

Les hypothèses nulle et alternative du test sont les suivantes :

H ₀ : µ = 15

H _a : µ ≠ 15

La formule de la statistique de test est :

t = ( X -μ) / (s/√ n )

où x est la moyenne de l’échantillon, μ est la moyenne hypothétique (dans notre exemple, elle serait de 15), s est l’écart type de l’échantillon et n est la taille de l’échantillon.

Une fois que nous connaissons la valeur de t , nous pouvons utiliser un logiciel statistique ou une calculatrice en ligne pour trouver la valeur p correspondante. Si la valeur p est inférieure à un certain niveau alpha (les choix courants sont 0,01, 0,05 et 0,10), nous pouvons alors rejeter l’hypothèse nulle et conclure que la hauteur moyenne des plantes n’est pas égale à 15 pouces.

Cependant, il est également possible d’estimer manuellement la valeur p du test à l’aide d’un tableau de distribution t . Dans cet article, nous expliquerons comment procéder.

Exemple : Calcul manuel de la valeur p à partir d’un test t

Problème : Bob veut savoir si la hauteur moyenne d’une certaine espèce de plante est égale à 15 pouces. Pour tester cela, il collecte un échantillon aléatoire de 20 plantes et constate que la moyenne de l’échantillon est de 14 pouces et que l’écart type de l’échantillon est de 3 pouces. Effectuez un test t en utilisant un niveau alpha de 0,05 pour déterminer si la véritable taille moyenne de la population est réellement de 15 pouces.

Solution:

Étape 1 : Énoncer les hypothèses nulles et alternatives.

H ₀ : µ = 15

H _a : µ ≠ 15

Étape 2 : Trouvez la statistique du test.

t = ( x -μ) / (s/√ n ) = (14-15) / (3/√ 20 ) = -1,49

Étape 3 : Trouvez la valeur p pour la statistique de test.

Pour trouver manuellement la valeur p, nous devons utiliser la table de distribution t avec n-1 degrés de liberté. Dans notre exemple, la taille de notre échantillon est n = 20, donc n-1 = 19.

Dans le tableau de distribution t ci-dessous, nous devons regarder la ligne qui correspond à « 19 » sur le côté gauche et tenter de rechercher la valeur absolue de notre statistique de test 1,49 .

Notez que 1,49 n’apparaît pas dans le tableau, mais il se situe entre les deux valeurs 1,328 et 1,729 .

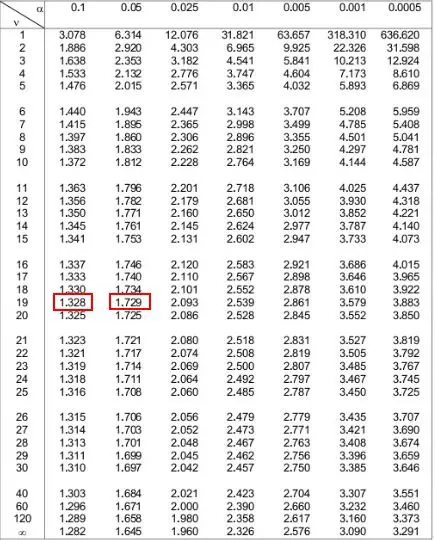
Ensuite, nous pouvons regarder les deux niveaux alpha en haut du tableau qui correspondent à ces deux nombres. On voit qu’ils sont 0,1 et 0,05 .

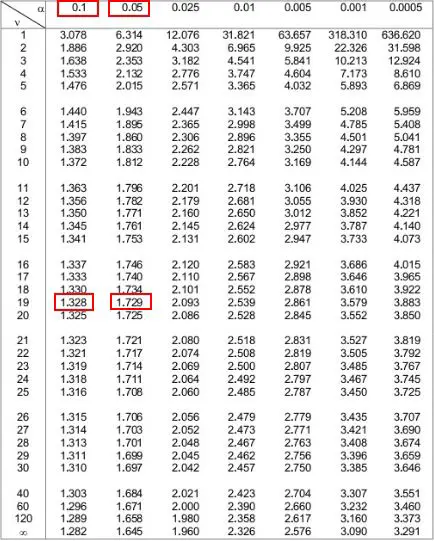
Cela signifie que la valeur p pour un test unilatéral est comprise entre 0,1 et 0,05. Appelons-le .075. Puisque notre test t est bilatéral, nous devons multiplier cette valeur par 2. Ainsi, notre valeur p estimée est 0,075 * 2 = 0,15 .

Étape 4 : Tirez une conclusion.

Étant donné que cette valeur p n’est pas inférieure au niveau alpha choisi de 0,05, nous ne pouvons pas rejeter l’hypothèse nulle. Ainsi, nous n’avons pas suffisamment de preuves pour affirmer que la véritable hauteur moyenne de cette espèce de plante est différente de 15 pouces.

Vérifier les résultats avec une calculatrice

Nous pouvons brancher notre statistique de test t et nos degrés de liberté dans un calculateur de valeur p en ligne pour voir à quel point notre valeur p estimée était proche de la vraie valeur p :

La vraie valeur p est de 0,15264 , ce qui est assez proche de notre valeur p estimée de 0,15 .

Conclusion

Nous avons vu dans cet article qu’il est possible d’estimer manuellement la valeur p d’un test t à l’aide de la table de distribution t. Cependant, dans la plupart des scénarios, vous n’aurez jamais à calculer la valeur p à la main et vous pouvez utiliser soit un logiciel statistique comme R et Excel, soit une calculatrice en ligne pour trouver la valeur p exacte du test.

Dans la plupart des cas, en particulier dans le cadre d’études et d’expériences statistiques rigoureuses, vous souhaiterez utiliser une calculatrice pour trouver la valeur p exacte à partir d’un test t afin d’être aussi précis que possible, mais il est bon de savoir que vous pouvez toujours estimez manuellement la valeur p à partir d’un test t si vous en avez absolument besoin.