Comment effectuer un test Mann-Whitney U dans Excel
Un test U de Mann-Whitney (parfois appelé test de somme de rangs de Wilcoxon) est utilisé pour comparer les différences entre deux échantillons lorsque les distributions d’échantillons ne sont pas normalement distribuées et que les tailles d’échantillon sont petites (n <30).
Il est considéré comme l’équivalent non paramétrique du test t à deux échantillons .
Ce tutoriel explique comment effectuer un test Mann-Whitney U dans Excel.
Exemple : test U de Mann-Whitney dans Excel
Les chercheurs veulent savoir si un traitement du carburant entraîne une modification du mpg moyen d’une voiture. Pour tester cela, ils mènent une expérience dans laquelle ils mesurent le mpg de 12 voitures avec traitement de carburant et de 12 voitures sans traitement.
Étant donné que la taille des échantillons est petite et qu’ils soupçonnent que les distributions des échantillons ne sont pas normalement distribuées, ils ont décidé d’effectuer un test U de Mann-Whitney pour déterminer s’il existe une différence statistiquement significative en mpg entre les deux groupes.
Effectuez les étapes suivantes pour effectuer un test Mann-Whitney U dans Excel.
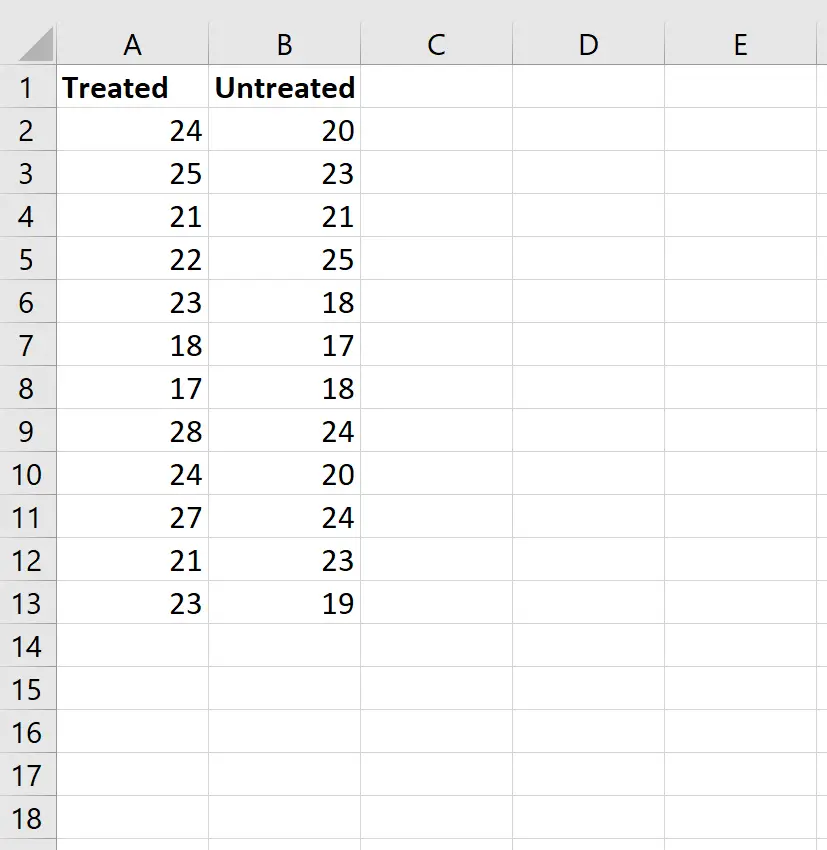
Étape 1 : Saisissez les données.
Saisissez les données comme suit :
Étape 2 : Calculez les classements pour les deux groupes.
Ensuite, nous calculerons les classements pour chaque groupe. L’image suivante montre la formule à utiliser pour calculer le rang de la première valeur du groupe Traité :
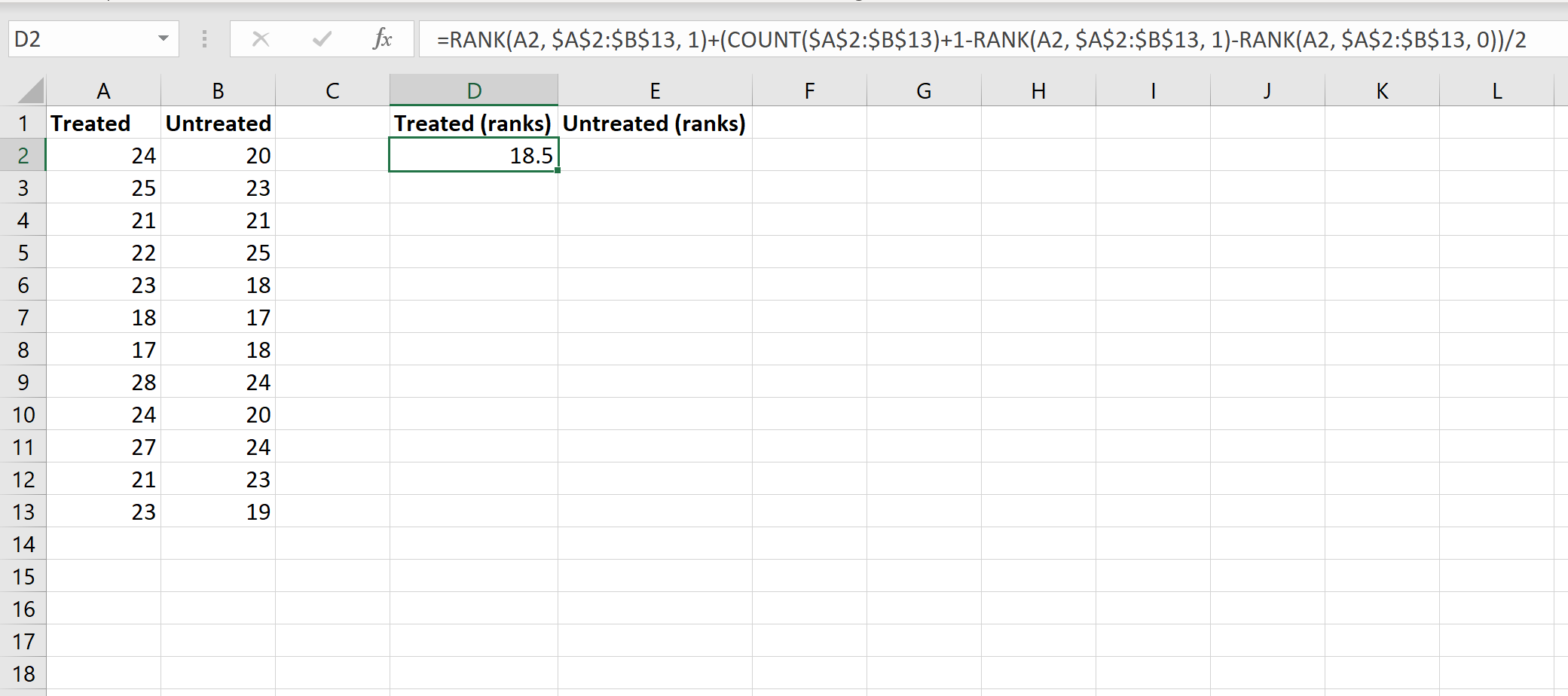
Bien que cette formule soit assez compliquée, vous ne devez la saisir qu’une seule fois. Ensuite, vous pouvez simplement faire glisser la formule vers toutes les autres cellules pour remplir les rangs :
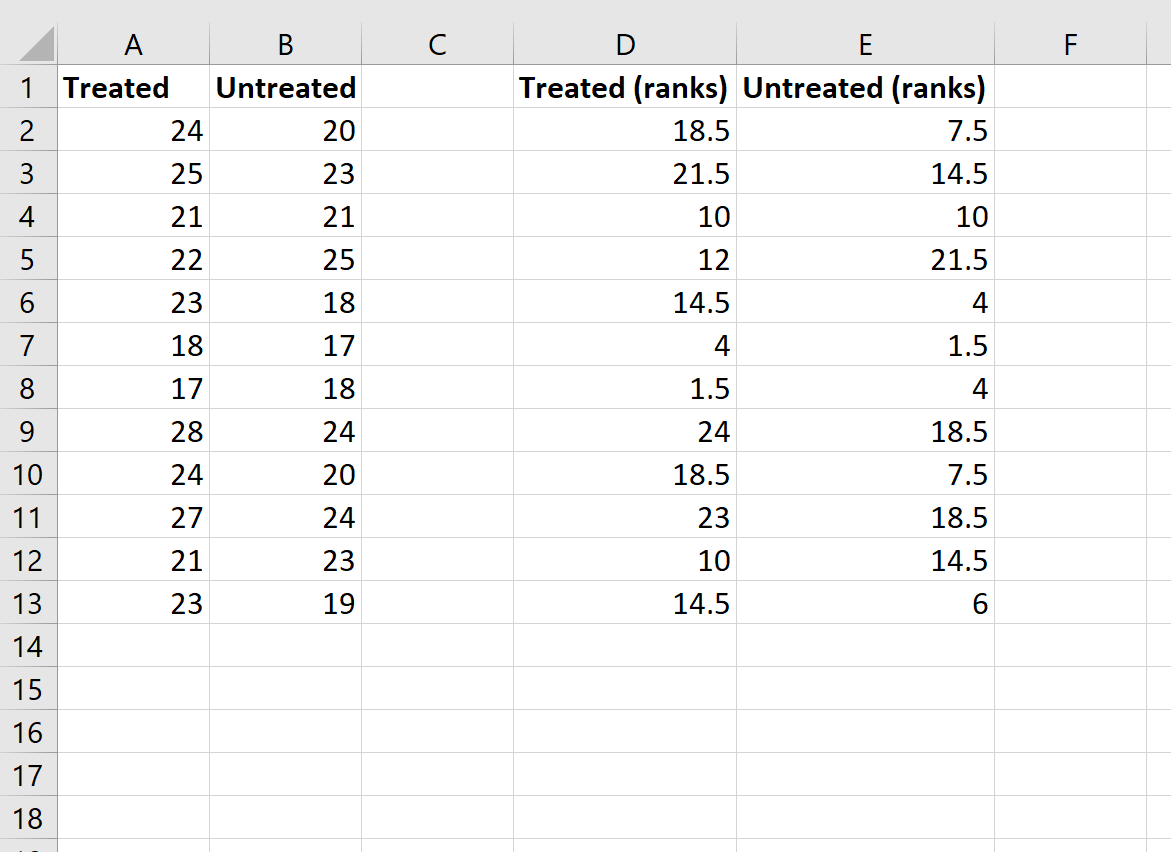
Étape 3 : Calculez les valeurs nécessaires pour la statistique de test.
Ensuite, nous utiliserons les formules suivantes pour calculer la somme des classements pour chaque groupe, la taille de l’échantillon pour chaque groupe, la statistique du test U pour chaque groupe et la statistique globale du test U :
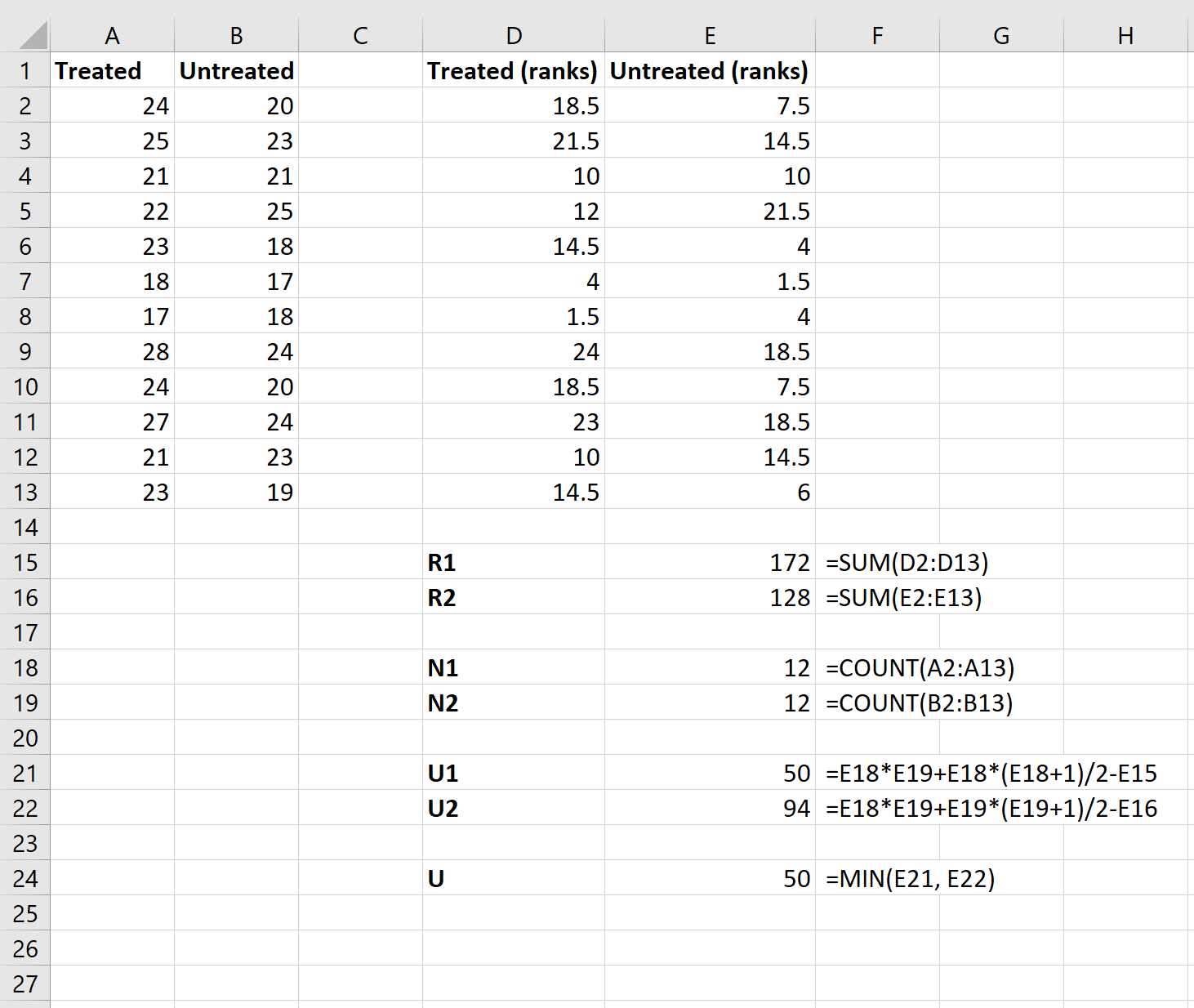
Étape 4 : Calculez la statistique du test z et la valeur p correspondante.
Enfin, nous utiliserons les formules suivantes pour calculer la statistique du test z et la valeur p correspondante afin de déterminer si nous devons rejeter ou non l’hypothèse nulle :
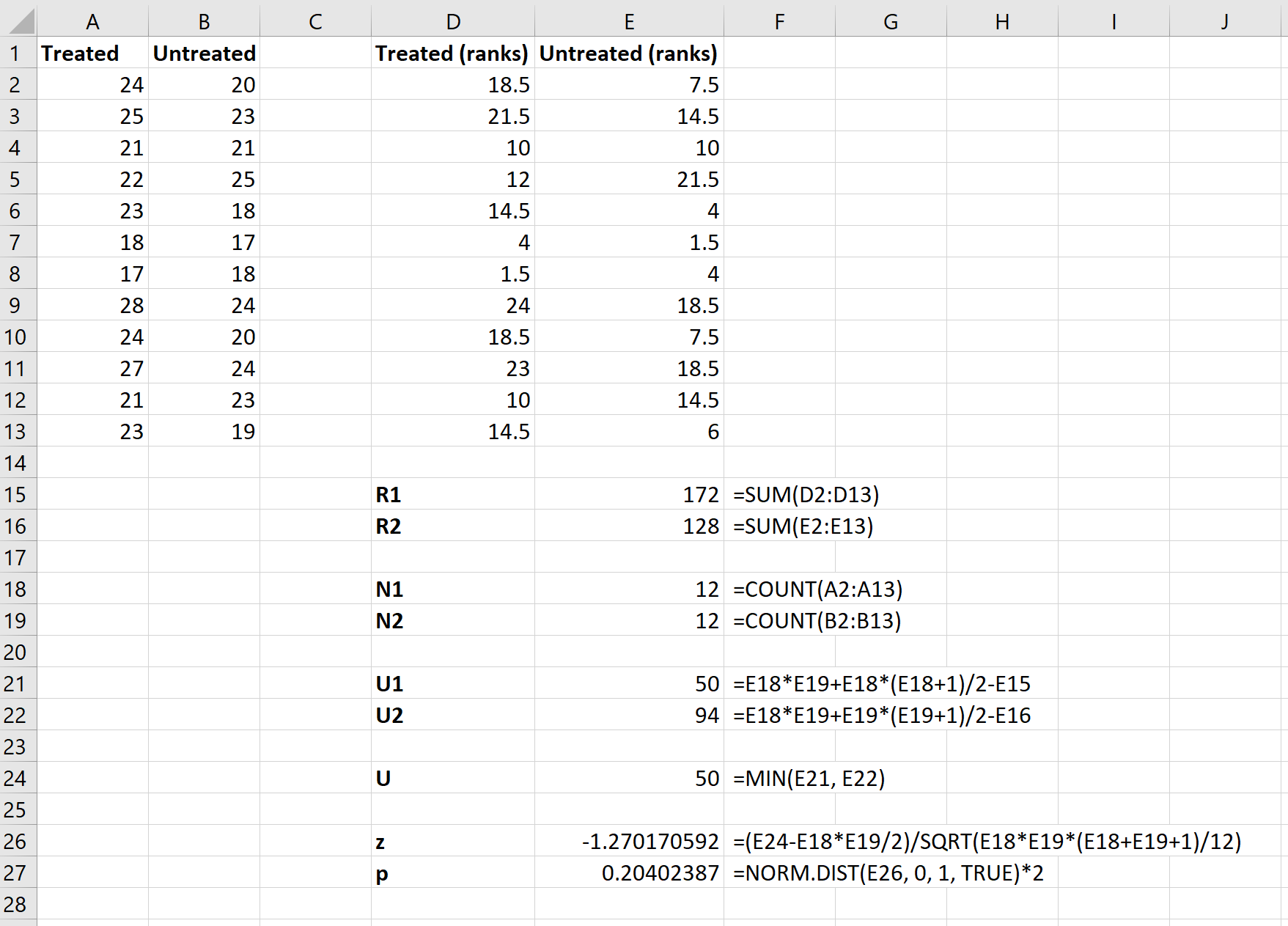
L’hypothèse nulle du test stipule que les deux groupes ont le même mpg moyen. Étant donné que la valeur p du test ( 0,20402387 ) n’est pas inférieure à notre niveau de signification de 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.
Nous n’avons pas suffisamment de preuves pour affirmer que le véritable mpg moyen est différent entre les deux groupes.
