Comment interpréter l’erreur standard résiduelle
L’ erreur type résiduelle est utilisée pour mesurer dans quelle mesure un modèle de régression s’adapte à un ensemble de données.
En termes simples, il mesure l’écart type des résidus dans un modèle de régression.
Il est calculé comme suit :
Erreur type résiduelle = √ Σ(y – ŷ) 2 /df
où:
- y : La valeur observée
- ŷ : La valeur prédite
- df : Les degrés de liberté, calculés comme le nombre total d’observations – nombre total de paramètres du modèle.
Plus l’erreur type résiduelle est petite, mieux un modèle de régression s’adapte à un ensemble de données. À l’inverse, plus l’erreur type résiduelle est élevée, moins le modèle de régression s’adapte à un ensemble de données.
Un modèle de régression qui a une petite erreur type résiduelle aura des points de données étroitement regroupés autour de la droite de régression ajustée :
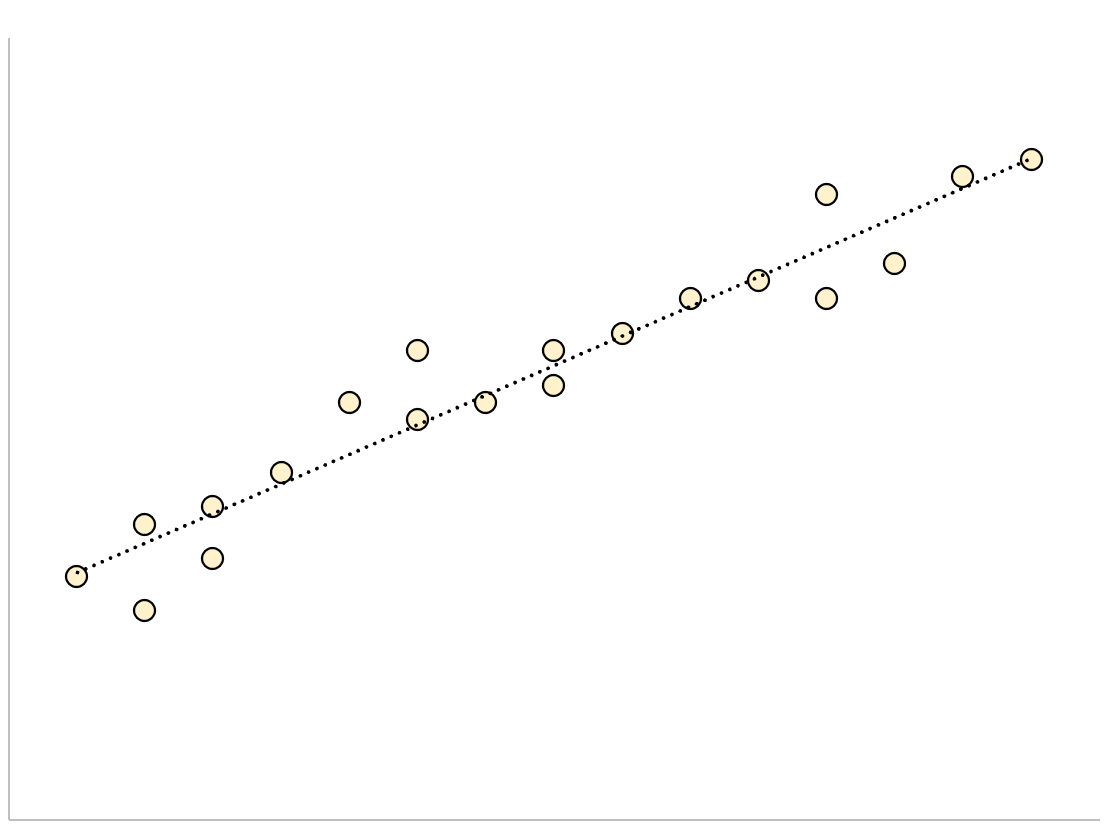
Les résidus de ce modèle (la différence entre les valeurs observées et les valeurs prédites) seront faibles, ce qui signifie que l’erreur type résiduelle sera également faible.
À l’inverse, un modèle de régression qui présente une erreur type résiduelle importante aura des points de données plus vaguement dispersés autour de la droite de régression ajustée :
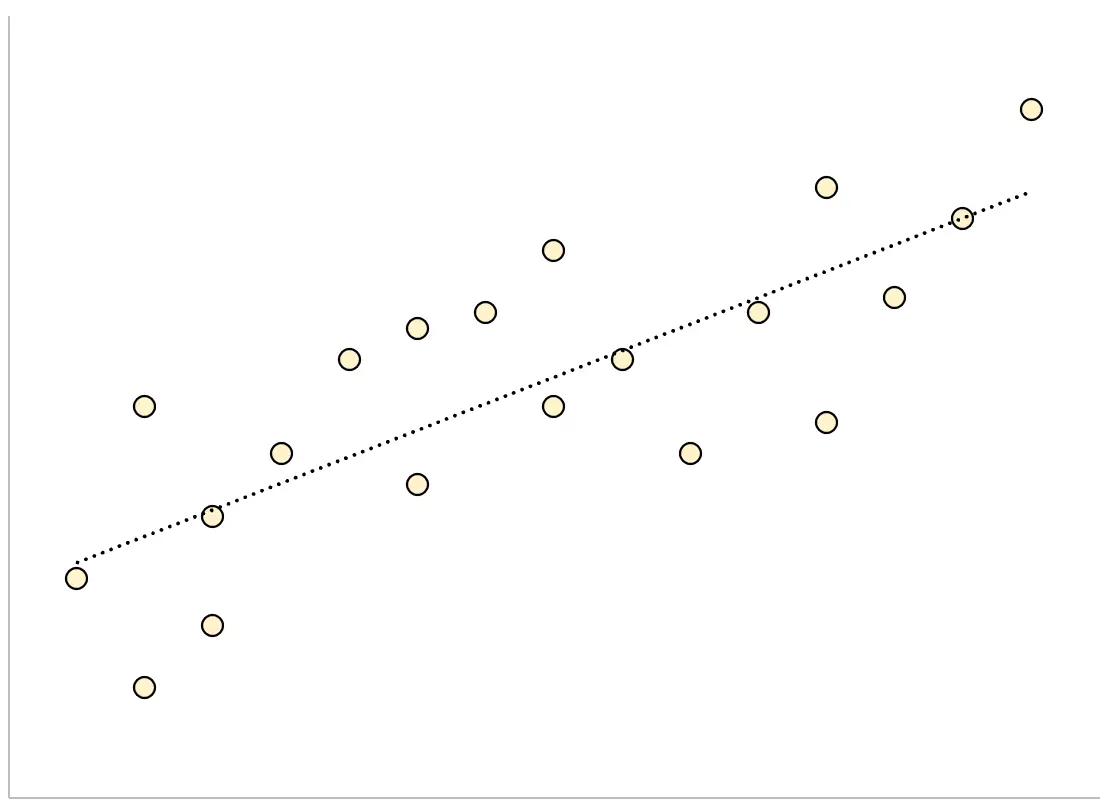
Les résidus de ce modèle seront plus grands, ce qui signifie que l’erreur type résiduelle sera également plus grande.
L’exemple suivant montre comment calculer et interpréter l’erreur type résiduelle d’un modèle de régression dans R.
Exemple : Interprétation de l’erreur type résiduelle
Supposons que nous souhaitions adapter le modèle de régression linéaire multiple suivant :
mpg = β 0 + β 1 (déplacement) + β 2 (puissance)
Ce modèle utilise les variables prédictives « déplacement » et « puissance » pour prédire les miles par gallon parcourus par une voiture donnée.
Le code suivant montre comment adapter ce modèle de régression dans R :
#load built-in mtcars dataset data(mtcars) #fit regression model model <- lm(mpg~disp+hp, data=mtcars) #view model summary summary(model) Call: lm(formula = mpg ~ disp + hp, data = mtcars) Residuals: Min 1Q Median 3Q Max -4.7945 -2.3036 -0.8246 1.8582 6.9363 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 30.735904 1.331566 23.083 < 2e-16 *** disp -0.030346 0.007405 -4.098 0.000306 *** hp -0.024840 0.013385 -1.856 0.073679 . --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.127 on 29 degrees of freedom Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
Vers le bas du résultat, nous pouvons voir que l’erreur type résiduelle de ce modèle est de 3,127 .
Cela nous indique que le modèle de régression prédit le mpg des voitures avec une erreur moyenne d’environ 3,127.
Utilisation de l’erreur standard résiduelle pour comparer des modèles
L’erreur type résiduelle est particulièrement utile pour comparer l’ajustement de différents modèles de régression.
Par exemple, supposons que nous ajustions deux modèles de régression différents pour prédire le mpg des voitures. L’erreur type résiduelle de chaque modèle est la suivante :
- Erreur type résiduelle du modèle 1 : 3,127
- Erreur type résiduelle du modèle 2 : 5,657
Étant donné que le modèle 1 a une erreur type résiduelle plus faible, il s’adapte mieux aux données que le modèle 2. Ainsi, nous préférerions utiliser le modèle 1 pour prédire le mpg des voitures, car les prédictions qu’il fait sont plus proches des valeurs mpg observées des voitures.
Ressources additionnelles
Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment créer un tracé résiduel dans R
