Comment interpréter l’erreur quadratique moyenne (RMSE)

L’analyse de régression est une technique que nous pouvons utiliser pour comprendre la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Une façon d’évaluer dans quelle mesure un modèle de régression s’adapte à un ensemble de données consiste à calculer l’ erreur quadratique moyenne , qui est une métrique qui nous indique la distance moyenne entre les valeurs prédites du modèle et les valeurs réelles de l’ensemble de données.

Plus le RMSE est bas, plus un modèle donné est capable de « s’adapter » à un ensemble de données.

La formule pour trouver l’erreur quadratique moyenne, souvent abrégée RMSE , est la suivante :

RMSE = √ Σ(P _je – O _je ) ² / n

où:

• Σ est un symbole fantaisiste qui signifie « somme »
• P _i est la valeur prédite pour la ^ième observation dans l’ensemble de données
• O _i est la valeur observée pour la ^ième observation dans l’ensemble de données
• n est la taille de l’échantillon

L’exemple suivant montre comment interpréter le RMSE pour un modèle de régression donné.

Exemple : Comment interpréter le RMSE pour un modèle de régression

Supposons que nous souhaitions construire un modèle de régression qui utilise les « heures étudiées » pour prédire la « note à l’examen » des étudiants à un examen d’entrée à l’université particulier.

Nous collectons les données suivantes pour 15 étudiants :

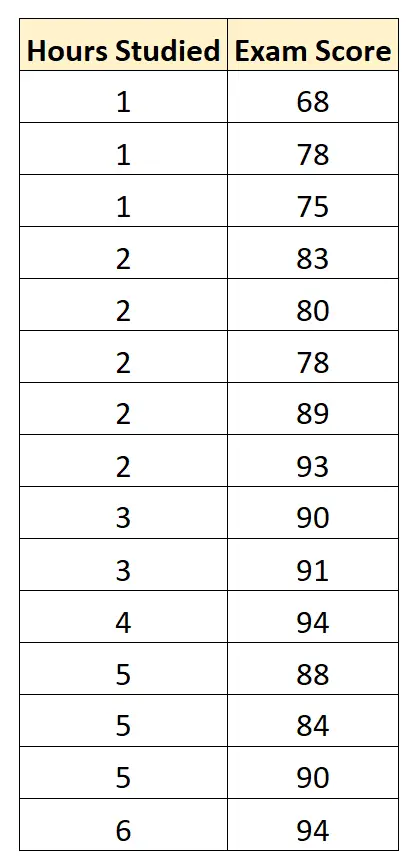
Nous utilisons ensuite des logiciels statistiques (comme Excel, SPSS, R, Python), etc. pour trouver le modèle de régression ajusté suivant :

Score d’examen = 75,95 + 3,08* (heures étudiées)

Nous pouvons ensuite utiliser cette équation pour prédire la note à l’examen de chaque étudiant, en fonction du nombre d’heures qu’il a étudié :

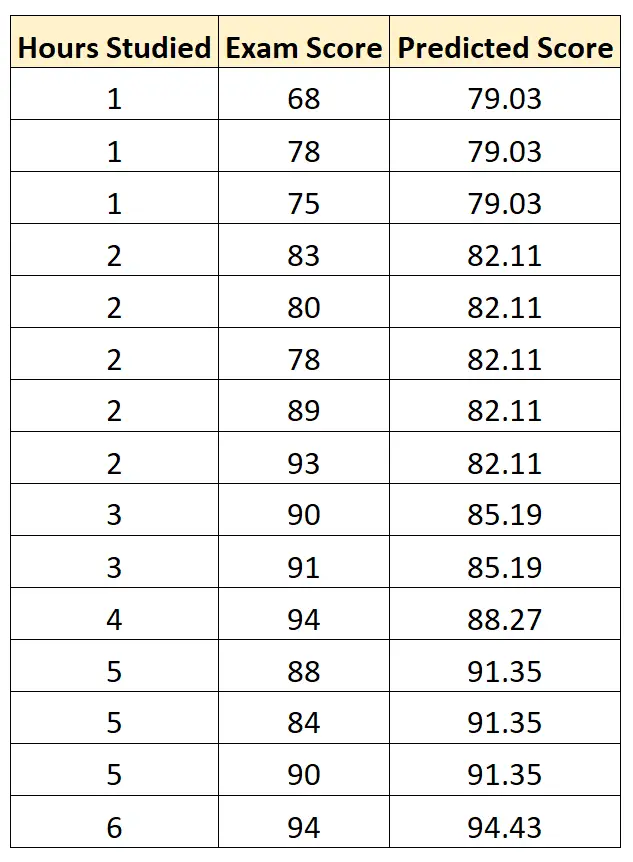
Nous pouvons ensuite calculer la différence au carré entre chaque note d’examen prévue et la note réelle de l’examen. On peut alors prendre la racine carrée de la moyenne de ces différences :

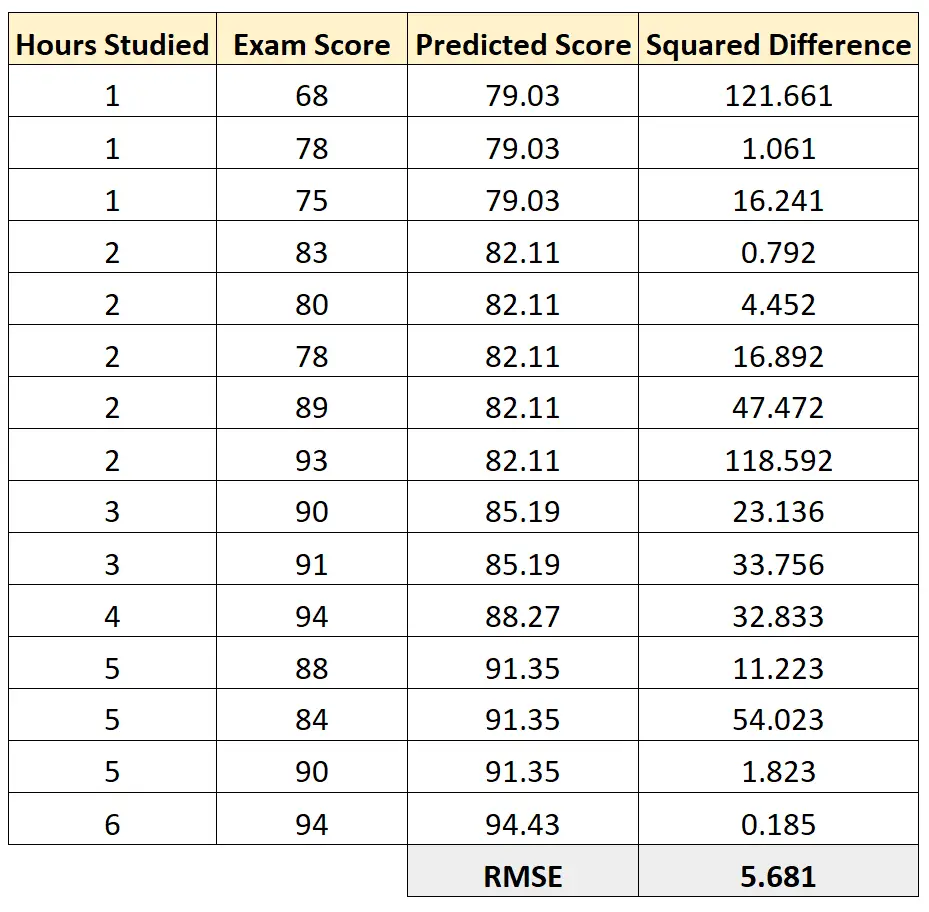
Le RMSE de ce modèle de régression s’avère être de 5,681 .

Rappelons que les résidus d’un modèle de régression sont les différences entre les valeurs des données observées et les valeurs prédites du modèle.

Résiduel = (P _i – O _i )

où

• P _i est la valeur prédite pour la ^ième observation dans l’ensemble de données
• O _i est la valeur observée pour la ^ième observation dans l’ensemble de données

Et rappelons que le RMSE d’un modèle de régression est calculé comme suit :

RMSE = √ Σ(P _je – O _je ) ² / n

Cela signifie que le RMSE représente la racine carrée de la variance des résidus.

C’est une valeur utile à connaître car elle nous donne une idée de la distance moyenne entre les valeurs de données observées et les valeurs de données prédites.

Cela contraste avec le R au carré du modèle, qui nous indique la proportion de la variance de la variable de réponse qui peut être expliquée par la ou les variables prédictives du modèle.

Comparaison des valeurs RMSE de différents modèles

Le RMSE est particulièrement utile pour comparer l’ajustement de différents modèles de régression.

Par exemple, supposons que nous souhaitions construire un modèle de régression pour prédire les résultats des examens des étudiants et que nous souhaitions trouver le meilleur modèle possible parmi plusieurs modèles potentiels.

Supposons que nous ajustions trois modèles de régression différents et trouvions leurs valeurs RMSE correspondantes :

• RMSE du modèle 1 : 14,5
• RMSE du modèle 2 : 16,7
• RMSE du modèle 3 : 9,8

Le modèle 3 a le RMSE le plus bas, ce qui nous indique qu’il est capable d’adapter au mieux l’ensemble de données parmi les trois modèles potentiels.

Ressources additionnelles

Calculateur RMSE
Comment calculer le RMSE dans Excel
Comment calculer le RMSE dans R
Comment calculer le RMSE en Python