Comment lire le tableau de distribution binomiale

La table de distribution binomiale   est un tableau qui montre les probabilités associées à la distribution binomiale . Pour utiliser la table de distribution binomiale, vous n’avez besoin que de trois valeurs :

• n : le nombre d’essais
• r : le nombre de « réussites » lors de n essais
• p : la probabilité de succès d’un essai donné

En utilisant ces trois nombres, vous pouvez utiliser la table de distribution binomiale pour trouver la probabilité d’obtenir exactement r succès au cours de n essais lorsque la probabilité de succès à chaque essai est p .

Les exemples suivants illustrent comment lire la table de distribution binomiale.

Exemple 1

Question : Jessica réussit 60 % de ses tentatives de lancer franc. Si elle réussit 6 lancers francs, quelle est la probabilité qu’elle en fasse exactement 4 ?

Pour répondre à cette question, nous pouvons rechercher la valeur dans le tableau de distribution binomiale qui correspond à n = 6, r = 4 et p = 0,60 :

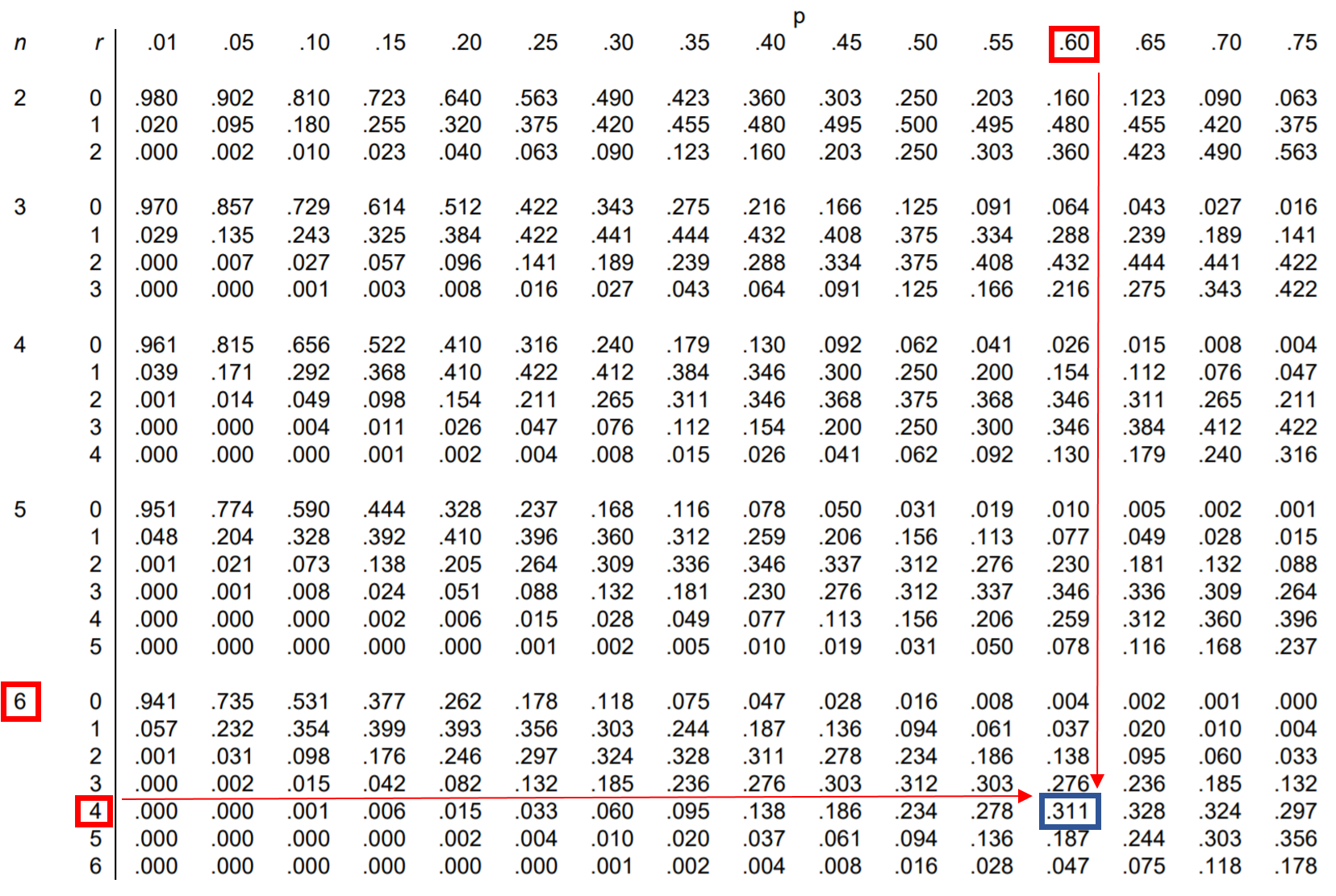
La probabilité que Jessica réussisse exactement 4 lancers francs sur 6 est de 0,311 .

Exemple 2

Question : Jessica réussit 60 % de ses tentatives de lancer franc. Si elle réussit 6 lancers francs, quelle est la probabilité qu’elle en fasse moins de 4 ?

Pour trouver cette probabilité, il faut en fait additionner les probabilités suivantes :

P(fait moins de 4) = P(fait 0) + P(fait 1) + P(fait 2) + P(fait 3)

Ainsi, nous pouvons rechercher chacune de ces quatre probabilités dans le tableau de distribution binomiale et les additionner :

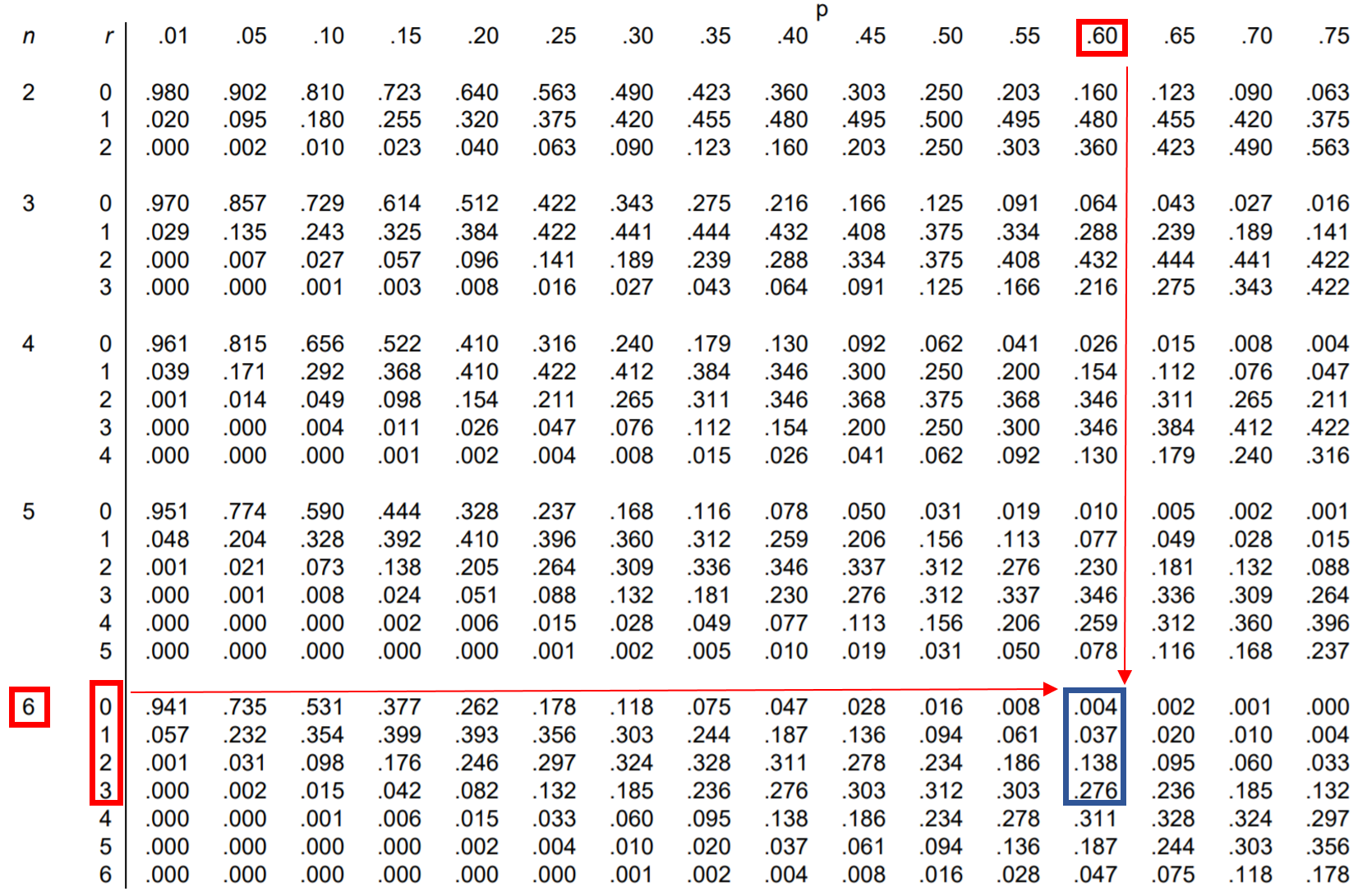
D’après le tableau, P(fait moins de 4) = .004 + .037 + .138 + .276 = 0.455 .

La probabilité que Jessica réalise moins de 4 lancers francs est de 0,455 .

Exemple 3

Question : Jessica réussit 60 % de ses tentatives de lancer franc. Si elle réussit 6 lancers francs, quelle est la probabilité qu’elle en réalise 4 ou plus ?

Pour trouver cette probabilité, il faut additionner les probabilités suivantes :

P(fait 4 ou plus) = P(fait 4) + P(fait 5) + P(fait 6)

Ainsi, nous pouvons rechercher chacune de ces trois probabilités dans le tableau de distribution binomiale et les additionner :

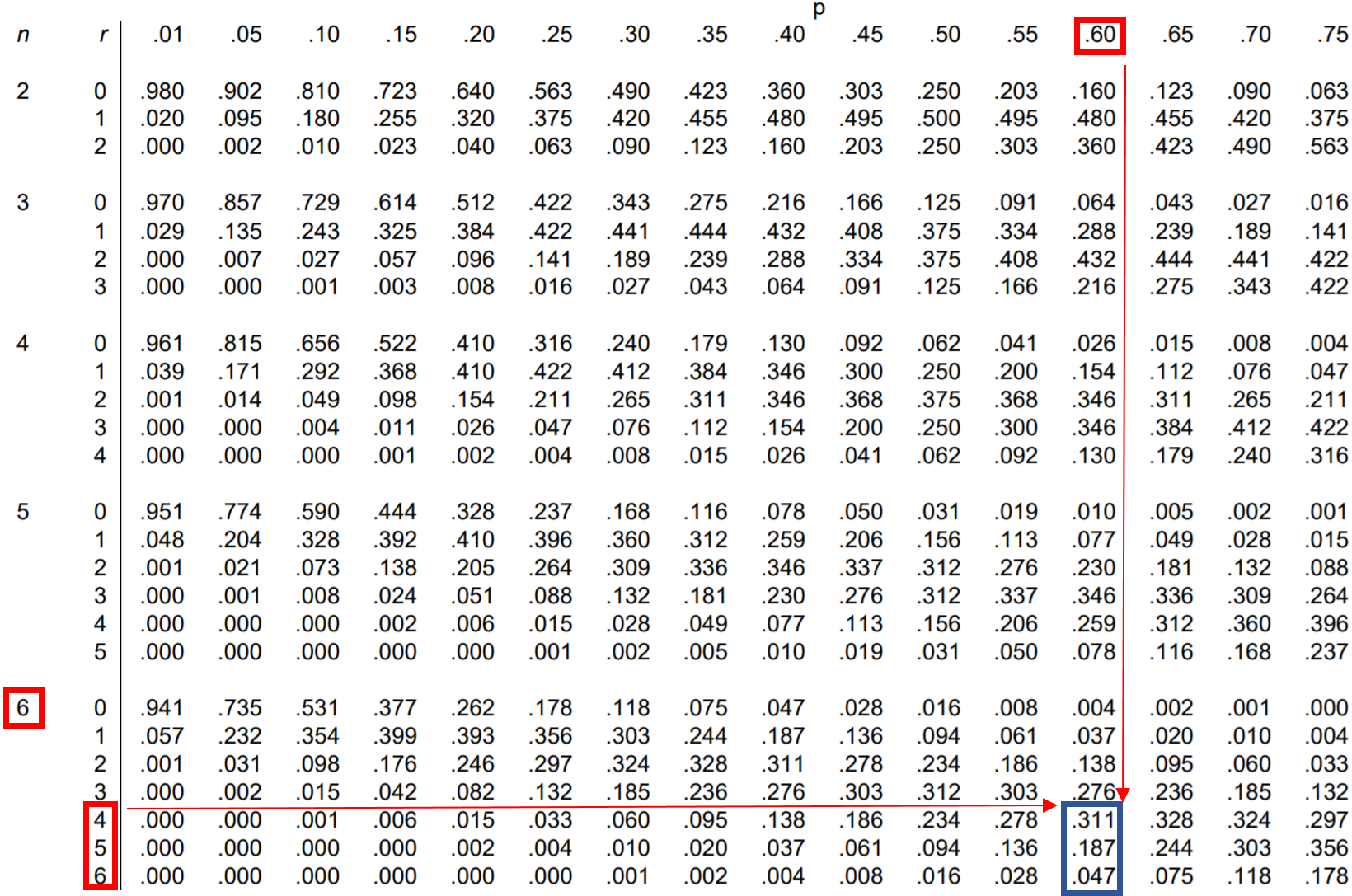
D’après le tableau, P(fait 4 ou plus) = .311 + .187 + .047 = 0.545 .

La probabilité que Jessica réalise 4 lancers francs ou plus est de 0,545 .