Comment lire une matrice de corrélation

En statistiques, nous cherchons souvent à comprendre la relation entre deux variables.

Par exemple, nous pourrions vouloir comprendre la relation entre le nombre d’heures d’études d’un étudiant et la note qu’il obtient à l’examen.

Une façon de quantifier cette relation consiste à utiliser le coefficient de corrélation de Pearson , qui est une mesure de l’association linéaire entre deux variables . Il a une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Plus le coefficient de corrélation s’éloigne de zéro, plus la relation entre les deux variables est forte.

Connexes : Qu’est-ce qui est considéré comme une corrélation « forte » ?

Mais dans certains cas, nous souhaitons comprendre la corrélation entre plusieurs paires de variables. Dans ces cas, nous pouvons créer une matrice de corrélation , qui est un tableau carré qui montre les coefficients de corrélation entre plusieurs variables.

Exemple de matrice de corrélation

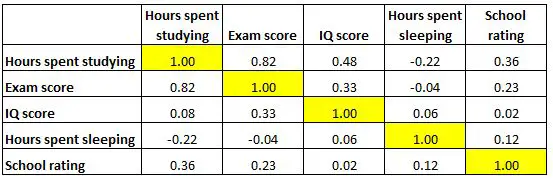
La matrice de corrélation ci-dessous présente les coefficients de corrélation entre plusieurs variables liées à l’éducation :

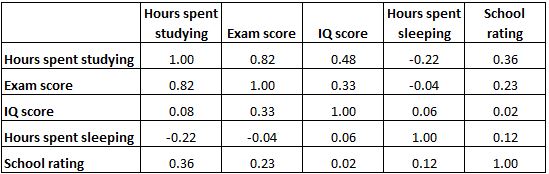
Chaque cellule du tableau montre la corrélation entre deux variables spécifiques. Par exemple, la cellule en surbrillance ci-dessous montre que la corrélation entre les « heures passées à étudier » et la « note à l’examen » est de 0,82 , ce qui indique qu’ils sont fortement corrélés positivement. Plus d’heures consacrées à étudier sont étroitement liées à des résultats aux examens plus élevés.

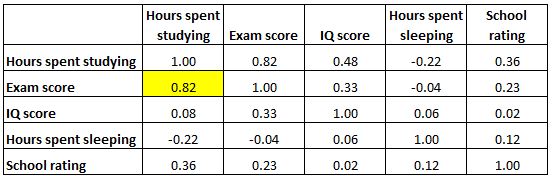
Et la cellule en surbrillance ci-dessous montre que la corrélation entre les « heures passées à étudier » et les « heures passées à dormir » est de -0,22 , ce qui indique qu’elles sont faiblement corrélées négativement. Plus d’heures passées à étudier sont associées à moins d’heures passées à dormir.

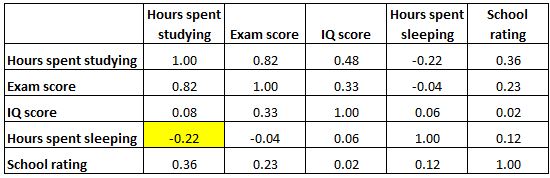
Et la cellule en surbrillance ci-dessous montre que la corrélation entre les « heures passées à dormir » et le « score de QI » est de 0,06 , ce qui indique qu’ils ne sont fondamentalement pas corrélés. Il existe très peu d’association entre le nombre d’heures de sommeil d’un élève et son score de QI.

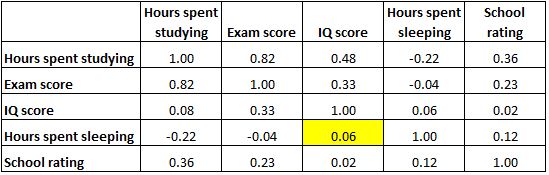
Notez également que les coefficients de corrélation le long de la diagonale du tableau sont tous égaux à 1 car chaque variable est parfaitement corrélée avec elle-même. Ces cellules ne sont pas utiles pour l’interprétation.

Variations de la matrice de corrélation

Notez qu’une matrice de corrélation est parfaitement symétrique. Par exemple, la cellule en haut à droite affiche exactement la même valeur que la cellule en bas à gauche :

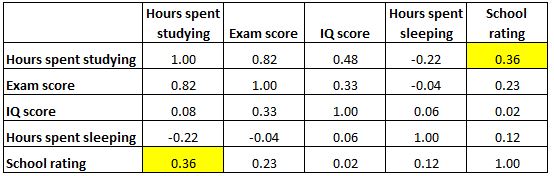
En effet, les deux cellules mesurent la corrélation entre les « heures passées à étudier » et la « note scolaire ».

Une matrice de corrélation étant symétrique, la moitié des coefficients de corrélation affichés dans la matrice sont redondants et inutiles. Ainsi, parfois seule la moitié de la matrice de corrélation sera affichée :

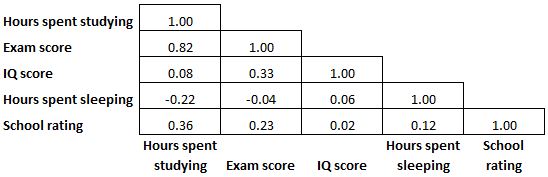
Et parfois, une matrice de corrélation sera colorée comme une carte thermique pour rendre les coefficients de corrélation encore plus faciles à lire :

Quand utiliser une matrice de corrélation

En pratique, une matrice de corrélation est couramment utilisée pour trois raisons :

1. Une matrice de corrélation résume commodément un ensemble de données.

Une matrice de corrélation est un moyen simple de résumer les corrélations entre toutes les variables d’un ensemble de données. Par exemple, supposons que nous disposions de l’ensemble de données suivant contenant les informations suivantes pour 1 000 étudiants :

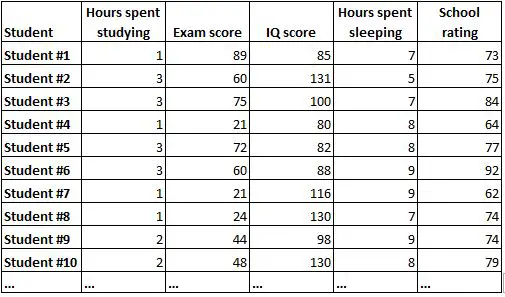
Il serait très difficile de comprendre la relation entre chaque variable en regardant simplement les données brutes. Heureusement, une matrice de corrélation peut nous aider à comprendre rapidement les corrélations entre chaque paire de variables.

2. Une matrice de corrélation sert de diagnostic pour la régression.

L’une des hypothèses clés de la régression linéaire multiple est qu’aucune variable indépendante du modèle n’est fortement corrélée à une autre variable du modèle.

Lorsque deux variables indépendantes sont fortement corrélées, cela entraîne un problème appelé multicolinéarité et peut rendre difficile l’interprétation des résultats de la régression.

L’un des moyens les plus simples de détecter un problème potentiel de multicolinéarité consiste à examiner une matrice de corrélation et à vérifier visuellement si l’une des variables est fortement corrélée les unes aux autres.

3. Une matrice de corrélation peut être utilisée comme entrée dans d’autres analyses.

Une matrice de corrélation est utilisée comme entrée pour d’autres analyses complexes telles que l’analyse factorielle exploratoire et les modèles d’équations structurelles.

Ressources additionnelles

Les didacticiels suivants expliquent comment créer une matrice de corrélation à l’aide de divers logiciels statistiques :

Comment créer une matrice de corrélation dans Excel
Comment créer une matrice de corrélation dans SPSS
Comment créer une matrice de corrélation dans Stata
Comment créer une matrice de corrélation en Python