Comment utiliser la table Z (avec exemples)
Une table z est une table qui vous indique quel pourcentage de valeurs tombe en dessous d’un certain score z dans une distribution normale standard.
Un score z vous indique simplement de combien d’écarts types une valeur de donnée individuelle tombe par rapport à la moyenne. Il est calculé comme suit :
Score z = (x – μ) / σ
où:
- x : valeur de donnée individuelle
- μ : moyenne de la population
- σ : écart type de la population
Ce didacticiel montre plusieurs exemples d’utilisation de la table z.
Exemple 1
Les scores à un certain examen d’entrée à l’université sont normalement distribués avec une moyenne μ = 82 et un écart type σ = 8. Environ quel pourcentage d’étudiants obtiennent un score inférieur à 84 à l’examen ?
Étape 1 : Trouvez le score z.
Tout d’abord, nous trouverons le z-score associé à un score à l’examen de 84 :
Score z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25
Étape 2 : Utilisez le tableau z pour trouver le pourcentage qui correspond au score z.
Ensuite, nous rechercherons la valeur 0,25 dans la table z :

Environ 59,87 % des étudiants obtiennent un score inférieur à 84 à cet examen.
Exemple 2
La hauteur des plantes dans un certain jardin est normalement distribuée avec une moyenne de μ = 26,5 pouces et un écart type de σ = 2,5 pouces. Environ quel pourcentage de plantes mesurent plus de 26 pouces de hauteur ?
Étape 1 : Trouvez le score z.
Dans un premier temps, nous retrouverons le z-score associé à une hauteur de 26 pouces.
Score z = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2
Étape 2 : Utilisez le tableau z pour trouver le pourcentage qui correspond au score z.
Ensuite, nous rechercherons la valeur -0,2 dans la table z :
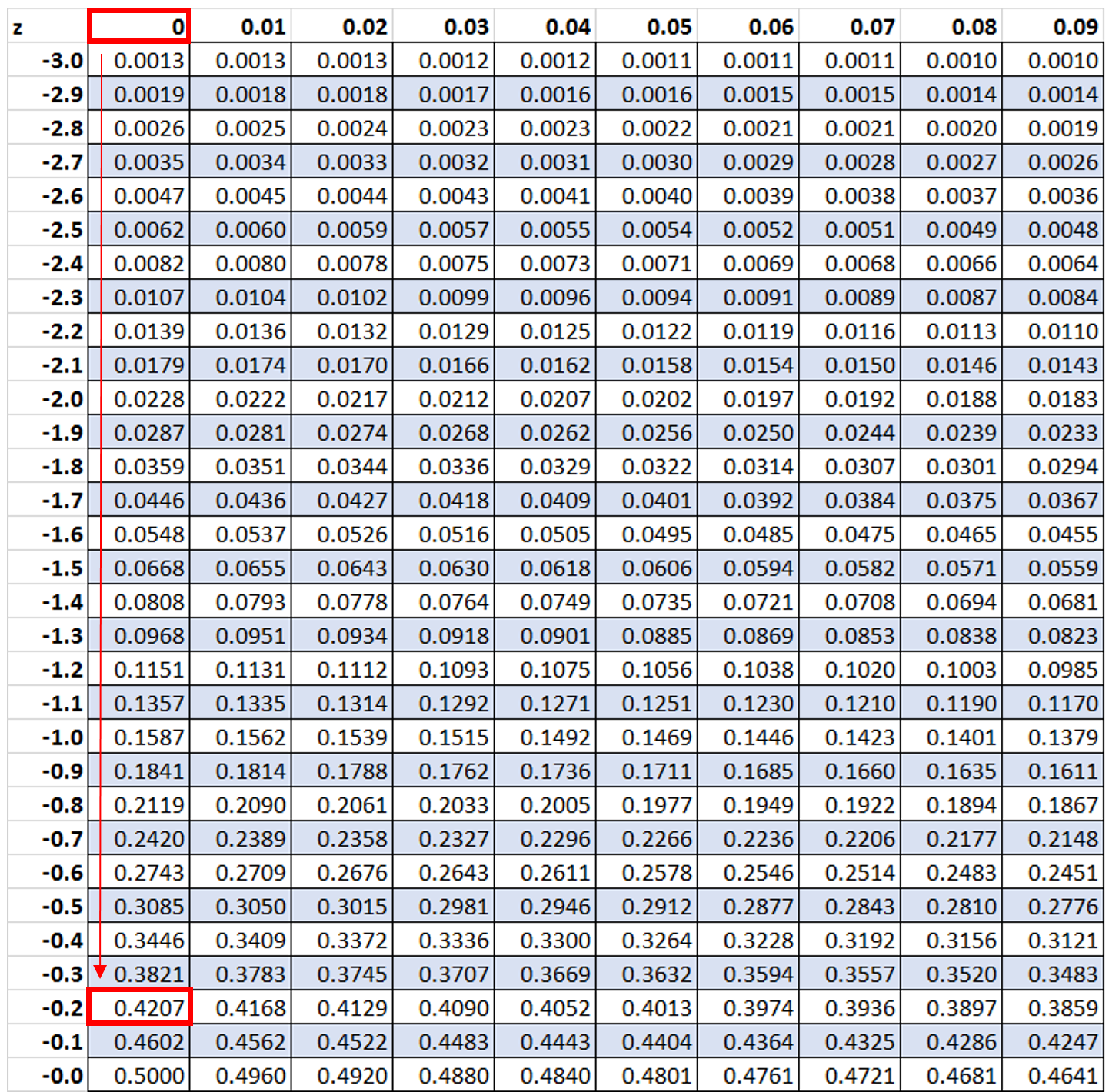
Nous constatons que 42,07 % des valeurs sont inférieures à un z-score de -0,2. Cependant, dans cet exemple, nous voulons savoir quel pourcentage de valeurs est supérieur à -0,2, ce que nous pouvons trouver en utilisant la formule 100 % – 42,07 % = 57,93 %.
Ainsi, environ 59,87 % des plantes de ce jardin mesurent plus de 26 pouces de hauteur.
Exemple 3
Le poids d’une certaine espèce de dauphin est normalement distribué avec une moyenne de μ = 400 livres et un écart type de σ = 25 livres. Environ quel pourcentage de dauphins pèsent entre 410 et 425 livres ?
Étape 1 : Trouvez les scores z.
Dans un premier temps, nous retrouverons les z-scores associés à 410 livres et 425 livres
Score z de 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4
Score z de 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1
Étape 2 : Utilisez le tableau z pour trouver les pourcentages qui correspondent à chaque score z.
Tout d’abord, nous rechercherons la valeur 0,4 dans la table z :

Ensuite, nous rechercherons la valeur 1 dans la table z :

Enfin, nous soustrairons la plus petite valeur de la plus grande valeur : 0,8413 – 0,6554 = 0,1859 .
Ainsi, environ 18,59 % des dauphins pèsent entre 410 et 425 livres.
Ressources additionnelles
Une introduction à la distribution normale
Calculateur de zone de distribution normale
Calculateur de score Z
