Comment comparer les boîtes à moustaches : avec des exemples

Une boîte à moustaches est un type de tracé qui affiche le résumé à cinq chiffres d’un ensemble de données, qui comprend :

• La valeur minimale
• Le premier quartile (le 25e centile)
• La valeur médiane
• Le troisième quartile (le 75e percentile)
• La valeur maximale

Pour réaliser un box plot, nous dessinons une boîte du premier au troisième quartile. Ensuite, nous traçons une ligne verticale au niveau de la médiane. Enfin, nous dessinons des « moustaches » des quartiles jusqu’à la valeur minimale et maximale.

Les boîtes à moustaches sont utiles car elles nous permettent de comprendre rapidement la distribution des valeurs dans un ensemble de données. Ils sont également utiles pour comparer deux ensembles de données différents.

Lorsque l’on compare deux ou plusieurs boîtes à moustaches, nous pouvons répondre à quatre questions différentes :

1. Comment les valeurs médianes se comparent-elles ? Nous pouvons comparer la ligne verticale dans chaque case pour déterminer quel ensemble de données a une valeur médiane la plus élevée.

2. Comment se compare la dispersion ? Nous pouvons comparer la longueur de chaque case (qui représente la distance entre Q1 et Q3 – l’intervalle interquartile) pour déterminer quel ensemble de données est le plus étendu.

3. Comment l’asymétrie se compare-t-elle ? Plus la ligne verticale est proche du premier trimestre, plus l’ensemble de données est positivement asymétrique. Plus la ligne verticale est proche du troisième trimestre, plus l’ensemble de données est asymétrique.

4. Des valeurs aberrantes sont-elles présentes ? Dans les diagrammes en boîte, les valeurs aberrantes sont généralement représentées par de minuscules cercles qui s’étendent au-delà de chaque moustache. Une observation est définie comme étant aberrante si elle répond à l’un des critères suivants :

• Une observation est inférieure à Q1 – 1,5*IQR
• Une observation est supérieure à Q3 + 1,5*IQR

L’exemple suivant montre comment comparer deux boîtes à moustaches différentes et répondre à ces quatre questions.

Exemple : comparaison de boîtes à moustaches

Les ensembles de données suivants affichent les résultats des étudiants qui ont utilisé l’une des deux techniques d’étude pour se préparer à l’examen :

Méthode 1 : 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91

Méthode 2 : 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98

Si nous créons des boîtes à moustaches pour chaque ensemble de données, voici à quoi elles ressembleraient :

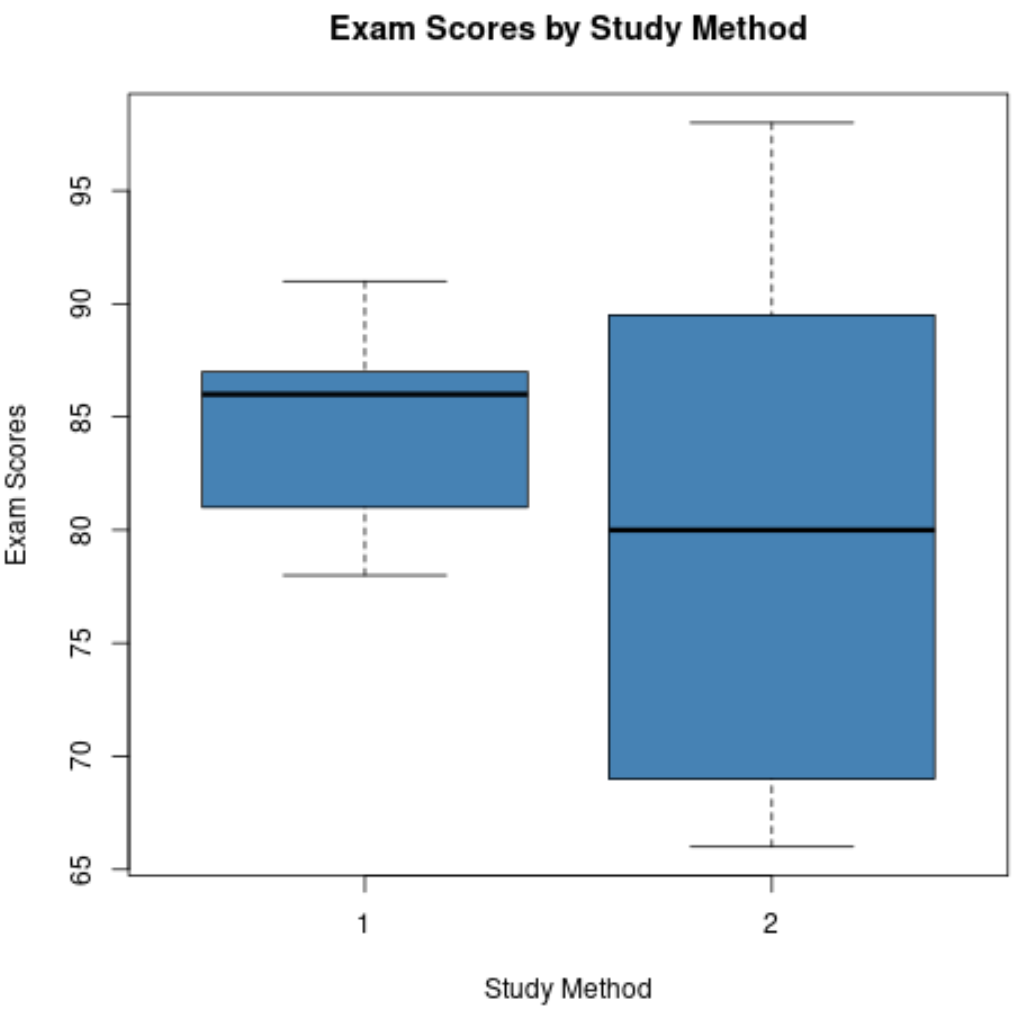
Nous pouvons comparer ces deux boîtes à moustaches et répondre aux quatre questions suivantes :

1. Comment les valeurs médianes se comparent-elles ? La ligne au milieu du diagramme en boîte pour la méthode d’étude 1 est plus haute que la ligne pour la méthode d’étude 2, ce qui indique que les étudiants qui ont utilisé la méthode d’étude 1 ont obtenu une note médiane à l’examen plus élevée.

2. Comment se compare la dispersion ? Le diagramme en boîte de la méthode d’étude 2 est beaucoup plus long que celui de la méthode d’étude 1, ce qui indique que les résultats des examens sont beaucoup plus répartis parmi les étudiants qui ont utilisé la méthode d’étude 2.

3. Comment l’asymétrie se compare-t-elle ? La ligne au milieu du diagramme en boîte pour la méthode d’étude 1 est proche de Q3, ce qui indique que la distribution des résultats aux examens des étudiants qui ont utilisé la méthode d’étude 1 est négativement asymétrique. À l’inverse, la ligne au milieu du diagramme en boîte pour la méthode d’étude 2 est proche du centre de la boîte, ce qui signifie que la distribution des scores est peu asymétrique.

4. Des valeurs aberrantes sont-elles présentes ? Aucune des deux boîtes à moustaches ne comporte de minuscules cercles qui s’étendent au-delà des moustaches supérieures ou inférieures, ce qui signifie qu’aucun des deux ensembles de données ne présente de valeurs aberrantes claires.

Ressources additionnelles

Comment créer et interpréter des boîtes à moustaches dans Excel
Comment créer et interpréter des boîtes à moustaches dans SPSS
Comment créer plusieurs boîtes à moustaches dans R
Comment créer et interpréter des boîtes à moustaches dans Stata