Comparaison des scores Z de différentes distributions
Un score z vous indique de combien d’écarts types une valeur de donnée individuelle tombe par rapport à la moyenne. Il est calculé comme suit :
Score z = (x – μ) / σ
où:
- x : valeur de donnée individuelle
- μ : moyenne de la population
- σ : écart type de la population
Un score z pour une valeur individuelle peut être interprété comme suit :
- Score z positif : la valeur individuelle est supérieure à la moyenne.
- Score z négatif : la valeur individuelle est inférieure à la moyenne.
- Un z-score de 0 : la valeur individuelle est égale à la moyenne.
Les scores Z sont particulièrement utiles lorsque nous souhaitons comparer la position relative de deux points de données provenant de deux distributions différentes. Pour illustrer cela, considérons l’exemple suivant.
Exemple : comparaison des scores Z
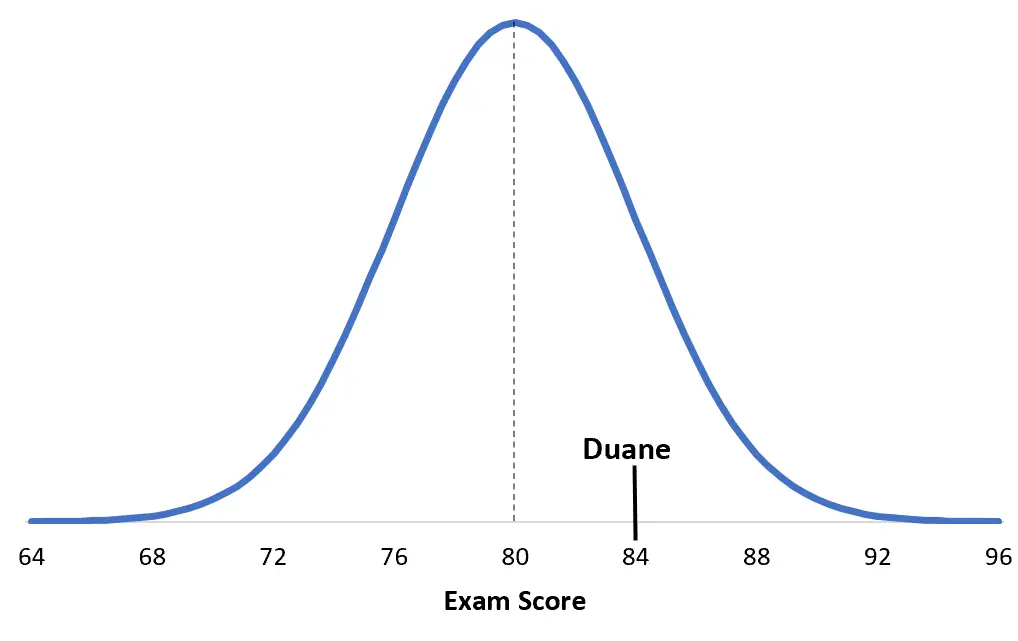
Les scores à un certain examen universitaire sont normalement distribués avec une moyenne μ = 80 et un écart type σ = 4. Duane obtient un 84 à cet examen.
Les scores à un autre examen universitaire sont normalement distribués avec une moyenne μ = 85 et un écart type σ = 8. Debbie obtient un 90 à cet examen.
Par rapport à leur propre répartition des notes aux examens, qui a obtenu les meilleurs résultats à leur examen ?
Pour répondre à cette question, nous pouvons calculer le z-score du score à l’examen de chaque personne :
Score z de Duane = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1
Score z de Debbie = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0,625
Bien que Debbie ait obtenu un score plus élevé, le score de Duane est en réalité plus élevé par rapport à la répartition de son examen particulier.
Pour comprendre cela, il est utile de visualiser la situation. Voici la note de Duane par rapport à la répartition de son examen particulier :
Et voici la note de Debbie par rapport à la répartition de son examen :
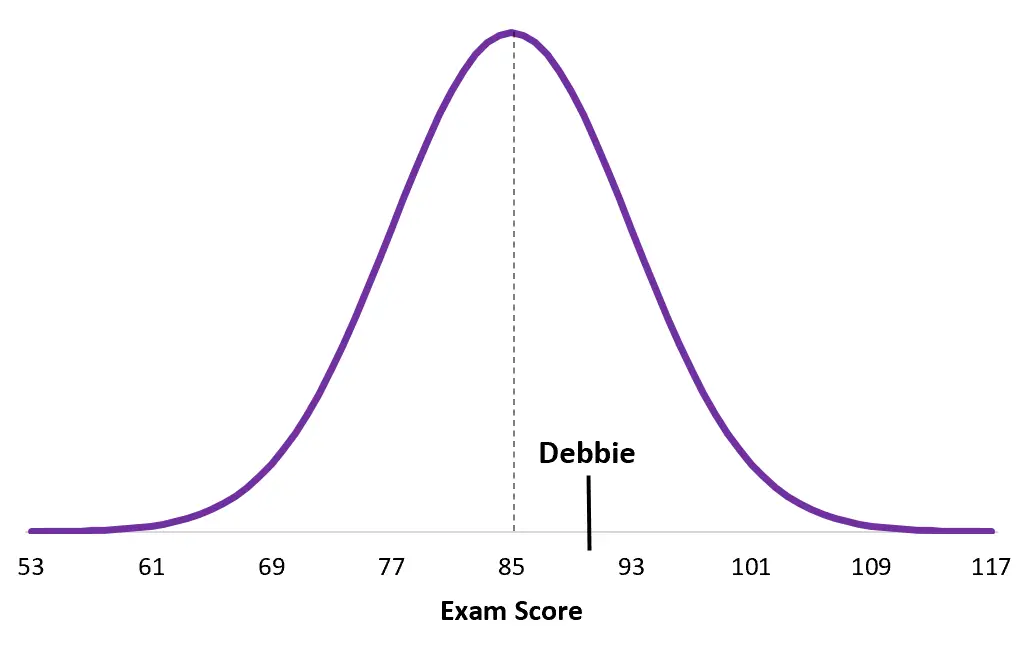
Remarquez à quel point le score de Debbie est plus proche de la moyenne de sa population que celui de Duane. Bien qu’elle ait un score globalement plus élevé, son score z est inférieur simplement parce que le score moyen à son examen particulier est plus élevé.
Cet exemple illustre pourquoi les scores z sont si utiles pour comparer les valeurs de données de différentes distributions : les scores z prennent en compte la moyenne et les écarts types des distributions, ce qui nous permet de comparer les valeurs de données de différentes distributions et de voir laquelle est la plus élevée par rapport à leurs propres distributions.
Ressources additionnelles
Calculateur de score Z
Comparez le calculateur de scores Z
