Comment calculer la corrélation entre les variables catégorielles

Nous utilisons souvent le coefficient de corrélation de Pearson pour calculer la corrélation entre des variables numériques continues.

Cependant, nous devons utiliser une métrique différente pour calculer la corrélation entre les variables catégorielles, c’est-à-dire les variables qui prennent des noms ou des étiquettes telles que :

• État civil (célibataire, marié, divorcé)
• Statut de fumeur (fumeur, non-fumeur)
• Couleur des yeux (bleu, marron, vert)

Il existe trois mesures couramment utilisées pour calculer la corrélation entre les variables catégorielles :

1. Corrélation tétrachorique : utilisée pour calculer la corrélation entre les variables catégorielles binaires.

2. Corrélation polychorique : utilisée pour calculer la corrélation entre les variables catégorielles ordinales.

3. V de Cramer : utilisé pour calculer la corrélation entre les variables catégorielles nominales.

Les sections suivantes fournissent un exemple de la façon de calculer chacune de ces trois mesures.

Métrique 1 : Corrélation tétrachorique

La corrélation tétrachorique est utilisée pour calculer la corrélation entre des variables catégorielles binaires. Rappelons que les variables binaires sont des variables qui ne peuvent prendre qu’une des deux valeurs possibles.

La valeur de la corrélation tétrachorique varie de -1 à 1, où -1 indique une forte corrélation négative, 0 indique une absence de corrélation et 1 indique une forte corrélation positive.

Par exemple, supposons que nous voulions savoir si le sexe est associé ou non à la préférence pour un parti politique. Nous prenons donc un échantillon aléatoire simple de 100 électeurs et les interrogeons sur leur préférence pour un parti politique.

Le tableau suivant présente les résultats de l’enquête :

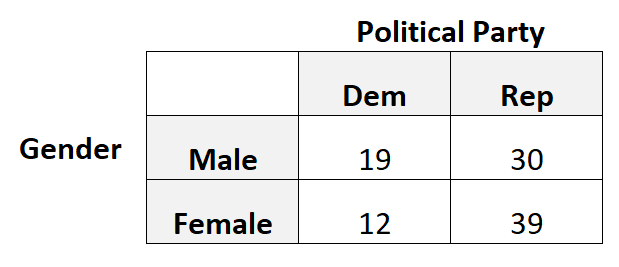
Nous utiliserions la corrélation tétrachorique dans ce scénario car chaque variable catégorielle est binaire, c’est-à-dire que chaque variable ne peut prendre que deux valeurs possibles.

Nous pouvons utiliser le code suivant dans R pour calculer la corrélation tétrachorique entre les deux variables :

library(psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow=2)

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

La corrélation tétrachorique s’avère être de 0,27 . Cette valeur est assez faible, ce qui indique qu’il existe une faible association (le cas échéant) entre le sexe et la préférence pour le parti politique.

Métrique 2 : Corrélation polychorique

La corrélation polychorique est utilisée pour calculer la corrélation entre les variables catégorielles ordinales. Rappelons que les variables ordinales sont des variables dont les valeurs possibles ont un ordre naturel.

La valeur de la corrélation polychorique varie de -1 à 1, où -1 indique une forte corrélation négative, 0 indique une absence de corrélation et 1 indique une forte corrélation positive.

Par exemple, supposons que vous vouliez savoir si deux agences de classification de films différentes ont une forte corrélation entre leurs classifications de films.

Nous demandons à chaque agence d’évaluer 20 films différents sur une échelle de 1 à 3, 1 indiquant « mauvais », 2 indiquant « médiocre » et 3 indiquant « bon ».

Le tableau suivant montre les résultats :

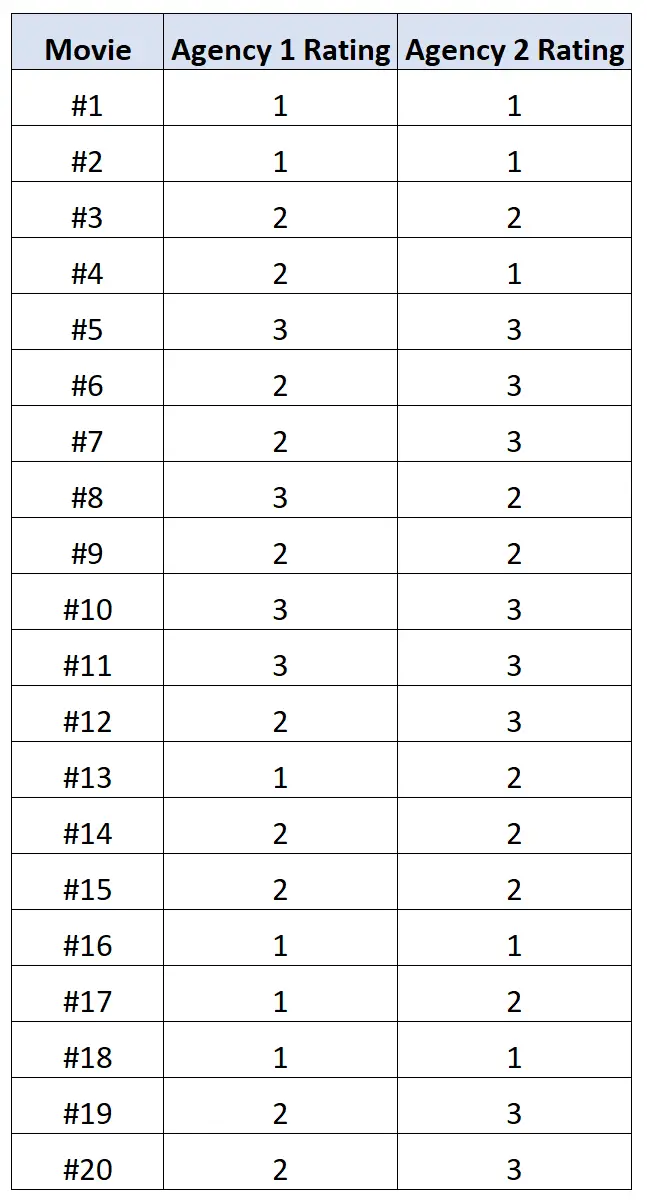
On peut utiliser le code suivant dans R pour calculer la corrélation polychorique entre les notes des deux agences :

library(polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

La corrélation polychorique s’avère être de 0,78 . Cette valeur est assez élevée, ce qui indique qu’il existe une forte association positive entre les notes de chaque agence.

Métrique 3 : V de Cramer

Le V de Cramer est utilisé pour calculer la corrélation entre les variables catégorielles nominales. Rappelez-vous que les variables nominales sont celles qui portent des étiquettes de catégorie mais n’ont pas d’ordre naturel.

La valeur du V de Cramer varie de 0 à 1, 0 indiquant aucune association entre les variables et 1 indiquant une forte association entre les variables.

Par exemple, supposons que nous souhaitions savoir s’il existe une corrélation entre la couleur des yeux et le sexe. Nous interrogeons donc 50 personnes et obtenons les résultats suivants :

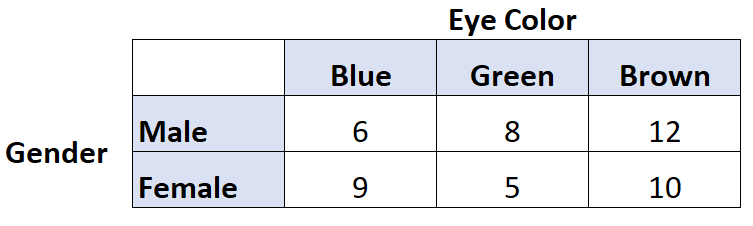
Nous pouvons utiliser le code suivant dans R pour calculer le V de Cramer pour ces deux variables :

library(rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow=2)

#view table
data

     [,1] [,2] [,3]
[1,]    6    8   12
[2,]    9    5   10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

Le V de Cramer s’avère être 0,1671 . Cette valeur est assez faible, ce qui indique qu’il existe une faible association entre le sexe et la couleur des yeux.

Ressources additionnelles

Introduction au coefficient de corrélation de Pearson
Introduction à la corrélation tétrachorique
Variables catégorielles ou quantitatives : quelle est la différence ?
Niveaux de mesure : nominal, ordinal, intervalle et rapport