Comment calculer la corrélation entre continu et & Variables catégorielles

Lorsque nous souhaitons calculer la corrélation entre deux variables continues, nous utilisons généralement le coefficient de corrélation de Pearson .

Cependant, lorsque nous souhaitons calculer la corrélation entre une variable continue et une variable catégorielle , nous pouvons utiliser ce qu’on appelle la corrélation bisériale ponctuelle .

La corrélation bisériale ponctuelle est utilisée pour calculer la corrélation entre une variable catégorielle binaire (une variable qui ne peut prendre que deux valeurs) et une variable continue et possède les propriétés suivantes :

• La corrélation bisériale ponctuelle peut varier entre -1 et 1.
• Pour chaque groupe créé par la variable binaire, on suppose que la variable continue est normalement distribuée avec des variances égales.
• Pour chaque groupe créé par la variable binaire, on suppose qu’il n’y a pas de valeurs aberrantes extrêmes.

L’exemple suivant montre comment calculer une corrélation bisériale ponctuelle dans la pratique.

Exemple : Calcul d’une corrélation bisériale ponctuelle

Supposons qu’un professeur d’université souhaite déterminer s’il existe une corrélation entre le sexe et le score à un examen d’aptitude particulier.

Il recueille les données suivantes sur 12 garçons et 12 filles de sa classe :

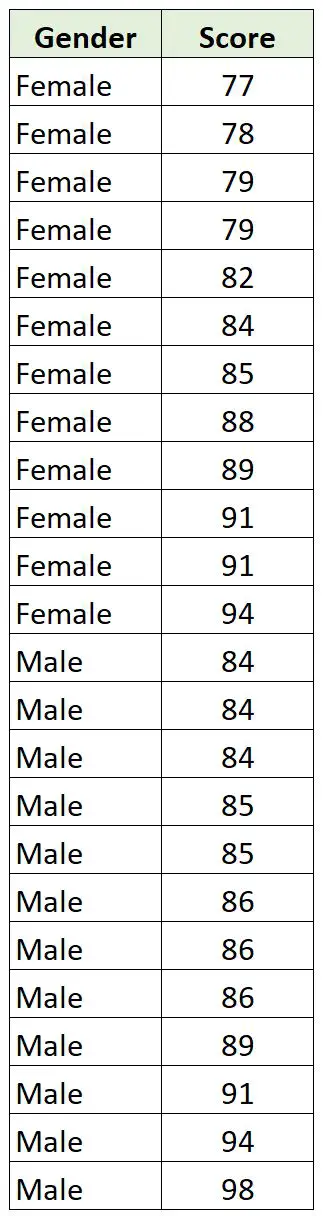
Étant donné que le sexe est une variable catégorielle et que le score est une variable continue, il est logique de calculer une corrélation point-bisérielle entre les deux variables.

Le professeur peut utiliser n’importe quel logiciel statistique (notamment Excel, R, Python, SPSS, Stata) pour calculer la corrélation point-bisériale entre les deux variables.

Le code suivant montre comment calculer la corrélation point-bisériale dans R, en utilisant la valeur 0 pour représenter les femmes et 1 pour représenter les hommes pour la variable de genre :

#define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
cor.test(gender, score)

	Pearson's product-moment correlation

data:  gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386  0.6147832
sample estimates:
      cor 
0.2810996 

À partir du résultat, nous pouvons voir que le coefficient de corrélation bisériale ponctuelle est de 0,281 et la valeur p correspondante est de 0,1833 .

Puisque le coefficient de corrélation est positif, cela nous indique qu’il existe une corrélation positive entre le sexe et le score.

Puisque nous avons codé les hommes comme 1 et les femmes comme 0, cela indique que les scores ont tendance à être plus élevés pour les hommes (c’est-à-dire que les scores ont tendance à augmenter à mesure que le sexe « augmente » de 0 à 1).

Cependant, puisque la valeur p n’est pas inférieure à 0,05, ce coefficient de corrélation n’est pas statistiquement significatif.

Ressources additionnelles

Les didacticiels suivants expliquent comment calculer la corrélation bisériale ponctuelle à l’aide de différents logiciels statistiques :

Comment calculer la corrélation point-bisériale dans Excel
Comment calculer la corrélation point-bisériale dans R
Comment calculer la corrélation point-bisériale en Python