Corrélation nulle

Cet article explique ce que signifie le fait que deux variables aient une corrélation nulle. Ainsi, vous trouverez un exemple résolu de variables aléatoires avec corrélation nulle et quelles sont les différences par rapport aux autres types de corrélation.

Qu’est-ce qu’une corrélation nulle ?

En statistiques, la corrélation nulle est un type de corrélation entre deux variables différentes. Plus précisément, lorsque deux variables ont une corrélation nulle, cela signifie qu’il n’y a aucune relation entre elles, c’est-à-dire qu’elles ne sont pas corrélées.

Mathématiquement, la corrélation nulle est identifiée car le coefficient de corrélation est égal à zéro. Cependant, si la valeur du coefficient de corrélation est très proche de 0, en général, on considère également qu’il y a une corrélation nulle puisque la corrélation est pratiquement inexistante.

Pour en savoir plus sur la corrélation, visitez le lien suivant :

Exemple de corrélation nulle

Après avoir vu la définition de la corrélation nulle, dans cette section, nous verrons un exemple de la vie quotidienne de deux variables qui ont une corrélation nulle.

• À partir d’un échantillon de 20 personnes différentes, leur taille et leur QI (utilisé pour mesurer l’intelligence d’une personne) ont été enregistrés dans le tableau de données suivant. Analysez la corrélation entre la taille et l’intelligence d’une personne.

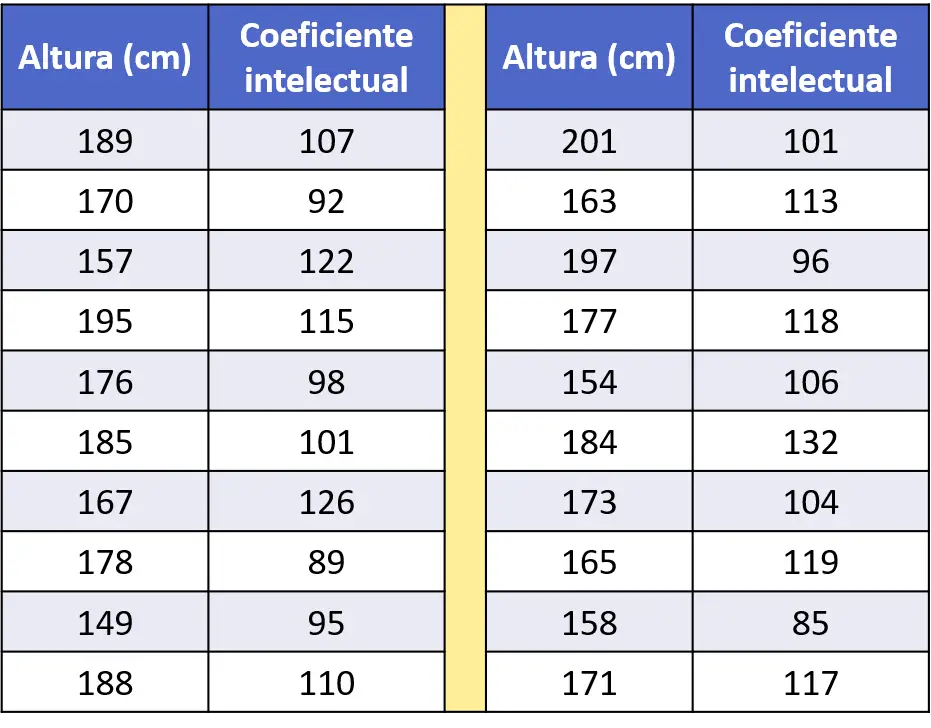
Tout d’abord, pour étudier la corrélation entre ces deux variables statistiques, nous devons représenter graphiquement les données, afin de savoir à quoi ressemble l’ensemble de données. Nous réalisons donc le nuage de points :

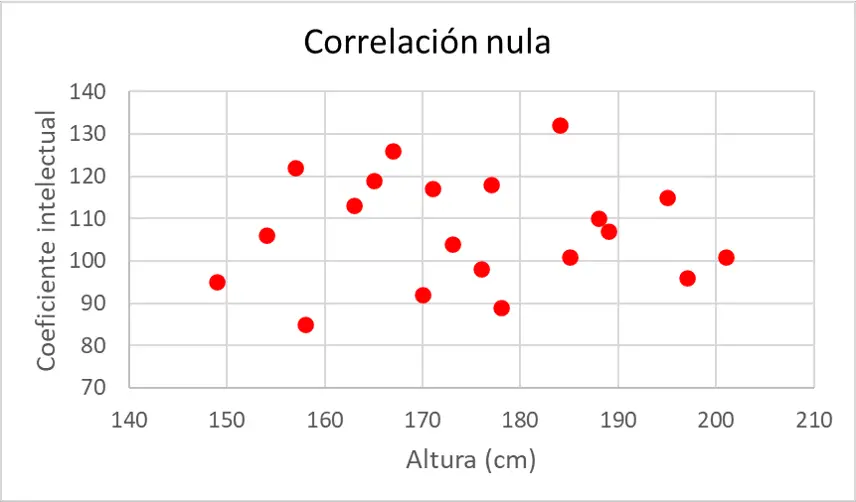
Après observation du graphique, aucune relation a priori n’est observée, puisque les points sont dispersés dans le diagramme sans suivre aucun motif.

Une fois que nous avons représenté graphiquement les données, nous calculons le coefficient de corrélation de Pearson, qui est un coefficient qui indique le degré de corrélation entre deux variables.

La valeur du coefficient de corrélation de Pearson est très proche de zéro, on conclut donc que la corrélation entre les deux variables d’exercice est nulle.

Gardez à l’esprit qu’il est très difficile que la valeur du coefficient de corrélation soit exactement nulle, vous devez donc interpréter le nombre obtenu avec le diagramme de dispersion et analyser si la corrélation entre les deux variables est nulle ou non.

Corrélation nulle, positive et nulle

Bien que cet article soit basé sur une corrélation nulle, sachez qu’il existe également deux autres types de corrélations : la corrélation positive et la corrélation négative. Ainsi, dans cette dernière section nous verrons la différence entre les types de corrélations.

• Corrélation positive – Une variable augmente lorsque l’autre augmente également. La valeur du coefficient de corrélation est comprise entre 0 (non inclus) et 1 (inclus).
• Corrélation négative : lorsqu’une variable augmente, l’autre diminue, et vice versa, si une variable diminue, l’autre augmente. La valeur du coefficient de corrélation est comprise entre -1 (inclus) et 0 (non inclus).
• Corrélation nulle : il n’y a aucune relation entre les deux variables. Le coefficient de corrélation est égal à 0.

Dans les graphiques suivants, vous pouvez voir représentés les différents types de corrélation :

Pour plus d’informations sur chaque type de corrélation, cliquez ici :