Correlation positive

Dans cet article, vous découvrirez ce que signifie une corrélation positive dans les statistiques, des exemples de variables avec une corrélation positive et quelles sont les différences entre d’autres types de corrélation.

Qu’est-ce qu’une corrélation positive ?

En statistiques, une corrélation positive est un type de corrélation entre deux variables différentes. Plus précisément, une corrélation positive entre deux variables signifie que si la valeur d’une variable augmente, l’autre variable augmente également.

Pour qu’une corrélation entre deux variables soit considérée comme positive, la valeur du coefficient de corrélation doit être comprise entre 0 (non inclus) et 1 (inclus).

Notez que la corrélation positive peut également être appelée corrélation directe .

Exemple de corrélation positive

Compte tenu de la définition de la corrélation positive, vous trouverez ci-dessous un exemple de deux variables présentant une corrélation de ce type.

• Dans le tableau de fréquence suivant, les notes en mathématiques et en statistiques d’un échantillon de 20 élèves ont été collectées sous forme de données. Analysez la relation entre les deux variables.

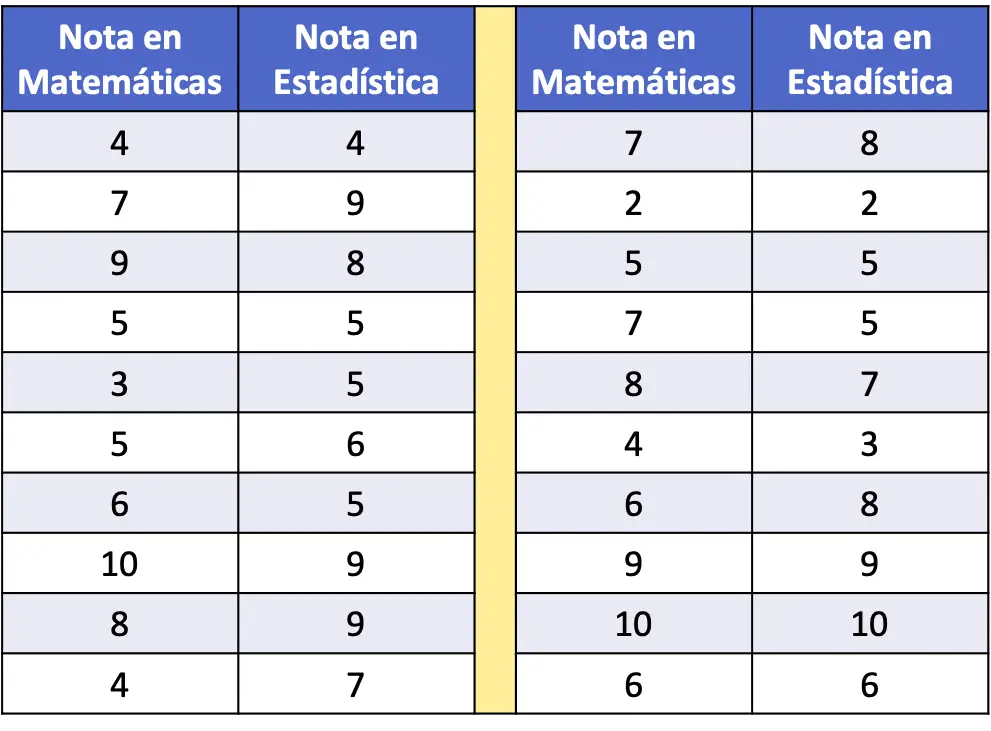
Avant de calculer le coefficient de corrélation, il est recommandé de représenter d’abord l’ensemble de données statistiques dans un nuage de points pour une exploration préliminaire.

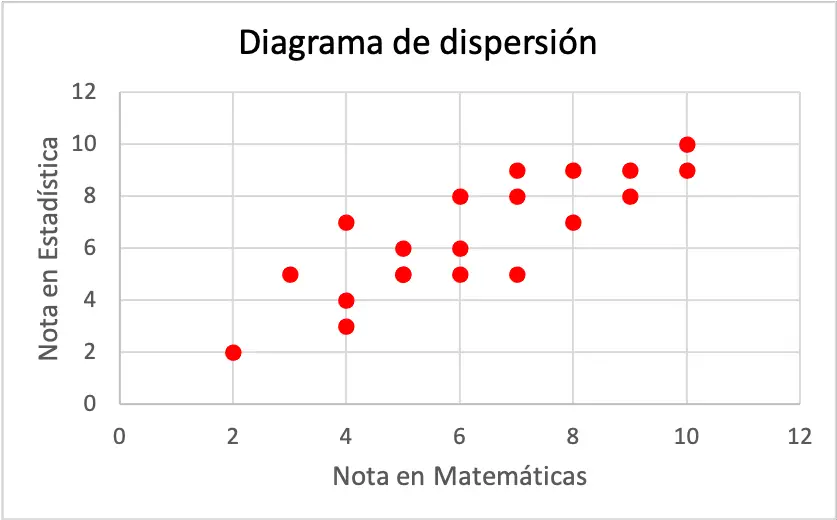
Comme le montre le graphique, il semble que les deux variables aient une corrélation linéaire positive, puisque lorsque la note en mathématiques augmente, la note en statistique augmente également. Mais pour déterminer avec certitude le type de corrélation il faut calculer le coefficient de corrélation :

La valeur du coefficient de corrélation de Pearson est supérieure à 0 et très proche de 1, la corrélation entre les deux variables étudiées est donc effectivement positive.

Interprétation de la corrélation positive

Pour finir de comprendre la signification de la corrélation positive en statistique, nous verrons dans cette section comment interpréter la valeur d’une corrélation positive entre deux variables.

Plus la valeur du coefficient de corrélation est élevée, plus les deux variables sont positivement corrélées. Ainsi, lorsque la valeur du coefficient de corrélation est proche de 1, cela signifie que la corrélation entre les deux variables est positive et très forte.

En revanche, lorsque la valeur du coefficient de corrélation est faible et proche de zéro, cela signifie que la corrélation entre les deux variables est positive mais faible. Même si le coefficient de corrélation devient nul ou négatif, cela implique que la corrélation est respectivement nulle ou négative. Nous verrons ci-dessous les différences entre ces trois types de corrélation.

Enfin, il convient de noter qu’une corrélation positive n’implique pas de causalité entre les variables. Autrement dit, si deux variables ont une corrélation positive, cela signifie qu’elles sont linéairement liées, mais qu’une variable n’est pas nécessairement la cause de l’autre.

À l’instar de la section précédente, les notes en mathématiques et en statistiques sont positivement corrélées, mais obtenir une bonne note en mathématiques ne garantit pas automatiquement une bonne note en statistiques, mais les deux matières doivent plutôt être étudiées. En conclusion, la note en mathématiques n’est pas la cause de la note en statistique, les deux variables sont simplement liées.

Corrélation positive, négative et nulle

Outre la corrélation positive, en statistique, deux variables peuvent également avoir une corrélation négative ou nulle. Par conséquent, dans cette section, nous verrons comment se distinguent ces trois types de corrélation.

• Corrélation positive : une variable augmente lorsque l’autre augmente également. La valeur du coefficient de corrélation est comprise entre 0 (non inclus) et 1 (inclus).
• Corrélation négative : lorsqu’une variable augmente, l’autre diminue, et vice versa, si une variable diminue, l’autre augmente. La valeur du coefficient de corrélation est comprise entre -1 (inclus) et 0 (non inclus).
• Corrélation nulle : il n’y a aucune relation entre les deux variables. Le coefficient de corrélation est égal à 0.

Dans les graphiques suivants, vous pouvez voir chaque type de corrélation représenté :