Corrélation vs régression : quelle est la différence ?

La corrélation et la régression sont deux termes statistiques liés, mais pas tout à fait identiques.

Dans ce didacticiel, nous fournirons une brève explication des deux termes et expliquerons en quoi ils sont similaires et différents.

Qu’est-ce que la corrélation ?

La corrélation mesure l’association linéaire entre deux variables, x et y . Il a une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Par exemple, supposons que nous ayons l’ensemble de données suivant qui contient deux variables : (1) Heures étudiées et (2) Résultats d’examen reçus pour 20 étudiants différents :

Si nous créions un nuage de points des heures étudiées par rapport aux résultats de l’examen, voici à quoi cela ressemblerait :

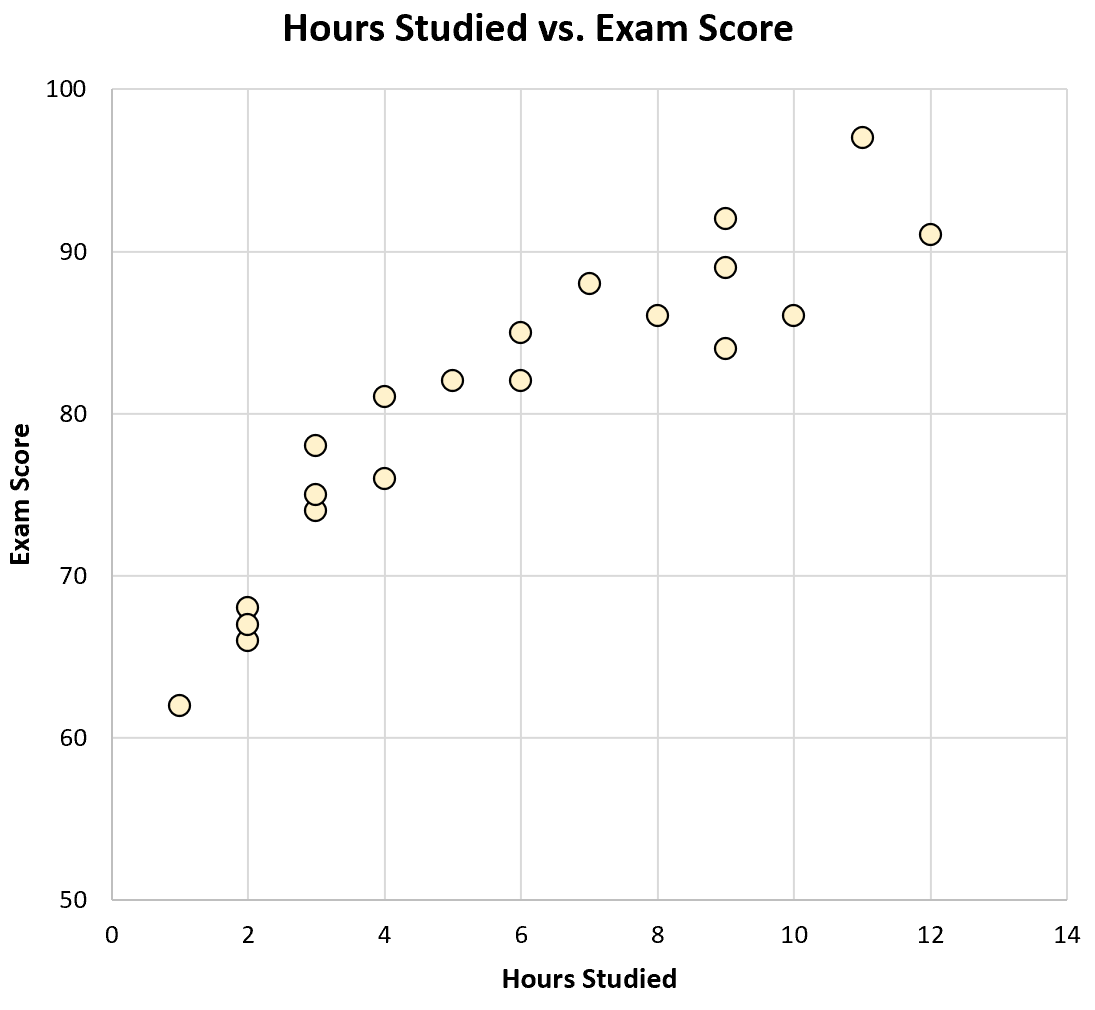
Rien qu’en regardant le graphique, nous pouvons constater que les étudiants qui étudient davantage ont tendance à obtenir de meilleurs résultats aux examens. En d’autres termes, nous pouvons voir visuellement qu’il existe une corrélation positive entre les deux variables.

À l’aide d’une calculatrice, nous pouvons constater que la corrélation entre ces deux variables est r = 0,915 . Cette valeur étant proche de 1, elle confirme qu’il existe une forte corrélation positive entre les deux variables.

Qu’est-ce que la régression ?

La régression est une méthode que nous pouvons utiliser pour comprendre comment la modification des valeurs de la variable x affecte les valeurs de la variable y .

Un modèle de régression utilise une variable, x , comme variable prédictive et l’autre variable, y , comme variable de réponse . Il trouve ensuite une équation de la forme suivante qui décrit le mieux la relation entre les deux variables :

ŷ = b ₀ + b ₁ x

où:

• ŷ : la valeur prédite de la variable de réponse
• b ₀ : L’ordonnée à l’origine (la valeur de y lorsque x est égal à zéro)
• b ₁ : Le coefficient de régression (l’augmentation moyenne de y pour une augmentation d’une unité de x)
• x : la valeur de la variable prédictive

Par exemple, considérons notre ensemble de données précédent :

À l’aide d’uncalculateur de régression linéaire , nous constatons que l’équation suivante décrit le mieux la relation entre ces deux variables :

Score prévu à l’examen = 65,47 + 2,58*(heures étudiées)

La façon d’interpréter cette équation est la suivante :

• La note prévue à l’examen pour un étudiant qui étudie zéro heure est de 65,47 .
• L’augmentation moyenne de la note à l’examen associée à une heure supplémentaire d’étude est de 2,58 .

Nous pouvons également utiliser cette équation pour prédire le score qu’un étudiant recevra en fonction du nombre d’heures étudiées.

Par exemple, un étudiant qui étudie 6 heures devrait recevoir une note de 80,95 :

Score prévu à l’examen = 65,47 + 2,58*(6) = 80,95 .

Nous pouvons également tracer cette équation sous forme de ligne sur un nuage de points :

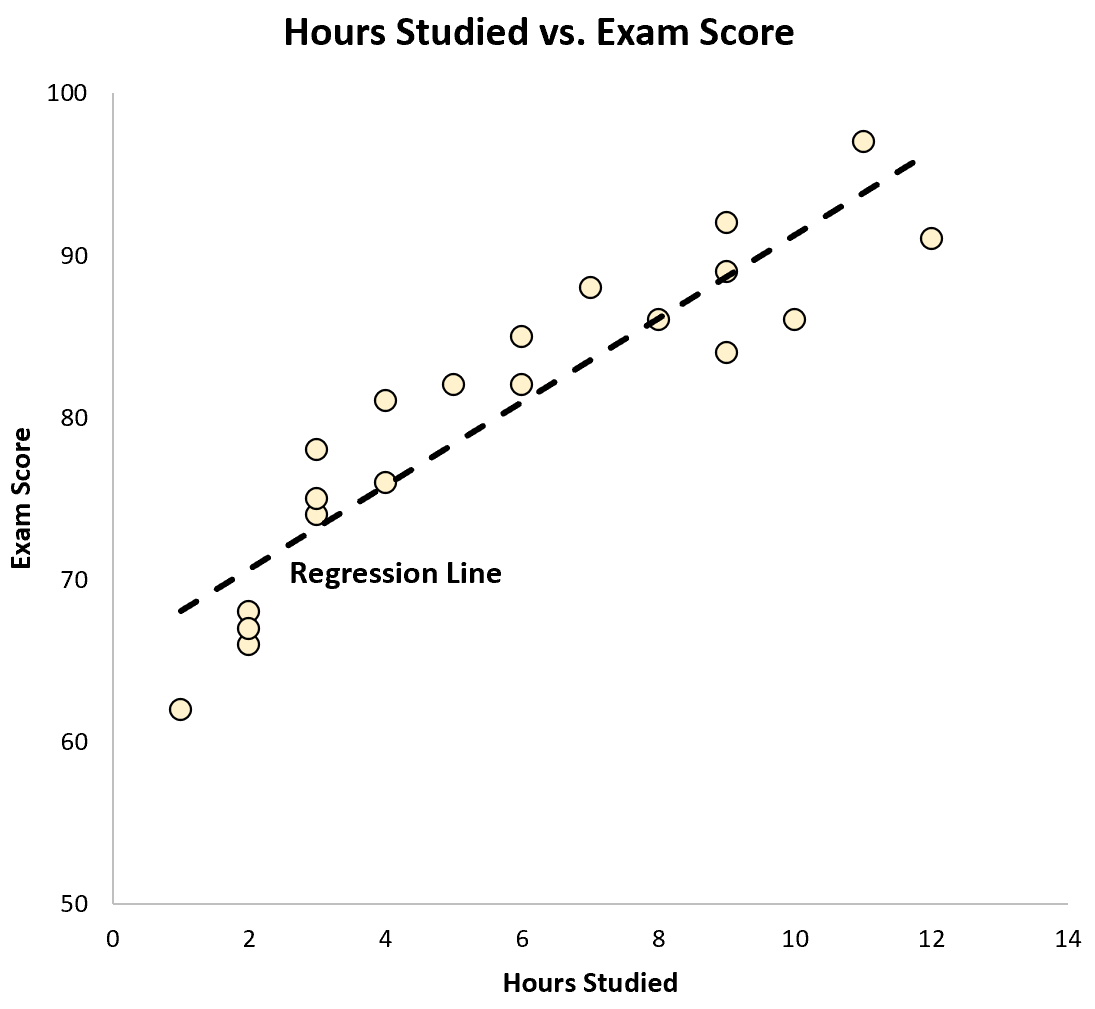
Nous pouvons voir que la droite de régression « correspond » assez bien aux données.

Rappelons plus tôt que la corrélation entre ces deux variables était r = 0,915 . Il s’avère que nous pouvons mettre cette valeur au carré et obtenir un nombre appelé « r au carré » qui décrit la proportion totale de variance dans la variable de réponse qui peut être expliquée par la variable prédictive.

Dans cet exemple, r ² = 0,915 ² = 0,837 . Cela signifie que 83,7 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées.

Corrélation vs régression : similarités et différences

Voici un résumé des similitudes et des différences entre corrélation et régression :

Similitudes:

• Les deux quantifient la direction d’une relation entre deux variables.
• Les deux quantifient la force d’une relation entre deux variables.

Différences:

• La régression est capable de montrer une relation de cause à effet entre deux variables. La corrélation ne fait pas cela.
• La régression est capable d’utiliser une équation pour prédire la valeur d’une variable, en fonction de la valeur d’une autre variable. La corrélation ne fait pas cela.
• La régression utilise une équation pour quantifier la relation entre deux variables. La corrélation utilise un seul nombre.

Ressources additionnelles

Les didacticiels suivants offrent des explications plus approfondies des sujets abordés dans cet article.

Une introduction au coefficient de corrélation de Pearson
Une introduction à la régression linéaire simple
Calculateur de régression linéaire simple
Qu’est-ce qu’une bonne valeur R au carré ?