Corrélations dans Stata : Pearson, Spearman et Kendall
En statistique, la corrélation fait référence à la force et à la direction d’une relation entre deux variables. La valeur d’un coefficient de corrélation peut aller de -1 à 1, -1 indiquant une relation négative parfaite, 0 indiquant l’absence de relation et 1 indiquant une relation positive parfaite.
Il existe trois manières courantes de mesurer la corrélation :
Corrélation de Pearson : utilisée pour mesurer la corrélation entre deux variables continues. (par exemple taille et poids)
Corrélation de Spearman : utilisée pour mesurer la corrélation entre deux variables classées. (par exemple, classement de la note à l’examen de mathématiques d’un élève par rapport au classement de sa note à l’examen de sciences dans une classe)
Corrélation de Kendall : utilisée lorsque vous souhaitez utiliser la corrélation de Spearman mais que la taille de l’échantillon est petite et qu’il existe de nombreux classements liés.
Ce tutoriel explique comment trouver les trois types de corrélations dans Stata.
Chargement des données
Pour chacun des exemples suivants, nous utiliserons un ensemble de données appelé auto . Vous pouvez charger cet ensemble de données en tapant ce qui suit dans la zone Commande :
utilisez https://www.stata-press.com/data/r13/auto
Nous pouvons avoir un aperçu rapide de l’ensemble de données en tapant ce qui suit dans la zone de commande :
résumer
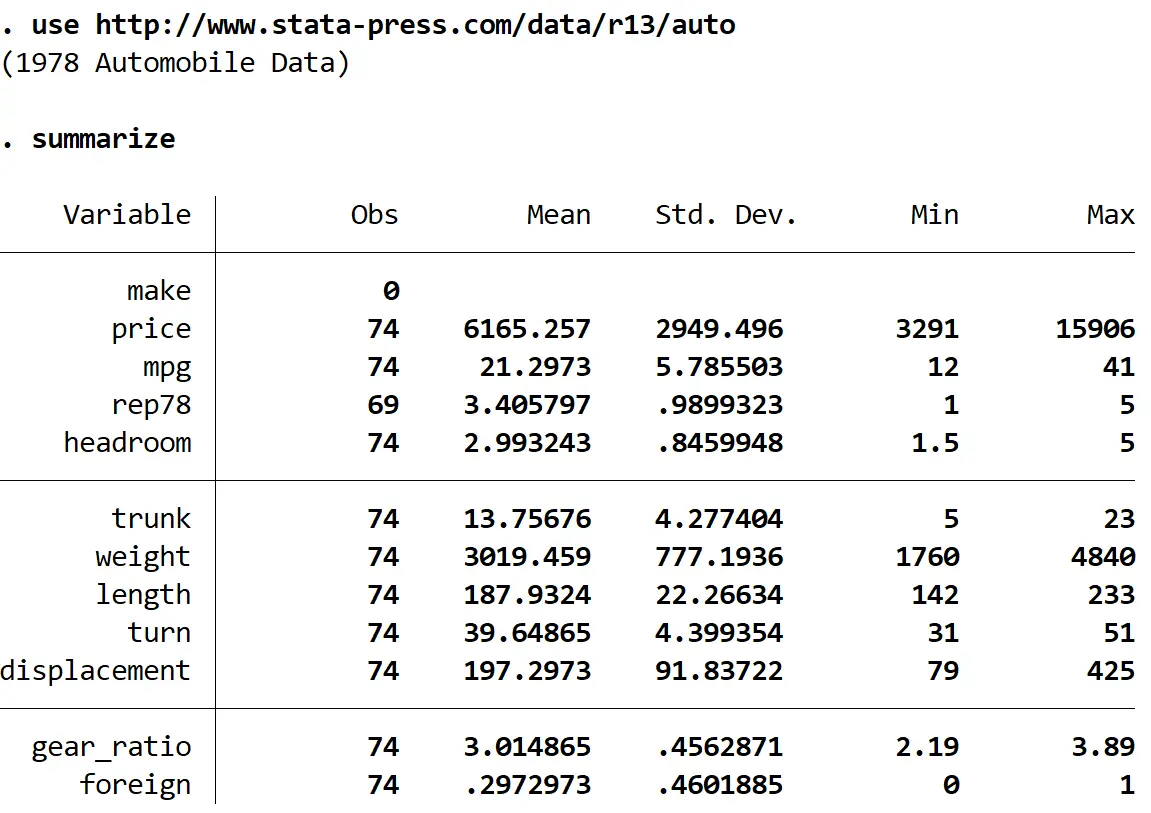
Nous pouvons voir qu’il y a 12 variables au total dans l’ensemble de données.
Comment trouver la corrélation de Pearson dans Stata
Nous pouvons trouver le coefficient de corrélation de Pearson entre les variables poids et longueur en utilisant la commande pwcorr :
pwcorr poids longueur
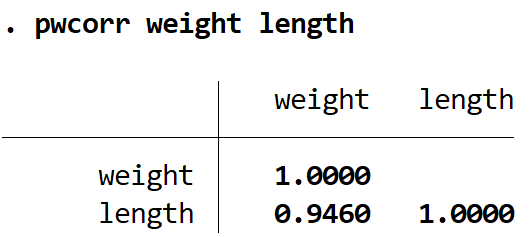
Le coefficient de corrélation de Pearson entre ces deux variables est de 0,9460 . Pour déterminer si ce coefficient de corrélation est significatif, nous pouvons trouver la valeur de p en utilisant la commande sig :
pwcorr poids longueur, sig
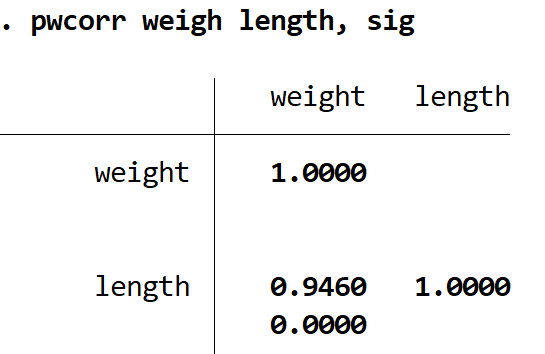
La valeur p est de 0,000 . Comme celle-ci est inférieure à 0,05, la corrélation entre ces deux variables est statistiquement significative.
Pour trouver le coefficient de corrélation de Pearson pour plusieurs variables, tapez simplement une liste de variables après la commande pwcorr :
pwcorr poids longueur déplacement, sig
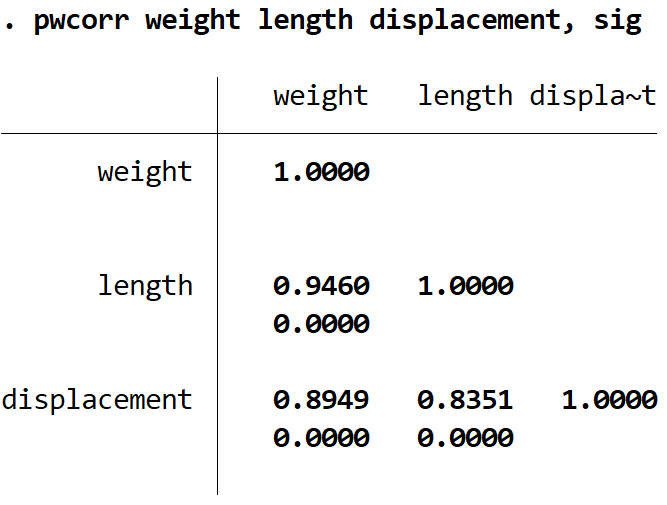
Voici comment interpréter le résultat :
- Corrélation de Pearson entre le poids et la longueur = 0,9460 | valeur p = 0,000
- Corrélation de Pearson entre le poids et le déplacement = 0,8949 | valeur p = 0,000
- Corrélation de Pearson entre le déplacement et la longueur = 0,8351 | valeur p = 0,000
Comment trouver la corrélation de Spearman dans Stata
Nous pouvons trouver le coefficient de corrélation de Spearman entre les variables trunk et rep78 en utilisant la commande spearman :
tronc de lancier rep78

Voici comment interpréter le résultat :
- Nombre d’obs : Il s’agit du nombre d’observations par paires utilisées pour calculer le coefficient de corrélation de Spearman. Comme il manquait certaines valeurs pour la variable rep78 , Stata n’a utilisé que 69 observations par paire (au lieu des 74 au complet).
- Rho de Spearman : C’est le coefficient de corrélation de Spearman. Dans ce cas, il s’agit de -0,2235, ce qui indique qu’il existe une corrélation négative entre les deux variables. À mesure que l’un augmente, l’autre tend à diminuer.
- Prob > |t| : Il s’agit de la valeur p associée au test d’hypothèse. Dans ce cas, la valeur p est de 0,0649, ce qui indique qu’il n’existe pas de corrélation statistiquement significative entre les deux variables à α = 0,05.
Nous pouvons trouver le coefficient de corrélation de Spearman pour plusieurs variables en tapant simplement plus de variables après la commande spearman . Nous pouvons trouver le coefficient de corrélation et la valeur p correspondante pour chaque corrélation par paire en utilisant la commande stats(rho p) :
spearman trunk rep78 gear_ratio, stats (rho p)

Voici comment interpréter le résultat :
- Corrélation de Spearman entre le tronc et le rep78 = -0,2235 | valeur p = 0,0649
- Corrélation de Spearman entre le tronc et le ratio_engrenage = -0,5187 | valeur p = 0,0000
- Corrélation de Spearman entre gear_ratio et rep78 = 0,4275 | valeur p = 0,0002
Comment trouver la corrélation de Kendall dans Stata
Nous pouvons trouver le coefficient de corrélation de Kendall entre les variables trunk et rep78 en utilisant la commande ktau :
ktau tronc rep78

Voici comment interpréter le résultat :
- Nombre d’obs : Il s’agit du nombre d’observations par paires utilisées pour calculer le coefficient de corrélation de Kendall. Comme il manquait certaines valeurs pour la variable rep78 , Stata n’a utilisé que 69 observations par paire (au lieu des 74 au complet).
- Tau-b de Kendall : Il s’agit du coefficient de corrélation de Kendall entre les deux variables. Nous utilisons généralement cette valeur au lieu de tau-a car tau-b effectue des ajustements en cas d’égalité. Dans ce cas, tau-b = -0,1752, indiquant une corrélation négative entre les deux variables.
- Prob > |z| : Il s’agit de la valeur p associée au test d’hypothèse. Dans ce cas, la valeur p est de 0,0662, ce qui indique qu’il n’existe pas de corrélation statistiquement significative entre les deux variables à α = 0,05.
Nous pouvons trouver le coefficient de corrélation de Kendall pour plusieurs variables en tapant simplement plus de variables après la commande ktau . Nous pouvons trouver le coefficient de corrélation et la valeur p correspondante pour chaque corrélation par paire en utilisant la commande stats(taub p) :
ktau trunk rep78 gear_ratio, stats (taub p)
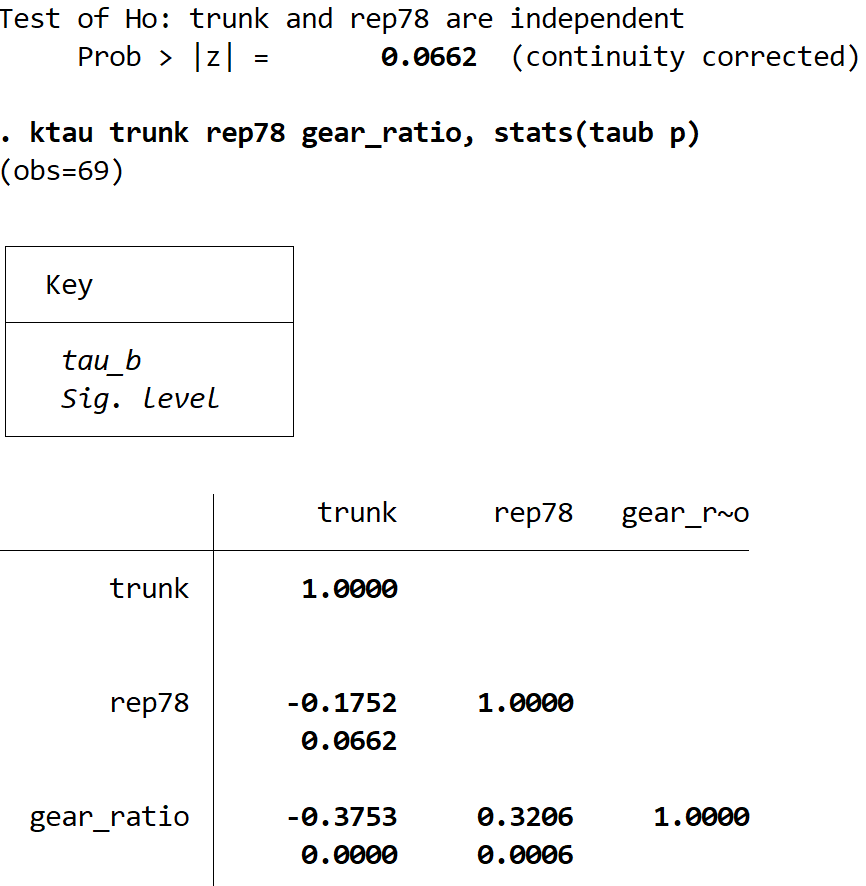
- Corrélation de Kendall entre le tronc et le rep78 = -0,1752 | valeur p = 0,0662
- Corrélation de Kendall entre le tronc et le ratio_engrenage = -0,3753 | valeur p = 0,0000
- Corrélation de Kendall entre gear_ratio et rep78 = 0,3206 | valeur p = 0,0006
