Courbe de Lorenz

Cet article explique ce qu’est la courbe de Lorenz et à quoi elle sert. Vous découvrirez comment réaliser la courbe de Lorenz d’une population et, en plus, vous pourrez voir l’exercice résolu étape par étape. Enfin, les propriétés de la courbe de Lorenz et la relation avec l’indice de Gini sont présentées.

Qu’est-ce que la courbe de Lorenz ?

La courbe de Lorenz est la représentation graphique des inégalités économiques de la population d’un territoire. Autrement dit, la courbe de Lorenz est une courbe qui permet d’analyser les inégalités dans la répartition des revenus sur un territoire.

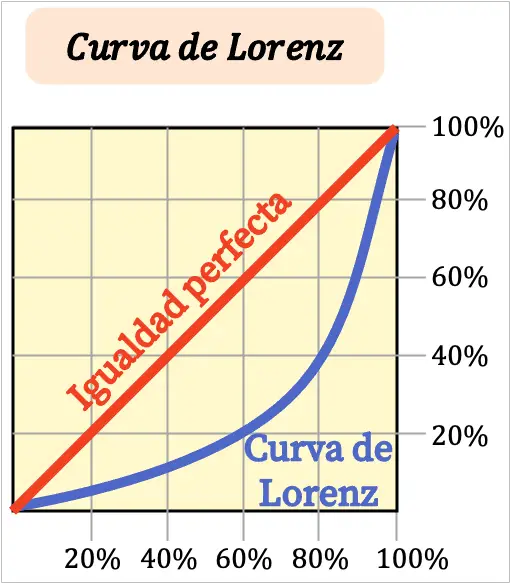
Plus la courbe de Lorenz est droite, plus les revenus du territoire sont égalitaires. En revanche, plus la courbe de Lorenz est courbée, plus les revenus sont répartis de manière inégale.

En général, les axes de la courbe de Lorenz sont exprimés en pourcentage. L’axe X du graphique représente le pourcentage de la population et, d’autre part, l’axe Y indique le pourcentage de revenu.

La courbe de Lorenz a été inventée en 1905 par Max Otto Lorenz, un économiste américain très important du XXe siècle.

Comment calculer la courbe de Lorenz

Une fois que nous connaîtrons la définition de la courbe de Lorenz, nous verrons ensuite comment cette courbe statistique est calculée. Il est à noter qu’il existe une formule pour définir la courbe de Lorenz, mais en pratique elle n’est généralement pas utilisée. C’est pourquoi nous allons résoudre un exemple étape par étape afin que vous puissiez voir comment cela se fait.

• Représente la courbe de Lorenz de la population dont les revenus sont présentés dans le tableau suivant :

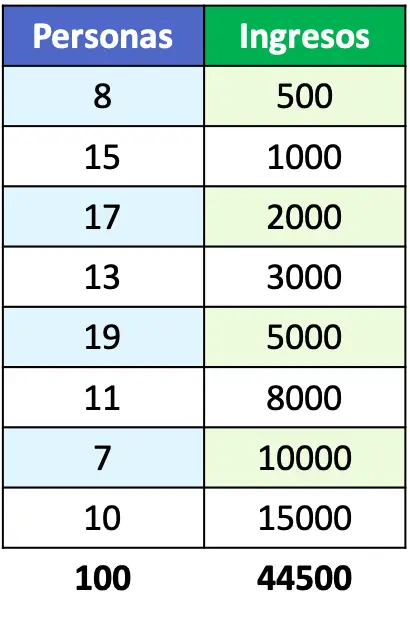
Si l’énoncé du problème nous donnait l’exemple de fonction de courbe de Lorenz, nous pourrions représenter directement la fonction sur un graphique. Mais dans ce cas, ils nous donnent uniquement le revenu de la population, nous devons donc calculer le pourcentage de chaque groupe de personnes.

Ainsi, pour déterminer les pourcentages du nombre de personnes et du revenu, nous devons ajouter deux colonnes au tableau pour la variable population :

• Une colonne avec la fréquence absolue accumulée (F _i ).
• Une deuxième colonne qui correspond au pourcentage cumulé, qui est calculé en divisant la fréquence absolue cumulée par le nombre total de personnes.

Et, d’autre part, il faut ajouter trois colonnes pour la variable revenu :

• Colonne dans laquelle est calculé le revenu total, équivalent au produit du nombre de personnes par le revenu que chaque personne reçoit.
• Une seconde avec la fréquence absolue accumulée (F _i ) du revenu total.
• Une troisième colonne qui comprend le pourcentage accumulé, déterminé en divisant la colonne précédente par le revenu total de la population.

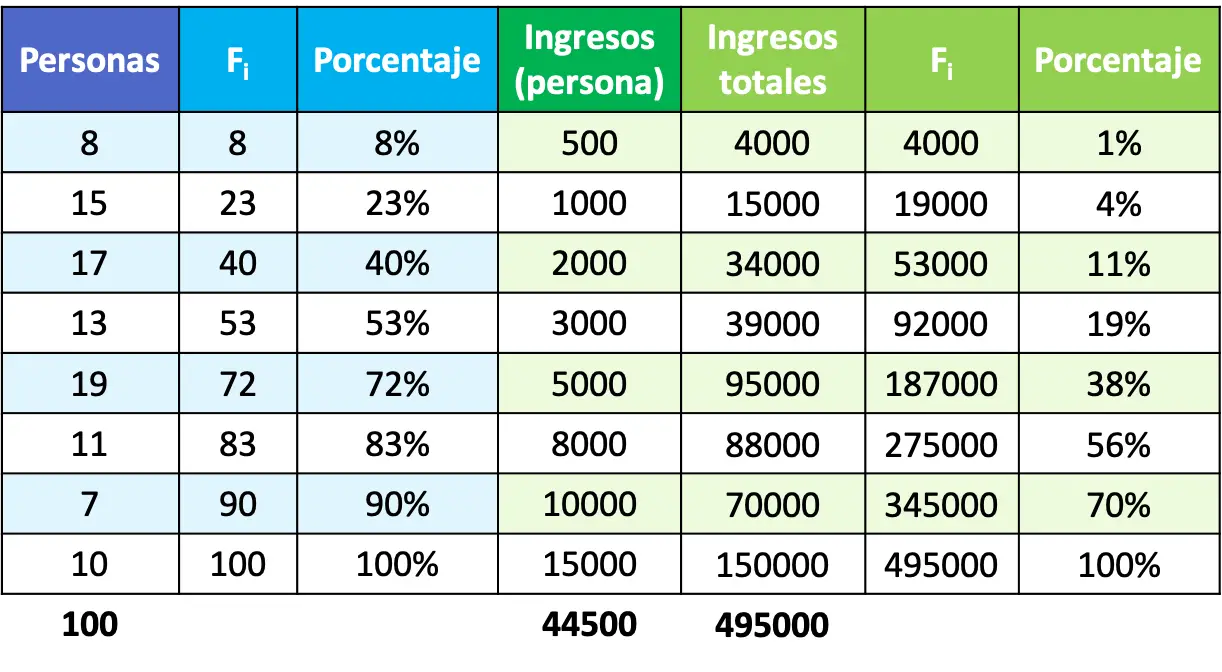
Enfin, maintenant que nous avons calculé les pourcentages, il ne reste plus qu’à tracer les points sur un graphique et à les joindre pour former la courbe de Lorenz. N’oubliez pas que l’axe X est le pourcentage de la population et l’axe Y est le pourcentage du revenu.

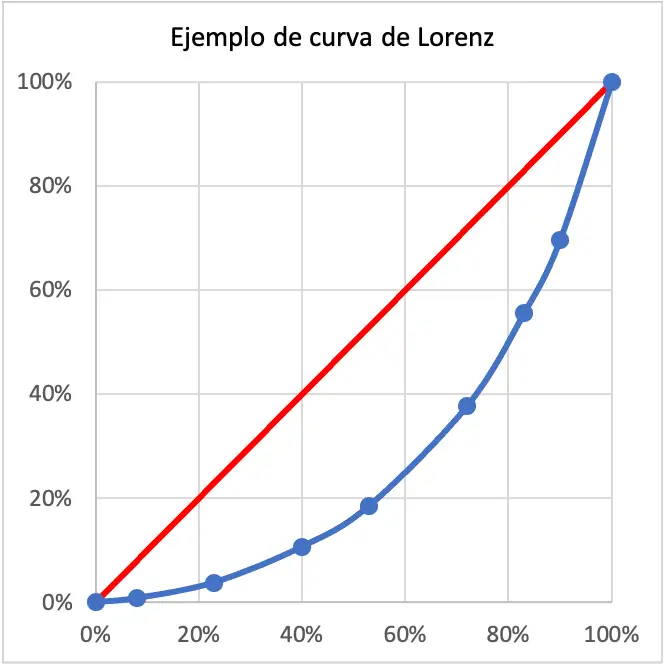
Dans ce cas, les revenus de la population étudiée sont très inégaux, puisque la courbe de Lorenz est très large. En fait, la courbe de Lorenz est très éloignée de la ligne rouge qui représente l’égalité parfaite.

Interprétation de la courbe de Lorenz

Cette section explique comment interpréter la courbe de Lorenz d’une population, car en plus de savoir la représenter graphiquement, vous devez comprendre ce qu’elle signifie.

La courbe de Lorenz indique quel pourcentage de la population détient un pourcentage du revenu total d’un territoire. Par exemple, dans l’exemple de courbe de Lorenz illustré ci-dessus, 40 % de la population a un revenu qui correspond à 11 % de tous les revenus de la population. C’est donc un territoire très inégal.

Ainsi, la courbe de Lorenz représente visuellement l’égalité ou l’inégalité des revenus entre les habitants d’un pays ou d’un territoire. Plus on s’éloigne de la ligne indiquant l’égalité parfaite, plus cela signifie que les revenus de la population sont plus inégaux. En revanche, plus la courbe de Lorenz se rapproche de la droite, plus elle implique que les revenus de la population sont répartis plus équitablement.

De plus, si une courbe de Lorenz est au-dessus d’une autre courbe de Lorenz tout au long du graphique, cela signifie que le revenu de la première population est plus égal que celui de la seconde.

Courbe de Lorenz et coefficient de Gini

Comme expliqué tout au long de l’article, la courbe de Lorenz montre graphiquement comment les revenus d’un territoire sont répartis et à quel point un territoire est inégal.

D’autre part, le coefficient de Gini, également appelé indice de Gini, indique numériquement l’inégalité économique d’un territoire.

La courbe de Lorenz et le coefficient de Gini sont donc liés. En effet, le coefficient de Gini d’un pays peut être calculé à partir de sa courbe de Lorenz. Dans l’article suivant, vous pouvez voir comment procéder :

Propriétés de la courbe de Lorenz

La courbe de Lorenz a les propriétés suivantes :

• La courbe de Lorenz commence toujours au point (0,0) et se termine à (100,100).
• La courbe de Lorenz n’est pas définie si la moyenne de l’échantillon est égale à zéro.
• La courbe de Lorenz ne peut pas figurer sur le graphique au-dessus de la ligne d’égalité parfaite.
• En supposant que le revenu ne peut pas être négatif, la courbe de Lorenz est toujours croissante.