Que sont les courbes de densité ? (Explication & Exemples)

Une courbe de densité est une courbe sur un graphique qui représente la distribution des valeurs dans un ensemble de données. C’est utile pour trois raisons :

1. Une courbe de densité nous donne une bonne idée de la « forme » d’une distribution, notamment si une distribution présente ou non un ou plusieurs « pics » de valeurs fréquentes et si la distribution est asymétrique ou non vers la gauche ou la droite. .

2. Une courbe de densité nous permet de voir visuellement où se situent la moyenne et la médiane d’une distribution.

3. Une courbe de densité nous permet de voir visuellement quel pourcentage d’observations dans un ensemble de données se situe entre différentes valeurs.

La courbe de densité la plus connue est la courbe en forme de cloche qui représente ladistribution normale .

Pour mieux comprendre les courbes de densité, considérons l’exemple suivant.

Exemple : création et interprétation d’une courbe de densité

Supposons que nous ayons l’ensemble de données suivant qui montre la hauteur de 20 plantes différentes (en pouces) dans un certain champ :

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Si nous créions un histogramme simple pour afficher les fréquences relatives de chaque valeur, cela ressemblerait à ceci :

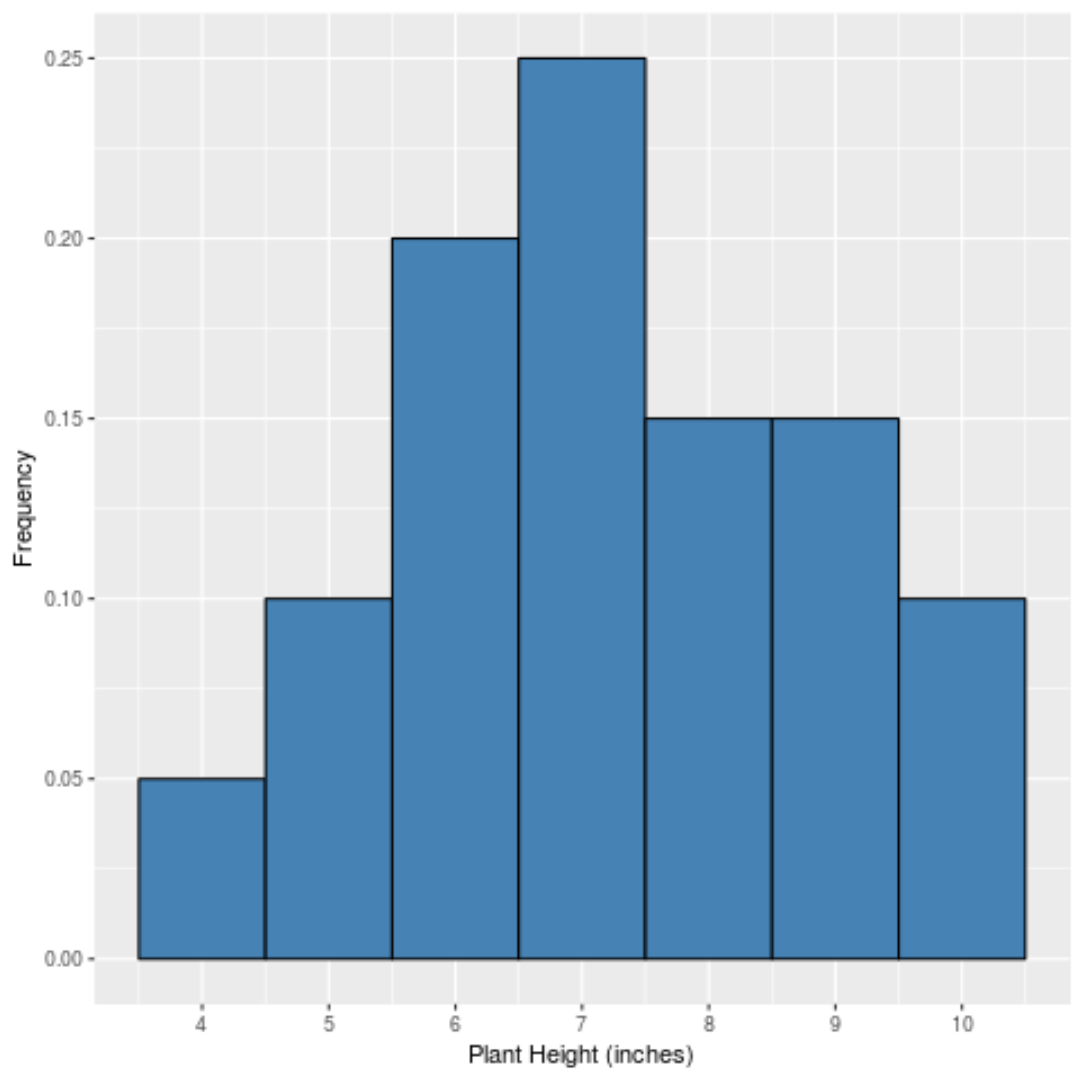
L’axe des x montre la valeur des données et l’axe des y montre la fréquence relative (par exemple, la valeur « 7 » apparaît 5 fois sur 20 valeurs totales dans l’ensemble de données, elle a donc une fréquence relative de 25 % ou 0,25 .

Et si nous créions une courbe de densité pour capturer la « forme » de cette distribution, elle ressemblerait à ceci :

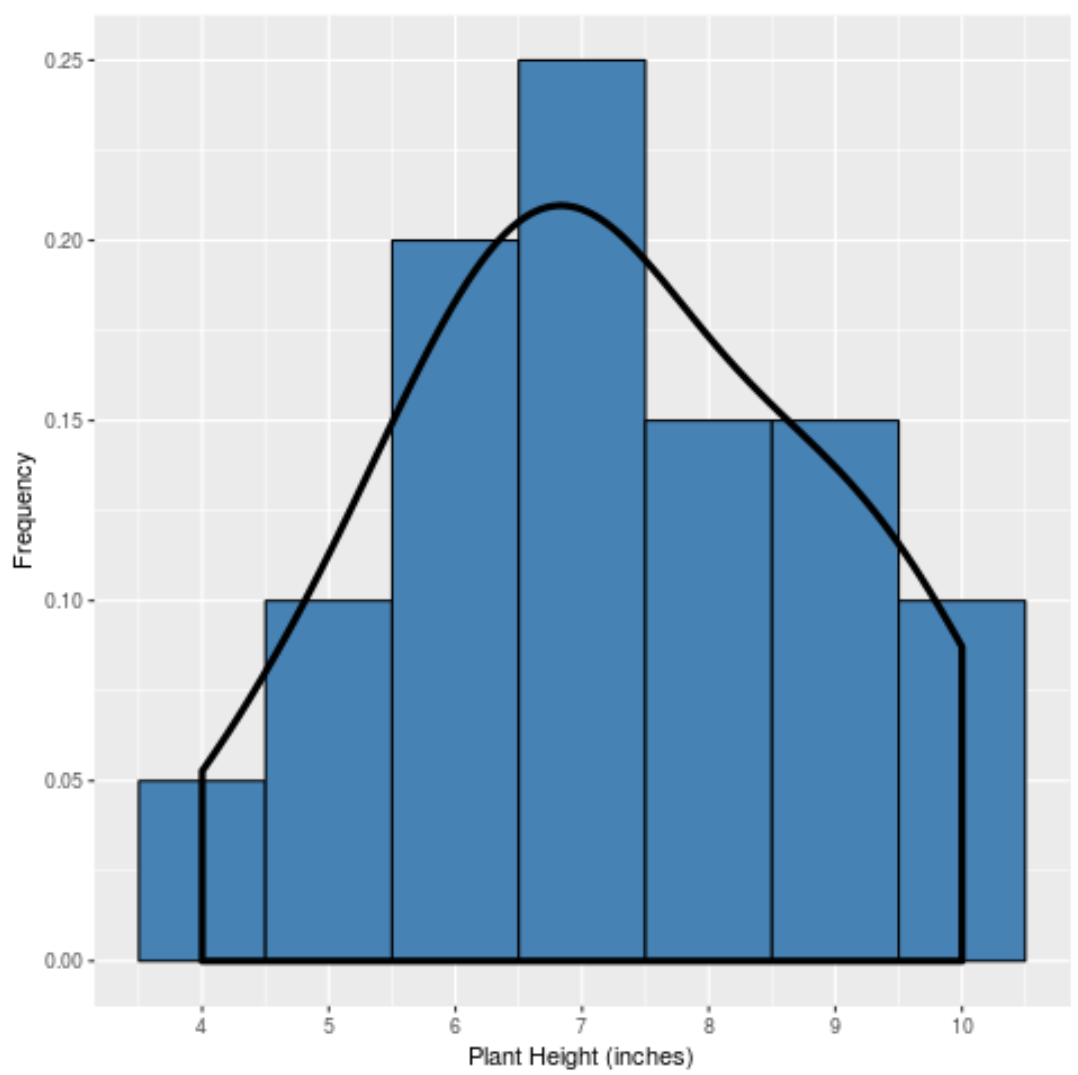
La courbe est la plus élevée près du centre de la distribution car c’est là que se trouvent la plupart des valeurs. Il est également le plus bas près des extrémités de la distribution car moins de plantes prennent ces valeurs (par exemple une hauteur de 4 pouces ou 10 pouces).

Comment interpréter les courbes de densité

Les courbes de densité sont de toutes formes et tailles et elles nous permettent d’acquérir une compréhension visuelle rapide de la distribution des valeurs dans un ensemble de données donné. Ils sont notamment utiles pour nous aider à visualiser :

1. Asymétrie

L’asymétrie est une façon de décrire la symétrie d’une distribution. Les courbes de densité nous permettent de voir rapidement si un graphique est incliné à gauche, à droite ou n’a pas d’inclinaison :

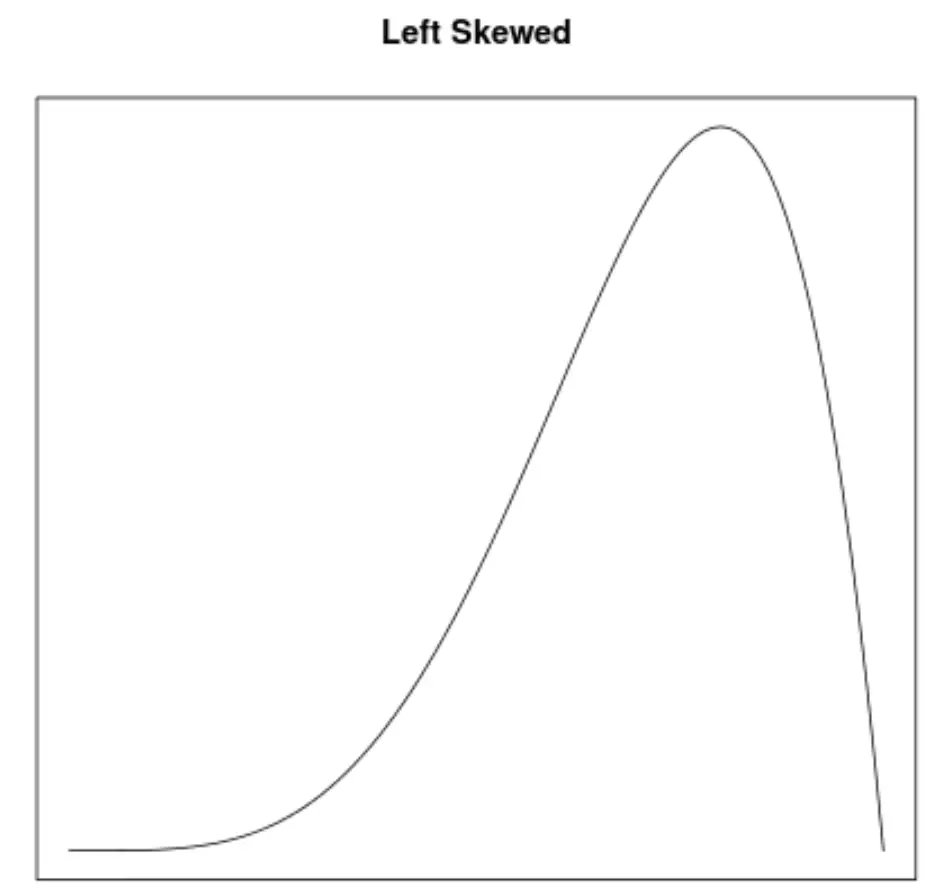
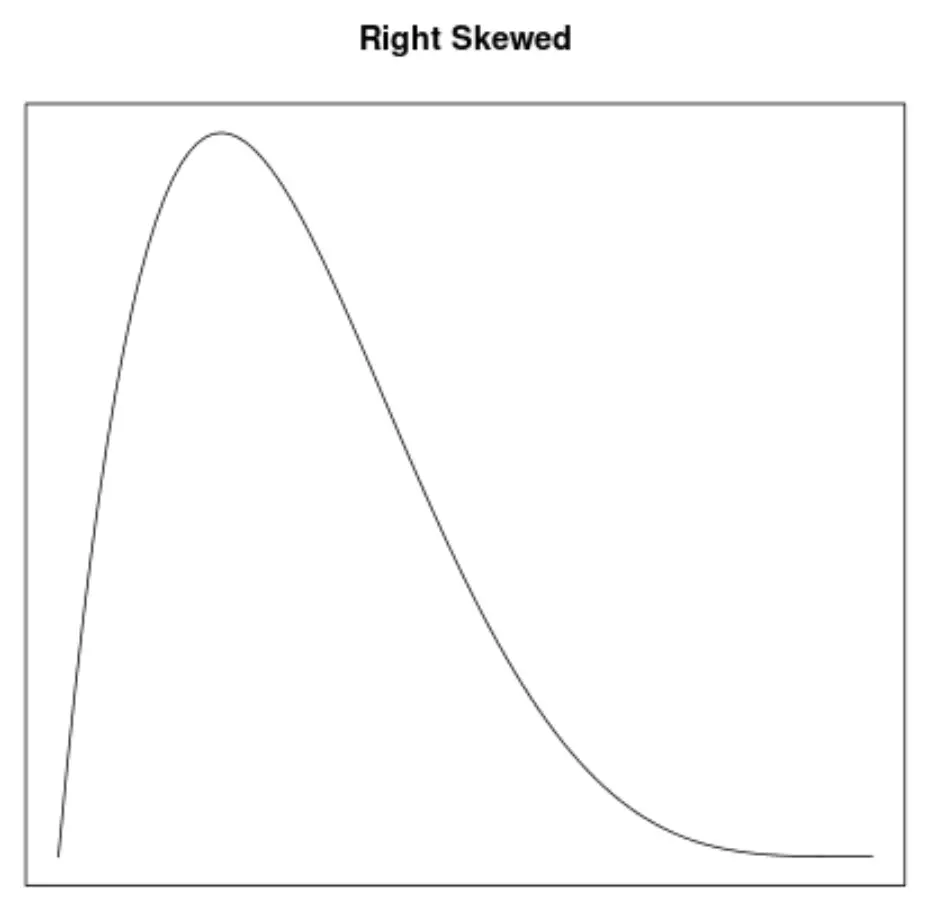
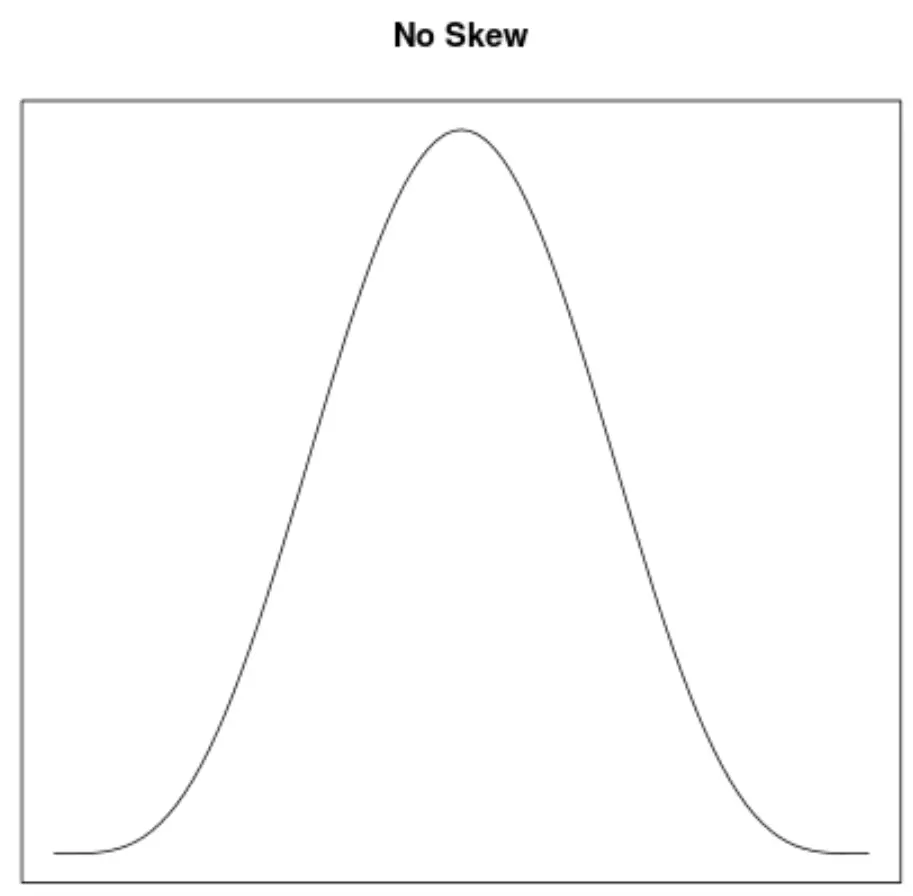
2. L’emplacement de la moyenne et de la médiane

En fonction de l’asymétrie d’une courbe de densité, nous pouvons rapidement savoir si la moyenne ou la médiane est plus grande dans une distribution donnée. En particulier:

• Si une courbe de densité reste asymétrique , alors la moyenne est inférieure à la médiane.
• Si une courbe de densité est asymétrique à droite , alors la moyenne est supérieure à la médiane.
• Si une courbe de densité n’a pas d’asymétrie , alors la moyenne est égale à la médiane.

3. Nombre de pics

Les courbes de densité nous permettent également de voir rapidement combien de « pics » il y a dans une distribution donnée. Dans chacun des exemples ci-dessus, les distributions n’avaient qu’un seul pic, nous décririons donc ces distributions comme unimodales .

Cependant, certaines distributions peuvent avoir deux pics que nous appelons distributions bimodales . Et dans de rares cas, nous pouvons également avoir des distributions multimodales comportant deux pics ou plus.

En créant simplement une courbe de densité pour un ensemble de données donné, nous pouvons rapidement voir combien de pics se trouvent dans la distribution.

Propriétés des courbes de densité

Les courbes de densité ont les propriétés suivantes :

• L’aire sous la courbe totalise toujours 100 %.
• La courbe ne descendra jamais en dessous de l’axe des x.

Gardez ces deux faits à l’esprit lorsque vous créez ou interprétez des courbes de densité pour différentes distributions.

Ressources additionnelles

Introduction aux histogrammes de fréquence relative
Comment créer une courbe en cloche dans Excel
Comment créer une courbe en cloche en Python