Covariance

Par Pr Amélia Rodriguez août 5, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est la covariance et comment elle est calculée. Vous trouverez la formule de covariance ainsi qu’un exemple de calcul de la covariance d’un ensemble de données. De plus, vous pouvez calculer la covariance de n’importe quelle série de données avec le calculateur en ligne à la fin.

Qu’est-ce que la covariance ?

En statistique, la covariance est une valeur qui indique le degré de variation conjointe de deux variables aléatoires. Autrement dit, la covariance est utilisée pour analyser la dépendance entre deux variables.

La covariance est égale à la somme des produits des différences entre les données des deux variables et leurs moyennes respectives divisée par le nombre total de données.

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la covariance de n’importe quel ensemble de données.

L’interprétation de la valeur de covariance est très simple :

Si la covariance est positive , cela signifie qu’il existe une dépendance entre les deux variables. Par conséquent, lorsqu’une variable augmente en valeur, l’autre variable augmente également, et vice versa.
Si la covariance est négative , cela signifie que la relation entre les deux variables est négative. Ainsi, lorsqu’une variable augmente en valeur, l’autre variable diminue, et vice versa.
Si la covariance est égale à zéro (ou si sa valeur est proche de zéro), cela implique qu’il n’y a aucune relation entre les deux variables. Autrement dit, les deux variables aléatoires sont indépendantes.

Comment calculer la covariance

Pour calculer la covariance d’une série de données, les étapes suivantes doivent être effectuées :

Calculez la moyenne de chaque variable séparément.
Pour chaque variable, trouvez la différence entre chacune de ses valeurs et la moyenne de la variable.
Multipliez les différences calculées à l’étape précédente pour chaque donnée.
Additionnez tous les résultats obtenus à l’étape précédente.
Divisez par le nombre total de données. La valeur obtenue est la covariance de la série de données.

En résumé, la formule pour calculer la covariance entre deux variables est la suivante :

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

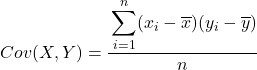
Une méthode fortement recommandée pour extraire la covariance entre deux variables consiste à créer un tableau avec toutes les paires de données et à ajouter une colonne pour chacune des étapes expliquées ci-dessus. De cette façon, vos calculs seront bien mieux organisés et vous comprendrez mieux ce que vous faites.

Exemple de calcul de covariance

Compte tenu de la définition de la covariance, vous trouverez ci-dessous un exemple étape par étape du calcul de ce type de mesure statistique. L’objectif est que vous compreniez mieux la notion de covariance et comment analyser la corrélation entre deux variables.

Calculez la covariance de l’ensemble de données statistiques suivant :

Tout d’abord, nous devons calculer la moyenne arithmétique de chaque variable. Pour ce faire, on divise la somme des valeurs de chaque variable par le nombre total de données.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Voir : formule de moyenne arithmétique

Une fois que nous avons déterminé la moyenne de chaque variable aléatoire, nous pouvons ajouter les colonnes suivantes au tableau de données pour obtenir la covariance :

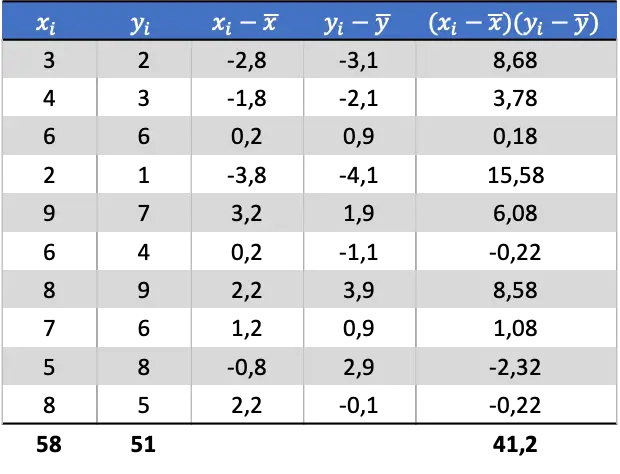
Donc pour déterminer la covariance des deux variables il faut diviser la somme de la dernière colonne par le nombre de paires de données :

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

Dans ce cas la valeur de covariance est positive, ce qui signifie qu’il existe une dépendance directe entre les deux variables aléatoires étudiées. Cependant, si la valeur de covariance avait été négative, cela signifierait que la dépendance entre les deux variables est inverse. Et enfin, si la valeur de covariance est nulle ou très proche de zéro, cela signifie qu’il n’y a pas de relation linéaire entre les deux variables.

Comme vous pouvez le voir dans la résolution de cet exemple, il est très utile d’utiliser un programme informatique tel qu’Excel pour ajouter les colonnes au tableau et effectuer les calculs rapidement. Sinon, en calculant les opérations manuellement, il faut beaucoup plus de temps pour trouver la covariance.

Calculateur de covariance

Entrez un ensemble de données statistiques dans la calculatrice suivante pour calculer la covariance entre deux variables. Vous devez séparer les paires de données, de sorte que dans la première case il n’y ait que les valeurs d’une variable et dans la deuxième case il n’y ait que les valeurs de la deuxième variable.

Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Propriétés de covariance

La covariance a les propriétés suivantes :

La covariance entre une variable aléatoire et une constante est nulle.

$Cov(X,a)=0$

La covariance d’une variable et elle-même est équivalente à la variance de cette variable.

$Cov(X,X)=Var(X)$

➤ Voir : qu’est-ce que la variance ?

La covariance satisfait la propriété de symétrie, donc la covariance des variables X et Y est égale à la covariance des variables Y et X. L’ordre des variables n’affecte pas le résultat de la covariance.

$Cov(X,Y)=Cov(Y,X)$

Si les variables sont multipliées par des constantes, vous pouvez d’abord calculer la covariance puis multiplier le résultat par les constantes.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

L’ajout de termes aux variables n’affecte pas le résultat de la covariance.

$Cov(a+X,b+Y)=Cov(X+Y)$

La covariance entre deux variables aléatoires est liée à leurs attentes mathématiques. La covariance entre les variables X et Y est égale à l’espérance mathématique du produit de X et Y moins le produit de l’espérance mathématique de chaque variable.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

Lors d’opérations avec des variables, l’expression algébrique suivante est remplie par rapport à la covariance :

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus