Critère de Chauvenet : Définition & Exemple
Une valeur aberrante est une observation anormalement éloignée des autres valeurs d’un ensemble de données. Les valeurs aberrantes peuvent poser problème car elles peuvent affecter les résultats d’une analyse.
Une façon d’identifier les valeurs aberrantes dans un ensemble de données consiste à utiliser le critère de Chauvenet , qui utilise le processus suivant :
1. Pour chaque valeur individuelle x i dans l’ensemble de données, calculez l’écart par rapport à la moyenne comme suit :
Déviation = |x je – x | /s
où x est la moyenne de l’échantillon et s est l’écart type de l’échantillon.
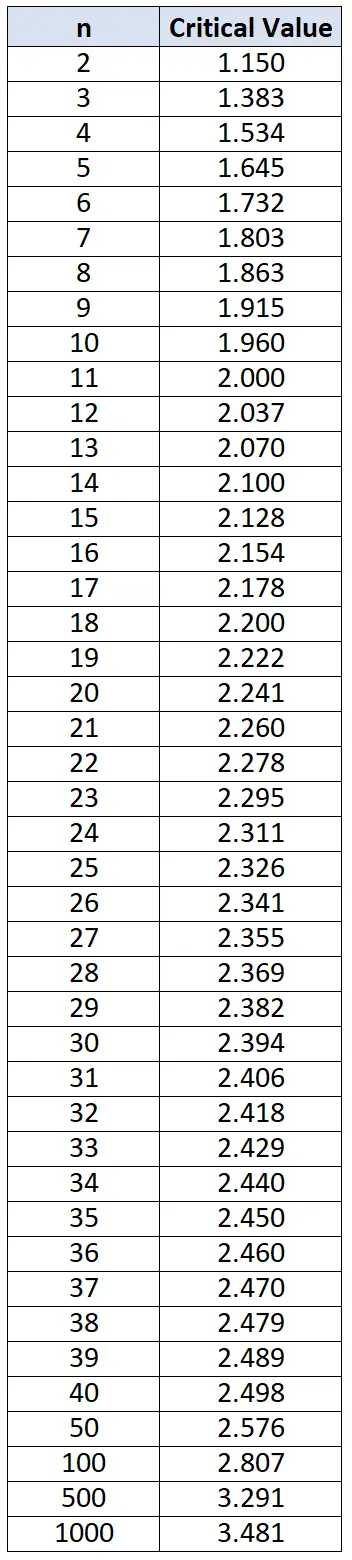
2. Comparez les écarts de chaque valeur individuelle aux valeurs critiques du tableau des critères de Chauvenet ci-dessous. Pour les valeurs de données individuelles présentant des écarts supérieurs à ceux trouvés dans le tableau, déclarez ces valeurs de données comme valeurs aberrantes.
Le critère de Chauvenet : un exemple
Supposons que nous ayons l’ensemble de données suivant de 15 valeurs :
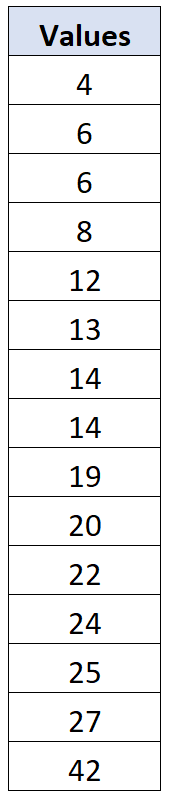
La moyenne de l’échantillon pour cet ensemble de données est x = 17,067 et l’écart type de l’échantillon est s = 10,096 . Pour chaque valeur de données individuelle, nous pouvons calculer son écart comme suit :
Déviation = |x je – x | /s
Par exemple:
- La première valeur de données aurait un écart de |4 – 17,067| / 10,096 = 1,294 .
- La première valeur de données aurait un écart de |6 – 17,067| / 10,096 = 1,096 .
Et ainsi de suite.
Nous pouvons utiliser la même formule pour calculer l’écart de chaque valeur de données individuelle :
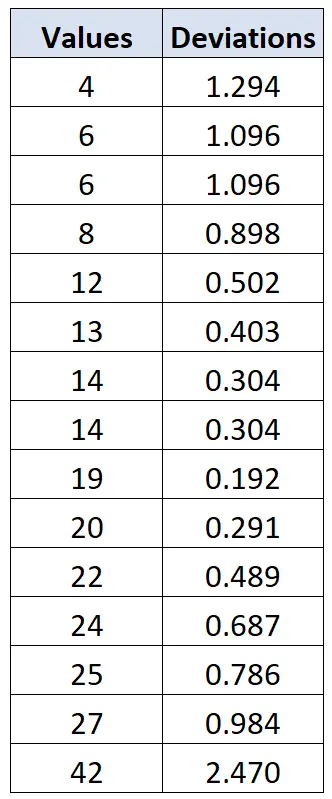
On peut alors se référer au tableau des critères de Chauvenet et constater que la valeur critique qui correspond à une taille d’échantillon de n=15 est 2,128 . Ainsi, toute valeur présentant un écart supérieur à 2,128 peut être considérée comme une valeur aberrante.
Il s’avère que la valeur 42 présente un écart supérieur à 2,128 :
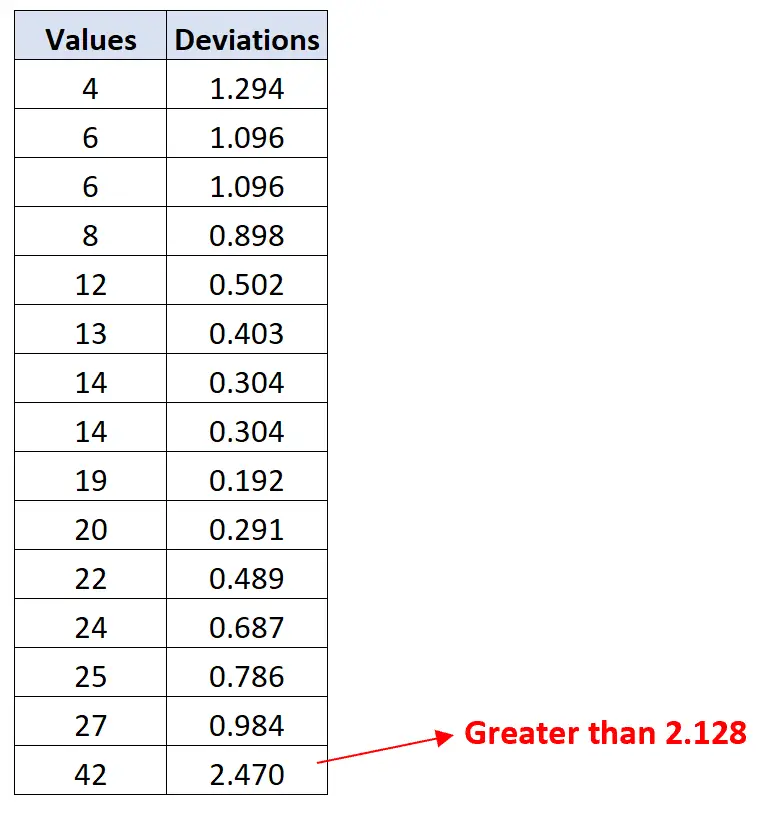
Ainsi, la valeur 42 est la seule valeur aberrante dans cet ensemble de données.
Précautions concernant l’utilisation du critère de Chauvenet
Le critère de Chauvenet part de l’hypothèse que les valeurs d’un ensemble de données sontnormalement distribuées . Si cette hypothèse n’est pas satisfaite, l’utilisation du critère de Chauvenet pour identifier les valeurs aberrantes n’est probablement pas valide.
Si vous utilisez cette méthode et constatez qu’une valeur est aberrante, vous devez d’abord vérifier que la valeur ne résulte pas d’une erreur de saisie de données. Parfois, les données sont simplement mal saisies.
Si la valeur est réellement aberrante, vous pouvez choisir de la supprimer si elle aura un impact significatif sur votre analyse globale. Assurez-vous simplement de mentionner que vous avez supprimé une valeur aberrante lorsque vous signalez vos résultats.
De plus, cette méthode ne doit être utilisée qu’une seule fois sur un ensemble de données donné. Par exemple, supposons que nous utilisions ce critère pour identifier la valeur 42 comme valeur aberrante dans l’exemple précédent et supprimions cette valeur de l’ensemble de données.
Nous ne devrions alors pas recalculer la moyenne de l’échantillon et l’écart type de l’échantillon et calculer à nouveau les écarts pour trouver davantage de valeurs aberrantes.
