Variation intra-groupe ou entre groupes dans l’ANOVA
Une ANOVA unidirectionnelle est utilisée pour déterminer si les moyennes de trois groupes indépendants ou plus sont égales ou non.
Une ANOVA unidirectionnelle utilise les hypothèses nulles et alternatives suivantes :
- H 0 : Toutes les moyennes de groupe sont égales.
- H A : Au moins une moyenne de groupe est différente des autres.
Chaque fois que vous effectuez une ANOVA unidirectionnelle, vous vous retrouverez avec un tableau récapitulatif qui ressemble au suivant :
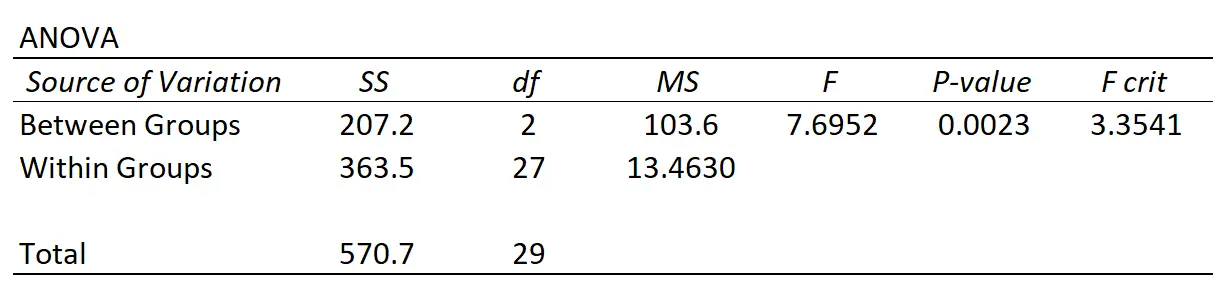
Nous pouvons voir qu’il existe deux sources de variation différentes qu’une ANOVA mesure :
Variation entre groupes : la variation totale entre la moyenne de chaque groupe et la moyenne globale.
Variation intra-groupe : la variation totale des valeurs individuelles dans chaque groupe et leur moyenne de groupe.
Si la variation entre les groupes est élevée par rapport à la variation au sein du groupe, alors la statistique F de l’ANOVA sera plus élevée et la valeur p correspondante sera plus faible, ce qui rend plus probable le rejet de l’hypothèse nulle selon laquelle les moyennes du groupe sont égales.
L’exemple suivant montre comment calculer la variation entre les groupes et la variation au sein du groupe pour une ANOVA unidirectionnelle dans la pratique.
Exemple : calcul de la variation au sein d’un groupe et entre les groupes dans l’ANOVA
Supposons que nous souhaitions déterminer si trois méthodes d’étude différentes conduisent à des notes moyennes différentes aux examens. Pour tester cela, nous recrutons 30 étudiants et en assignons 10 au hasard à chacun pour utiliser une méthode d’étude différente.
Les résultats des examens des étudiants de chaque groupe sont indiqués ci-dessous :
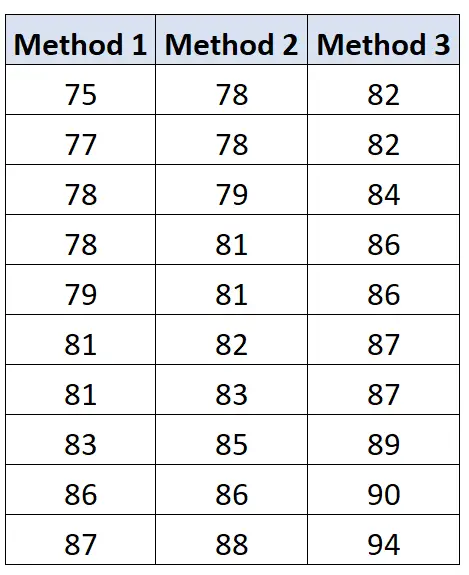
Nous pouvons utiliser la formule suivante pour calculer la variation entre les groupes :
Variation entre groupes = Σn j (X j – X ..) 2
où:
- n j : la taille de l’échantillon du groupe j
- Σ : un symbole qui signifie « somme »
- X j : la moyenne du groupe j
- X .. : la moyenne globale
Pour calculer cette valeur, nous allons d’abord calculer la moyenne de chaque groupe et la moyenne globale :
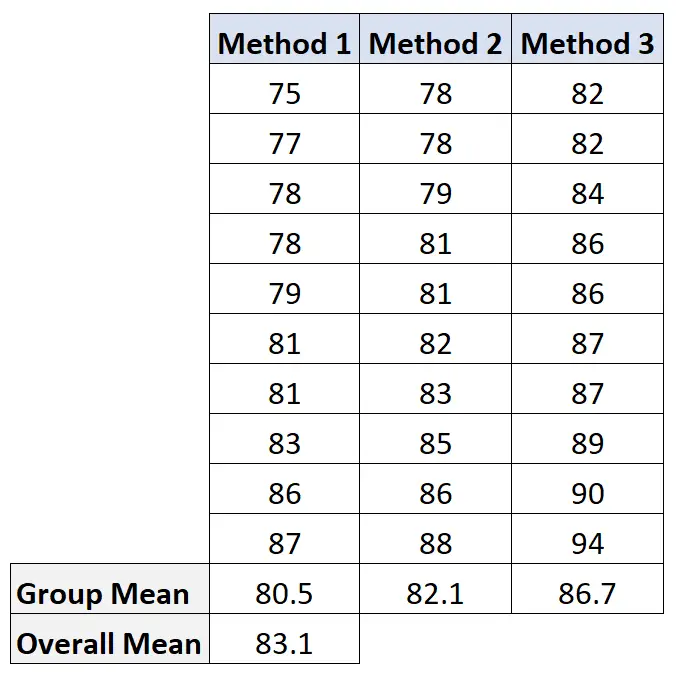
Ensuite, nous calculons la variation entre les groupes comme suit : 10(80,5-83,1) 2 + 10(82,1-83,1) 2 + 10(86,7-83,1) 2 = 207,2 .
Ensuite, nous pouvons utiliser la formule suivante pour calculer la variation au sein du groupe :
Variation intra-groupe : Σ(X ij – X j ) 2
où:
- Σ : un symbole qui signifie « somme »
- X ij : la ième observation du groupe j
- X j : la moyenne du groupe j
Dans notre exemple, nous calculons la variation au sein du groupe comme étant :
Groupe 1 : (75-80,5) 2 + (77-80,5) 2 + (78-80,5) 2 + (78-80,5) 2 + (79-80,5) 2 + (81-80,5) 2 + (81-80,5) 2 + (83-80,5) 2 + (86-80,5) 2 + (87-80,5) 2 = 136,5
Groupe 2 : (78-82,1) 2 + (78-82,1) 2 + (79-82.1) 2 + (81-82.1) 2 + (81-82.1) 2 + (82-82.1) 2 + (83-82.1) 2 + (85-82.1) 2 + (86-82.1) 2 + (88-82,1) 2 = 104,9
Groupe 3 : (82-86,7) 2 + (82-86,7) 2 + (84-86,7) 2 + (86-86,7) 2 + (86-86,7) 2 + (87-86.7) 2 + (87-86.7) 2 + (89-86.7) 2 + (90-86,7) 2 + (94-86,7) 2 = 122,1
Variation au sein du groupe : 136,5 + 104,9 + 122,1 = 363,5
Si nous utilisons un logiciel statistique pour effectuer une ANOVA unidirectionnelle en utilisant cet ensemble de données, nous obtiendrons le tableau ANOVA suivant :
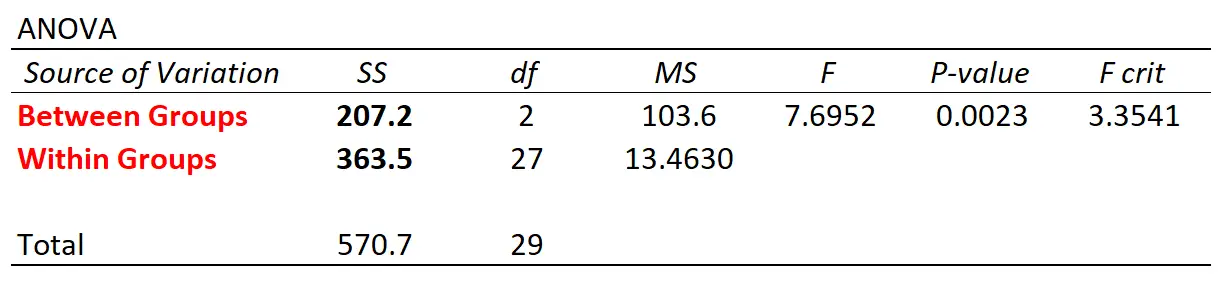
Notez que les valeurs de variation entre les groupes et au sein du groupe correspondent à celles que nous avons calculées manuellement.
La statistique F globale du tableau est un moyen de quantifier le rapport entre la variation entre les groupes et la variation au sein du groupe.
Plus la statistique F est grande, plus la variation entre les moyennes des groupes est grande par rapport à la variation au sein des groupes.
Ainsi, plus la statistique F est grande, plus il est évident qu’il existe une différence entre les moyennes des groupes.
Nous pouvons voir dans cet exemple que la valeur p qui correspond à une statistique F de 7,6952 est .0023 .
Puisque cette valeur est inférieure à α = 0,05, nous rejetons l’hypothèse nulle de l’ANOVA et concluons que les trois techniques d’étude ne conduisent pas au même score à l’examen.
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur les modèles ANOVA :
Introduction à l’ANOVA unidirectionnelle
Comment interpréter la valeur F et la valeur P dans l’ANOVA
Le guide complet : Comment rapporter les résultats de l’ANOVA
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus